Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-30T20:54:19.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Simultaneous direct measurements of concentration and velocity in the Richtmyer–Meshkov instability

Published online by Cambridge University Press:  21 June 2018

Daniel T. Reese Open the ORCID record for Daniel T. Reese [Opens in a new window] ,
Alex M. Ames ,
Chris D. Noble ,
Jason G. Oakley ,
David A. Rothamer  and
Riccardo Bonazza
Daniel T. Reese
Affiliation:
Department of Engineering Physics, University of Wisconsin, Madison, WI 53706, USA
Alex M. Ames
Affiliation:
Department of Engineering Physics, University of Wisconsin, Madison, WI 53706, USA
Chris D. Noble
Affiliation:
Department of Engineering Physics, University of Wisconsin, Madison, WI 53706, USA
Jason G. Oakley
Affiliation:
Department of Engineering Physics, University of Wisconsin, Madison, WI 53706, USA
David A. Rothamer
Affiliation:
Department of Mechanical Engineering, University of Wisconsin, Madison, WI 53706, USA
Riccardo Bonazza
Affiliation:
Department of Engineering Physics, University of Wisconsin, Madison, WI 53706, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

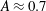The Richtmyer–Meshkov instability (RMI) is experimentally investigated in a vertical shock tube using a broadband initial condition imposed on an interface between a helium–acetone mixture and argon (Atwood number $A\approx 0.7$). In the present work, a shear layer is introduced at the interface to serve as a statistically repeatable, broadband initial condition to the RMI, and the density interface is accelerated by either an 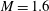$M=1.6$ or 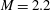$M=2.2$ planar shock wave. The development of the ensuing mixing layer is investigated using simultaneous planar laser-induced fluorescence (PLIF) and particle image velocimetry (PIV). PLIF images are processed to reveal the light-gas mole fraction, while PIV particle image pairs yield corresponding two-component planar velocity results. Field structure and distribution are explored through probability density functions (PDFs), and a decomposition is performed on concentration and velocity results to obtain a mean flow field and define fluctuations. Simultaneous concentration and velocity field measurements allow – for the first time in this regime – experimentally determined turbulence quantities such as Reynolds stresses, turbulent mass-flux velocities and turbulent kinetic energy to be obtained. We show that by the latest times the mixing layer has passed the turbulent threshold, and there is evidence of turbulent mixing occurring sooner for the higher Mach number case. Interface measurements show nonlinear growth with a power-law fit to the thickness data, and that integral measurements of mixing layer thickness are proportional to threshold measurements. Spectral analysis demonstrates the emergence of an inertial range with a slope 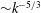${\sim}k^{-5/3}$ when considering both density and velocity effects in planar turbulent kinetic energy (TKE) measurements.

JFM classification

Instability: Instability Instability: Transition to turbulence Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 849 , 25 August 2018 , pp. 541 - 575
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Present address: National Institute of Aerospace, Hampton, VA 23666, USA. Email address for correspondence: [email protected]

References

Anderson, M. H., Puranik, B. P., Oakley, J. G., Brooks, P. W. & Bonazza, R. 2000 Shock tube investigation of hydrodynamic issues related to inertial confinement fusion. Shock Waves 10, 377–387.Google Scholar
Andronov, V. A., Bakhrakh, S. M., Meshkov, E. E., Mokhov, V. N., Nikiforov, V. V., Pevnitskii, A. V. & Tolshmyakov, A. I. 1976 Turbulent mixing at contact surface accelerated by shock waves. Sov. Phys. JETP 44, 424–427.Google Scholar
Arnett, D. 2000 The role of mixing in astrophysics. Astrophys. J. Suppl. Ser. 127 (2), 213–217.Google Scholar
Balakumar, B. J., Orlicz, G. C., Ristorcelli, J. R., Balasubramanian, S., Prestridge, K. P. & Tomkins, C. D. 2012 Turbulent mixing in a Richtmyer–Meshkov fluid layer after reshock: velocity and density statistics. J. Fluid Mech. 696, 67–93.Google Scholar
Balasubramanian, S., Orlicz, G. C. & Prestridge, K. P. 2013 Experimental study of initial condition dependence on turbulent mixing in shock-accelerated Richtmyer–Meshkov fluid layers. J. Turbul. 14 (3), 170–196.Google Scholar
Banerjee, A., Kraft, W. N. & Andrews, M. J. 2010 Detailed measurements of a statistically steady Rayleigh–Taylor mixing layer from small to high Atwood numbers. J. Fluid Mech. 659, 127–190.Google Scholar
Brouillette, M. & Sturtevant, B. 1994 Experiments on the Richtmyer–Meshkov instability: single-scale perturbations on a continuous interface. J. Fluid Mech. 263, 271–292.Google Scholar
Champagne, F. H., Harris, V. G. & Corrsin, S. 1970 Experiments on nearly homogeneous turbulent shear flow. J. Fluid Mech. 41 (01), 81–139.Google Scholar
Cohen, R. H., Dannevik, W. P., Dimits, A. M., Eliason, D. E., Mirin, A. A., Zhou, Y., Porter, D. H. & Woodward, P. R. 2002 Three-dimensional simulation of a Richtmyer–Meshkov instability with a two-scale initial perturbation. Phys. Fluids 14 (10), 3692–3709.Google Scholar
Collins, B. D. & Jacobs, J. W. 2002 PLIF flow visualization and measurements of the Richtmyer–Meshkov instability of an air/SF6 interface. J. Fluid Mech. 464, 113–136.Google Scholar
Cook, A. W., Cabot, W. & Miller, P. L. 2004 The mixing transition in Rayleigh–Taylor instability. J. Fluid Mech. 511, 333–362.Google Scholar
Cook, A. W. & Dimotakis, P. E. 2001 Transition stages of Rayleigh–Taylor instability between miscible fluids. J. Fluid Mech. 443, 69–99.Google Scholar
Dalziel, S. B., Linden, P. F. & Youngs, D. L. 1999 Self-similarity and internal structure of turbulence induced by Rayleigh–Taylor instability. J. Fluid Mech. 399, 1–48.Google Scholar
Dimonte, G. & Schneider, M. 1997 Turbulent Richtmyer–Meshkov instability experiments with strong radiatively driven shocks. Phys. Plasmas 4 (12), 4347–4357.Google Scholar
Dimonte, G. & Schneider, M. 2000 Density ratio dependence of Rayleigh–Taylor mixing for sustained and impulsive acceleration histories. Phys. Fluids 12, 304–321.Google Scholar
Dimotakis, P. E. 2000 The mixing transition in turbulent flows. J. Fluid Mech. 409, 69–98.Google Scholar
Gerashchenko, S. & Prestridge, K. P. 2015 Density and velocity statistics in variable density turbulent mixing. J. Turbul. 16, 1011–1035.Google Scholar
Grinstein, F. F. 2016 Coarse Grained Simulation and Turbulent Mixing. Cambridge University Press.Google Scholar
Grinstein, F. F., Gowardhan, A. A. & Wachtor, A. J. 2011 Simulations of Richtmyer–Meshkov instabilities in planar shock-tube experiments. Phys. Fluids 23 (3), 034106.Google Scholar
Heim, D. M., Jesch, D. & Ghandhi, J. B. 2014 Size-scaling effect on the velocity field of an internal combustion engine, part ii: turbulence characteristics. Intl J. Engine Res. 15 (2), 193–208.Google Scholar
Hill, D. J., Pantano, C. & Pullin, D. I. 2006 Large-eddy simulation and multiscale modelling of a Richtmyer–Meshkov instability with reshock. J. Fluid Mech. 557, 29–61.Google Scholar
Jacobs, J. W., Krivets, V. V., Tsiklashvili, V. & Likhachev, O. A. 2013 Experiments on the Richtmyer–Meshkov instability with an imposed, random initial perturbation. Shock Waves 23 (4), 407–413.Google Scholar
Jones, M. A. & Jacobs, J. W. 1997 A membraneless experiment for the study of Richtmyer–Meshkov instability of a shock-accelerated gas interface. Phys. Fluids 9 (10), 3078–3085.Google Scholar
Kaiser, S. A. & Frank, J. H. 2007 Imaging of dissipative structures in the near field of a turbulent non-premixed jet flame. Proc. Combust. Inst. 31 (1), 1515–1523.Google Scholar
Kane, J., Drake, R. P. & Remington, B. A. 1999 An evaluation of the Richtmyer–Meshkov instability in supernova remnant formation. Astrophys. J. 511 (1), 335–340.Google Scholar
Lindl, J. D., Amendt, P., Berger, R. L., Glendinning, S. G., Glenzer, S. H., Haan, S. W., Kauffman, R. L., Landen, O. L. & Suter, L. J. 2004 The physics basis for ignition using indirect-drive targets on the national ignition facility. Phys. Plasmas 11 (2), 339–491.Google Scholar
Livescu, D. & Ristorcelli, J. R. 2008 Variable-density mixing in buoyancy-driven turbulence. J. Fluid Mech. 605, 145–180.Google Scholar
Marble, F., Hendricks, G. & Zukoski, E. 1987 Progress toward shock enhancement of supersonic combustion processes. In 23rd AIAA, SAE, ASME, and ASEE, Joint Propulsion Conference, San Diego, CA June 29-July 2, pp. 1–8. AIAA.Google Scholar
Mellado, J. P., Sarkar, S. & Zhou, Y. 2005 Large–eddy simulation of Rayleigh–Taylor turbulence with compressible miscible fluids. Phys. Fluids 17, 076101.Google Scholar
Meshkov, E. E. 1970 Instability of a shock wave accelerated interface between two gases. NASA Tech. Transl. 13, 1–14.Google Scholar
Miles, A. R., Blue, B., Edwards, M. J., Greenough, J. A., Hansen, J. F., Robey, H. F., Drake, R. P., Kuranz, C. & Leibrandt, D. R. 2005 Transition to turbulence and effect of initial conditions on three-dimensional compressible mixing in planar blast-wave-driven systems. Phys. Plasmas 12 (5), 056317.Google Scholar
Mohaghar, M., Carter, J., Musci, B., Reilly, D., McFarland, J. & Ranjan, D. 2017 Evaluation of turbulent mixing transition in a shock-driven variable-density flow. J. Fluid Mech. 831, 779–825.Google Scholar
Motl, B., Oakley, J., Ranjan, D., Weber, C., Anderson, M. & Bonazza, R. 2009 Experimental validation of a Richtmyer–Meshkov scaling law over large density ratio and shock strength ranges. Phys. Fluids 21 (12), 126102.Google Scholar
Mueschke, N. J., Andrews, M. J. & Schilling, O. 2006 Experimental characterization of initial conditions and spatio-temporal evolution of a small-Atwood-number Rayleigh–Taylor mixing layer. J. Fluid Mech. 567, 27–63.Google Scholar
Orlicz, G. C., Balasubramanian, S., Vorobieff, P. & Prestridge, K. P. 2015 Mixing transition in a shocked variable-density flow. Phys. Fluids 27 (11), 114102.Google Scholar
Petersen, B. & Ghandhi, J. 2011 High-resolution turbulent scalar field measurements in an optically accessible internal combustion engine. Exp. Fluids 51, 1695–1708.Google Scholar
Pope, S. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Prasad, J. K., Rasheed, A., Kumar, S. & Sturtevant, B. 2000 The late-time development of the Richtmyer–Meshkov instability. Phys. Fluids 12 (8), 2108–2115.Google Scholar
Prestridge, K., Rightley, P. M., Vorobieff, P., Benjamin, R. F. & Kurnit, N. A. 2000 Simultaneous density-field visualization and PIV of a shock-accelerated gas curtain. Exp. Fluids 29, 339–346.Google Scholar
Ramaprabhu, P. & Andrews, M. J. 2004 Experimental investigation of Rayleigh–Taylor mixing at small Atwood numbers. J. Fluid Mech. 502, 233–271.Google Scholar
Reese, D., Oakley, J., Navarro-Nunez, A., Rothamer, D., Weber, C. & Bonazza, R. 2014 Simultaneous concentration and velocity field measurements in a shock-accelerated mixing layer. Exp. Fluids 55, 1823.Google Scholar
Reid, R. C., Prausnitz, J. M. & Poling, B. E. 1987 The Properties of Gases and Liquids. McGraw Hill Book Co.Google Scholar
Richtmyer, R. D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Maths 13 (2), 297–319.Google Scholar
Schilling, O. & Latini, M. 2010 High-order WENO simulations of three-dimensional reshocked Richtmyer–Meshkov instability to late times: dynamics, dependence on initial conditions, and comparisons to experimental data. Acta Math. Sci. 30 (2), 595–620.Google Scholar
Sciacchitano, A., Neal, D. R., Smith, B. L., Warner, S. O., Vlachos, P. P., Wieneke, B. & Scarano, F. 2015 Collaborative framework for piv uncertainty quantification: comparative assessment of methods. Meas. Sci. Technol. 26, 074004.Google Scholar
Taylor, G. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I. Proc. R. Soc. Lond. 201 (1065), 192–196.Google Scholar
Thornber, B., Drikakis, D., Youngs, D. L. & Williams, R. J. R. 2010 The influence of initial conditions on turbulent mixing due to Richtmyer–Meshkov instability. J. Fluid Mech. 654, 99–139.Google Scholar
Vetter, M. & Sturtevant, B. 1995 Experiments on the Richtmyer–Meshkov instability of an air/SF6 interface. Shock Waves 4, 247–252.Google Scholar
Vorobieff, P., Mohamed, N. G., Tomkins, C., Goodenough, C., Marr-Lyon, M. & Benjamin, R. F. 2003 Scaling evolution in shock-induced transition to turbulence. Phys. Rev. E 68 (6), 065301.Google Scholar
Vorobieff, P., Rightley, P. M. & Benjamin, R. F. 1998 Power-law spectra of incipient gas-curtain turbulence. Phys. Rev. Lett. 81, 2240–2243.Google Scholar
Weber, C. R.2012 Turbulent mixing measurements in the Richtmyer–Meshkov instability PhD thesis, University of Wisconsin-Madison.Google Scholar
Weber, C. R., Haehn, N., Oakley, J., Rothamer, D. & Bonazza, R. 2012 Turbulent mixing measurements in the Richtmyer–Meshkov instability. Phys. Fluids 24 (7), 074105.Google Scholar
Weber, C. R., Haehn, N., Oakley, J., Rothamer, D. & Bonazza, R. 2014 An experimental investigation of the turbulent mixing transition in the Richtmyer–Meshkov instability. J. Fluid Mech. 748, 457–487.Google Scholar
Wilson, P. N. & Andrews, M. J. 2002 Spectral measurements of Rayleigh–Taylor mixing at small atwood number. Phys. Fluids 14 (3), 938.Google Scholar
Youngs, D. L. 1994 Numerical simulation of mixing by Rayleigh–Taylor and Richtmyer–Meshkov instabilities. Laser Part. Beams 12 (4), 725–750.Google Scholar
Zhou, Y. 2001 A scaling analysis of turbulent flows driven by Rayleigh–Taylor and Richtmyer–Meshkov instabilities. Phys. Fluids 13 (2), 538–543.Google Scholar