Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T19:26:09.475Z Has data issue: false hasContentIssue false
  • English
  • Français

Simulations of rib-roughened rough-to-smooth turbulent channel flows

Published online by Cambridge University Press:  21 March 2018

Umair Ismail Open the ORCID record for Umair Ismail [Opens in a new window] ,
Tamer A. Zaki Open the ORCID record for Tamer A. Zaki [Opens in a new window]  and
Paul A. Durbin
Umair Ismail*
Affiliation:
Department of Aerospace Engineering, Iowa State University, Ames, IA 50011, USA
Tamer A. Zaki
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
Paul A. Durbin
Affiliation:
Department of Aerospace Engineering, Iowa State University, Ames, IA 50011, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

High-fidelity simulations of turbulent flow through a channel with a rough wall, followed by a smooth wall, demonstrate a high degree of non-equilibrium within the recovery region. In fact, the recovery of all the flow statistics studied is incomplete by the streamwise exit of the computational domain. Above a thin wall layer, turbulence intensities significantly higher than fully developed, smooth-wall levels persist in the developing region. Within the thin wall layer, the profile shapes for turbulence stresses recover very quickly and wall-normal locations of characteristic peaks are established. However, even in this thin layer, complete recovery of magnitudes of turbulence stresses is exceptionally slow. A similar initially swift but eventually incomplete and slow relaxation behaviour is also shown by the skin friction. Between the turbulence shear and streamwise stresses, the turbulence shear stress shows a comparatively quick rate of recovery above a thin wall layer. Over the developing smooth wall, the balance is not merely between fluxes due to pressure and shear stresses. Strong momentum fluxes, which are directly influenced by the upstream roughness size, contribute significantly to this balance. Approximate curve fits estimate the streamwise distance required by the outer peaks of Reynolds stresses to attain near-fully-developed levels at approximately 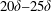$20\unicode[STIX]{x1D6FF}{-}25\unicode[STIX]{x1D6FF}$, with 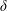$\unicode[STIX]{x1D6FF}$ being the channel half height. An even longer distance, of more than 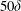$50\unicode[STIX]{x1D6FF}$, might be needed by the mean velocity to approach near-fully-developed magnitudes. Visualizations and correlations show that large-scale eddies that are created above the roughness persist downstream, and sporadically perturb the elongated streaks. These streaks of alternating high and low momentum appear almost instantly after the roughness is removed. The mean flow does not re-establish an equilibrium log layer within the computational domain, and the velocity deficit created by the roughness continues throughout the domain. On the step change in roughness, near the wall, profiles for turbulence kinetic energy dissipation rate, $\unicode[STIX]{x1D716}$, and energy spectra indicate a sharp reduction in energy at small scales. Despite this, reversion towards equilibrium smooth-wall levels is slow, and ultimately incomplete, due to a rather slow adjustment of the turbulence cascade. The non-dimensional roughness height, 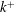$k^{+}$ ranges from 42 to 254 and the friction velocity Reynolds number at the smooth wall, 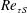$Re_{\unicode[STIX]{x1D70F}S}$, ranges from 284 to 1160 in the various simulations.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 843 , 25 May 2018 , pp. 419 - 449
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andreopoulos, J. & Wood, D. H. 1982 The response of a turbulent boundary layer to a short length of surface roughness. J. Fluid Mech. 118, 143–164.10.1017/S0022112082001001Google Scholar
Antonia, R. A. & Luxton, R. E. 1971 The response of a turbulent boundary layer to a step change in surface roughness. Part 1. Smooth to rough. J. Fluid Mech. 48 (4), 721–761.10.1017/S0022112071001824Google Scholar
Antonia, R. A. & Luxton, R. E. 1972 The response of a turbulent boundary layer to a step change in surface roughness. Part 2. Rough-to-smooth. J. Fluid Mech. 53, 737–757.10.1017/S002211207200045XGoogle Scholar
Ashrafian, A., Andersson, H. I. & Manhart, M. 2004 DNS of turbulent flow in a rod-roughened channel. Intl J. Heat Fluid Flow 25 (3), 373–383.10.1016/j.ijheatfluidflow.2004.02.004Google Scholar
Cheng, H. & Castro, I. P. 2002 Near-wall flow development after a step change in surface roughness. Boundary-Layer Meteorol. 105 (3), 411–432.10.1023/A:1020355306788Google Scholar
Durbin, P. A. & Reif, B. A. P. 2011 Statistical Theory and Modeling for Turbulent Flows. Wiley.Google Scholar
Hanjalic, K. & Launder, B. E. 1972 Fully developed asymmetric flow in a plane channel. J. Fluid Mech. 51, 301–335.10.1017/S0022112072001211Google Scholar
Hanson, R. E. & Ganapathisubramani, B. 2016 Development of turbulent boundary layers past a step change in wall roughness. J. Fluid Mech. 795, 494–523.10.1017/jfm.2016.213Google Scholar
Hill, A. V. 1913 The combinations of haemoglobin with oxygen and with carbon monoxide. I. Biochem. J. 7 (5), 471–480.10.1042/bj0070471Google Scholar
Ikeda, T. & Durbin, P. A.2002 Direct simulations of a rough-wall channel flow. Rep. TF-81, Stanford University, Flow Physics and Computation Division, Dept. of Mechanical Engineering.Google Scholar
Ikeda, T. & Durbin, P. A. 2007 Direct simulations of a rough-wall channel flow. J. Fluid Mech. 571, 235–263.10.1017/S002211200600334XGoogle Scholar
Jacobi, I. & Mckeon, B. J. 2011 New perspectives on the impulsive roughness-perturbation of a turbulent boundary layer. J. Fluid Mech. 677, 179–203.10.1017/jfm.2011.75Google Scholar
Jimnez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36 (1), 173–196.10.1146/annurev.fluid.36.050802.122103Google Scholar
Kim, H., Kline, S. J. & Reynolds, W. C. 1971 The production of turbulence near a smooth wall in a turbulent boundary layer. J. Fluid Mech. 50 (1), 133–160.10.1017/S0022112071002490Google Scholar
Leonardi, S. & Castro, I. P. 2010 Channel flow over large cube roughness: a direct numerical simulation study. J. Fluid Mech. 651, 519–539.10.1017/S002211200999423XGoogle Scholar
Leonardi, S., Orlandi, P., Smalley, R. J., Djenidi, L. & Antonia, R. A. 2003 Direct numerical simulations of turbulent channel flow with transverse square bars on one wall. J. Fluid Mech. 491, 229–238.10.1017/S0022112003005500Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.10.1017/jfm.2012.511Google Scholar
Mehdi, F., Klewicki, J. C. & White, C. M. 2013 Mean force structure and its scaling in rough-wall turbulent boundary layers. J. Fluid Mech. 731, 682–712.10.1017/jfm.2013.385Google Scholar
Miyake, Y., Tsujimoto, K. & Nagai, N. 2002 Numerical simulation of channel flow with a rib-roughened wall. J. Turbul. 3 (35), 1–17.10.1088/1468-5248/3/1/035Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re𝜏 = 590. Phys. Fluids 11 (4), 943–945.10.1063/1.869966Google Scholar
Nagano, Y., Hattori, H. & Houra, T. 2004 DNS of velocity and thermal fields in turbulent channel flow with transverse-rib roughness. Intl J. Heat Fluid Flow 25 (3), 393–403.10.1016/j.ijheatfluidflow.2004.02.011Google Scholar
Nikuradse, J.1933 Laws of flow in rough pipes (in German). VDI-Forsch. 361 (translation in NACA Tech. Rep. 1292 (1950). National Advisory Commission for Aeronautics).Google Scholar
Orlandi, P., Leonardi, S. & Antonia, R. A. 2006 Turbulent channel flow with either transverse or longitudinal roughness elements on one wall. J. Fluid Mech. 561, 279–305.10.1017/S0022112006000723Google Scholar
Pearson, B. R., Elavarasan, R. & Antonia, R. A. 1997 Effect of a short roughness strip on a turbulent boundary layer. Appl. Sci. Res. 59 (1), 61–75.10.1023/A:1000861915585Google Scholar
Perry, A. E., Schofield, W. H. & Joubert, P. N. 1969 Rough wall turbulent boundary layers. J. Fluid Mech. 37 (02), 383–413.10.1017/S0022112069000619Google Scholar
Pierce, C. D. & Moin, P. 2004 Progress-variable approach for large-eddy simulation of non-premixed turbulent combustion. J. Fluid Mech. 504, 73–97.10.1017/S0022112004008213Google Scholar
Raupach, M. R., Antonia, R. A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44 (1), 1–25.10.1115/1.3119492Google Scholar
Squire, D. T., Morrill-Winter, C., Hutchins, N., Schultz, M. P., Klewicki, J. C. & Marusic, I. 2016 Comparison of turbulent boundary layers over smooth and rough surfaces up to high Reynolds numbers. J. Fluid Mech. 795, 210–240.10.1017/jfm.2016.196Google Scholar
Taylor, R. P., Taylor, J. K., Hosni, M. H. & Coleman, H. W. 1993 Relaxation of the turbulent boundary layer after an abrupt change from rough to smooth wall. Trans. ASME: J. Fluids Engng 115, 379–382.Google Scholar
Volino, R. J., Schultz, M. P. & Flack, K. A. 2011 Turbulence structure in boundary layers over periodic two- and three-dimensional roughness. J. Fluid Mech. 676, 172–190.10.1017/S0022112011000383Google Scholar
Wallace, J. M. 2016 Quadrant analysis in turbulence research: history and evolution. Annu. Rev. Fluid Mech. 48, 131–158.10.1146/annurev-fluid-122414-034550Google Scholar
Wallace, J. M., Eckelmann, H. & Brodkey, R. S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54 (1), 39–48.10.1017/S0022112072000515Google Scholar
Wei, T., Fife, P., Klewicki, J. & McMurtry, P. 2005 Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.10.1017/S0022112004001958Google Scholar