Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-12-01T03:41:46.618Z Has data issue: false hasContentIssue false
  • English
  • Français

Simulations of natural transition in viscoelastic channel flow

Published online by Cambridge University Press:  05 May 2017

Sang Jin Lee  and
Tamer A. Zaki Open the ORCID record for Tamer A. Zaki [Opens in a new window]
Sang Jin Lee
Affiliation:
Department of Mechanical Engineering, Imperial College London, London SW7 2AZ, UK Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
Tamer A. Zaki*
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Orderly, or natural, transition to turbulence in dilute polymeric channel flow is studied using direct numerical simulations of a FENE-P fluid. Three Weissenberg numbers are simulated and contrasted to a reference Newtonian configuration. The computations start from infinitesimally small Tollmien–Schlichting (TS) waves and track the development of the instability from the early linear stages through nonlinear amplification, secondary instability and full breakdown to turbulence. At the lowest elasticity, the primary TS wave is more unstable than the Newtonian counterpart, and its secondary instability involves the generation of 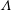$\unicode[STIX]{x1D6EC}$-structures which are narrower in the span. These subsequently lead to the formation of hairpin packets and ultimately breakdown to turbulence. Despite the destabilizing influence of weak elasticity, and the resulting early transition to turbulence, the final state is a drag-reduced turbulent flow. At the intermediate elasticity, the growth rate of the primary TS wave matches the Newtonian value. However, unlike the Newtonian instability mode which reaches a saturated equilibrium condition, the instability in the polymeric flow reaches a periodic state where its energy undergoes cyclical amplification and decay. The spanwise size of the secondary instability in this case is commensurate with the Newtonian 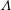$\unicode[STIX]{x1D6EC}$-structures, and the extent of drag reduction in the final turbulent state is enhanced relative to the lower elasticity condition. At the highest elasticity, the exponential growth rate of the TS wave is weaker than the Newtonian flow and, as a result, the early linear stage is prolonged. In addition, the magnitude of the saturated TS wave is appreciably lower than the other conditions. The secondary instability is also much wider in the span, with weaker ejection and without hairpin packets. Instead, streamwise-elongated streaks are formed and break down to turbulence via secondary instability. The final state is a high-drag-reduction flow, which approaches the Virk asymptote.

JFM classification

Non-Newtonian Flows: Non-Newtonian Flows Instability: Transition to turbulence Non-Newtonian Flows: Viscoelasticity
Type
Papers
Information
Journal of Fluid Mechanics , Volume 820 , 10 June 2017 , pp. 232 - 262
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agarwal, A., Brandt, L. & Zaki, T. A. 2014 Linear and nonlinear evolution of a localised disturbance in polymeric channel flow. J. Fluid Mech. 760, 278–303.CrossRefGoogle Scholar
Agarwal, A., Brandt, L. & Zaki, T. A. 2015 Transition to turbulence in viscoelastic channel flow. In IUTAM ABCM Symposium on Laminar Turbulent Transition, Proc. IUTAM 14 , pp. 519–526.Google Scholar
Atalik, K. & Keunings, R. 2002 Non-linear temporal stability analysis of viscoelastic plane channel flows using a fully-spectral method. J. Non-Newtonian Fluid Mech. 102, 299–319.CrossRefGoogle Scholar
Chilcott, N. D. & Rallison, J. M. 1988 Creeping flow of dilute polymer solution past cylinders and spheres. J. Non-Newtonian Fluid Mech. 29, 381–432.CrossRefGoogle Scholar
Cruz, D. O. A., Pinho, F. T. & Oliveira, P. J. 2005 Analytical solutions for fully developed laminar flow of some viscoelastic liquids with a Newtonian solvent contribution. J. Non-Newtonian Fluid Mech. 132, 28–35.CrossRefGoogle Scholar
Dimitropoulos, C. D., Dubief, Y., Shaqfeh, E. S. G., Moin, P. & Lele, S. K. 2005 Direct numerical simulation of polymer-induced drag reduction in turbulent boundary layer flow. Phys. Fluids 17, 011705.CrossRefGoogle Scholar
Dimitropoulos, C. D., Sureshkumar, R. & Beris, A. N. 1998 Direct numerical simulation of viscoelastic turbulent channel flow exhibiting drag reduction: effect of the variation of rheological parameters. J. Non-Newtonian Fluid Mech. 79, 433–468.CrossRefGoogle Scholar
Dubief, Y., Terrapon, V. E. & Soria, J. 2013 On the mechanism of elasto-inertial turbulence. Phys. Fluids 25, 110817.CrossRefGoogle ScholarPubMed
Dubief, Y., Terrapon, V. E., White, C. M., Shaqfeh, E. S. G., Moin, P. & Lele, S. K. 2005 New answers on the interaction between polymers and vortices in turbulent flows. Flow Turbul. Combust. 74, 311–329.CrossRefGoogle Scholar
Dubief, Y., White, C. M., Terrapon, V. E., Shaqfeh, E. S. G., Moin, P. & Lele, S. K. 2004 On the coherent drag-reducing and turbulence-enhancing behaviour of polymers in wall flows. J. Fluid Mech. 514, 271–280.CrossRefGoogle Scholar
Fattal, R. & Kupferman, R. 2005 Time-dependent simulation of viscoelastic flows at high Weissenberg number using the log-conformation representation. J. Non-Newtonian Fluid Mech. 126, 23–37.CrossRefGoogle Scholar
Hack, M. J. P. & Zaki, T. A. 2014 Streak instabilities in boundary layers beneath free-stream turbulence. J. Fluid Mech. 741, 280–315.CrossRefGoogle Scholar
Herbert, T. 1988 Secondary instability of boundary layers. Annu. Rev. Fluid Mech. 20, 487–526.CrossRefGoogle Scholar
Ho, T. C. & Denn, M. M. 1977 Stability of plane Poiseuille flow of a highly elastic liquid. J. Non-Newtonian Fluid Mech. 3, 179–195.CrossRefGoogle Scholar
Hoda, N., Jovanovic, M. R. & Kumar, S. 2008 Energy amplification in channel flows of viscoelastic fluids. J. Fluid Mech. 601, 407–424.CrossRefGoogle Scholar
Hoda, N., Jovanović, M. R. & Kumar, S. 2009 Frequency responses of streamwise-constant perturbations in channel flows of Oldroyd-B fluids. J. Fluid Mech. 625, 411–434.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Kim, K., Adrian, R. J., Balachandar, S. & Sureshkumar, R. 2008 Dynamics of hairpin vortices and polymer-induced turbulent drag reduction. Phys. Rev. Lett. 100, 134504.CrossRefGoogle ScholarPubMed
Kim, K., Li, C.-F., Sureshkumar, R., Balachandar, S. & Adrian, R. J. 2007 Effects of polymer stresses on eddy structures in drag-reduced turbulent channel flow. J. Fluid Mech. 584, 281–299.CrossRefGoogle Scholar
Kim, K. & Sureshkumar, R. 2013 Spatiotemporal evolution of hairpin eddies, Reynolds stress, and polymer torque in polymer drag-reduced turbulent channel flows. Phys. Rev. E 87, 063002.Google ScholarPubMed
Klebanoff, P. S., Tidstrom, K. D. & Sargent, L. M. 1962 The three-dimensional nature of boundary-layer instability. J. Fluid Mech. 12, 1–42.CrossRefGoogle Scholar
Kleiser, L. & Zang, T. A. 1991 Numerical simulation of transition in wall-bounded shear flows. Annu. Rev. Fluid Mech. 23, 495–537.CrossRefGoogle Scholar
Landau, L. D. 1944 On the problem of turbulence. Dokl. Akad. Nauk SSSR 44, 311–314.Google Scholar
Larson, R. G. 1992 Instabilities in viscoelastic flows. Rheol. Acta 31, 213–263.CrossRefGoogle Scholar
Li, C.-F., Sureshkumar, R. & Khomami, B. 2006 Influence of rheological parameters on polymer induced turbulent drag reduction. J. Non-Newtonian Fluid Mech. 140, 23–40.CrossRefGoogle Scholar
Min, T., Yoo, J. Y. & Choi, H. 2001 Effect of spatial discretization schemes on numerical solutions of viscoelastic fluid flows. J. Non-Newtonian Fluid Mech. 100, 27–47.CrossRefGoogle Scholar
Min, T., Yoo, J. Y., Choi, H. & Joseph, D. D. 2003 Drag reduction by polymer additives in a turbulent channel flow. J. Fluid Mech. 486, 213–238.CrossRefGoogle Scholar
Nishioka, M., Iida, S. & Ichikawa, Y. 1975 An experimental investigation of the stability of plane Poiseuille flow. J. Fluid Mech. 72, 731–751.CrossRefGoogle Scholar
Orszag, S. A. & Patera, A. T. 1983 Secondary instability of wall-bounded shear flows. J. Fluid Mech. 128, 347–385.CrossRefGoogle Scholar
Page, J. & Zaki, T. A. 2014 Streak evolution in viscoelastic Couette flow. J. Fluid Mech. 742, 520–551.CrossRefGoogle Scholar
Page, J. & Zaki, T. A. 2015 The dynamics of spanwise vorticity perturbations in homogeneous viscoelastic shear flow. J. Fluid Mech. 777, 327–363.CrossRefGoogle Scholar
Porteous, K. C. & Denn, M. M. 1972 Linear stability of plane Poiseuille flow of viscoelastic liquids. Trans. Soc. Rheol. 16 (2), 295–308.CrossRefGoogle Scholar
Rosenfeld, M., Kwak, D. & Vinokur, M. 1991 A fractional step solution method for the unsteady incompressible Navier–Stokes equations in generalized coordinate systems. J. Comput. Phys. 94, 102–137.CrossRefGoogle Scholar
Sadanandan, B. & Sureshkumar, R. 2002 Viscoelastic effects on the stability of wall-bounded shear flows. Phys. Fluids 14 (1), 41–48.CrossRefGoogle Scholar
Samanta, D. S., Dubief, Y., Holzner, H., Schäfer, C., Morozov, A. N., Wagner, C. & Hof, B. 2013 Elasto-inertial turbulence. Proc. Natl Acad. Sci. USA 110, 10557–10562.CrossRefGoogle ScholarPubMed
Sandham, N. D. & Kleiser, L. 1992 The late stages of transition to turbulence in channel flow. J. Fluid Mech. 245, 319–348.CrossRefGoogle Scholar
Sayadi, T., Hamman, C. W. & Moin, P. 2013 Direct numerical simulation of complete H-type and K-type transitions with implications for the dynamics of turbulent boundary layers. J. Fluid Mech. 724, 480–509.CrossRefGoogle Scholar
Schlichting, H.1933 Zur Entstehung der Turbulenz bei der Plattenströmung. Nach. Ges. Wiss. Gottingen, Math.-Phys. Klasse. 181–208.Google Scholar
Schubauer, G. B. & Skramstad, H. K. 1947 Laminar boundary layer oscillations and stability of laminar flow. J. Aero. Sci. 14 (2), 69–78.Google Scholar
Shu, C.-W. 2009 High order weighted essentially nonoscillatory schemes for convection dominated problems. SIAM Rev. 51 (1), 82–126.CrossRefGoogle Scholar
Stuart, J. T. 1958 On the non-linear mechanics of hydrodynamic stability. J. Fluid Mech. 4, 1–21.CrossRefGoogle Scholar
Terrapon, V. E., Dubief, Y. & Soria, J. 2014 On the role of pressure in elasto-inertial turbulence. J. Turbul. 16 (1), 26–43.CrossRefGoogle Scholar
Tollmien, W.1929 Über die Entstehung der Turbulenz. 1. Mitteilung. Nachr. Ges. Wiss. Gottingen, Math.-Phys. Klasse. 21–44. (Translation in Tollmien, W. 1931 NACA Tech. Rep. TM-609).CrossRefGoogle Scholar
Vaithianathan, T. & Collins, L. R. 2003 Numerical approach to simulating turbulent flow of a viscoelastic polymer solution. J. Comput. Phys. 187, 1–21.CrossRefGoogle Scholar
Vaithianathan, T., Robert, A., Brasseur, J. G. & Collins, L. R. 2006 An improved algorithm for simulating three-dimensional, viscoelastic turbulence. J. Non-Newtonian Fluid Mech. 140, 3–22.CrossRefGoogle Scholar
Vaughan, N. J. & Zaki, T. A. 2011 Stability of zero-pressure-gradient boundary layer distorted by unsteady Klebanoff streaks. J. Fluid Mech. 681, 116–153.CrossRefGoogle Scholar
Virk, P. S. & Mickley, H. S. 1970 The ultimate asymptote and mean flow structures in Tom’s phenomenon. Trans. ASME E: J. Appl. Mech. 37, 488–493.CrossRefGoogle Scholar
Warholic, M. D., Massah, H. & Hanratty, T. J. 1999 Influence of drag-reducing polymers on turbulence: effects of Reynolds number, concentration and mixing. Exp. Fluids 27, 461–471.CrossRefGoogle Scholar
White, F. M. 2006 Viscous Fluid Flow, 3rd edn. McGraw-Hill.Google Scholar
Zaki, T. A. 2013 From streaks to spots and on to turbulence: exploring the dynamics of boundary layer transition. Flow Turbul. Combust. 91, 451–473.CrossRefGoogle Scholar
Zhang, M., Lashgari, I., Zaki, T. A. & Brandt, L. 2013 Linear stability analysis of channel flow of viscoelastic Oldroyd-B and FENE-P fluids. J. Fluid Mech. 737, 249–279.CrossRefGoogle Scholar