Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T16:47:56.889Z Has data issue: false hasContentIssue false
  • English
  • Français

Simulations of a double-diffusive interface in the diffusive convection regime

Published online by Cambridge University Press:  14 September 2012

J. R. Carpenter ,
T. Sommer  and
A. Wüest
J. R. Carpenter
Affiliation:
EAWAG Swiss Federal Institute of Aquatic Science and Technology, Surface Waters – Research and Management, Kastanienbaum, CH-6047, Switzerland
T. Sommer
Affiliation:
EAWAG Swiss Federal Institute of Aquatic Science and Technology, Surface Waters – Research and Management, Kastanienbaum, CH-6047, Switzerland Institute of Biogeochemistry and Pollutant Dynamics, Environmental Sciences, ETH, Zürich, CH-8092, Switzerland
A. Wüest
Affiliation:
EAWAG Swiss Federal Institute of Aquatic Science and Technology, Surface Waters – Research and Management, Kastanienbaum, CH-6047, Switzerland Institute of Biogeochemistry and Pollutant Dynamics, Environmental Sciences, ETH, Zürich, CH-8092, Switzerland Physics of Aquatic Systems Laboratory, ENAC, EPFL, Lausanne, CH-1015, Switzerland
Get access Rights & Permissions [Opens in a new window]

Abstract

Three-dimensional direct numerical simulations are performed that give us an in-depth account of the evolution and structure of the double-diffusive interface. We examine the diffusive convection regime, which, in the oceanographically relevant case, consists of relatively cold fresh water above warm salty water. 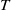A ‘double-boundary-layer’ structure is found in all of the simulations, in which the temperature () interface has a greater thickness than the salinity (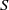) interface. Therefore, thin gravitationally unstable boundary layers are maintained at the edges of the diffusive interface. The 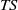-interface thickness ratio is found to scale with the diffusivity ratio in a consistent manner once the shear across the boundary layers is accounted for. The turbulence present in the mixed layers is not able to penetrate the stable stratification of the interface core, and the 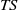-fluxes through the core are given by their molecular diffusion values. Interface growth in time is found to be determined by molecular diffusion of the 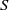-interface, in agreement with a previous theory. The stability of the boundary layers is also considered, where we find boundary layer Rayleigh numbers that are an order of magnitude lower than previously assumed.

JFM classification

Convection: Double diffusive convection Geophysical and Geological Flows: Ocean processes Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 711 , 25 November 2012 , pp. 411 - 436
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Baines, P. G. & Gill, A. 1969 On thermohaline convection with linear gradients. J. Fluid Mech. 34, 289–306.CrossRefGoogle Scholar
2. Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. J. Fluid Mech. 5, 113–133.CrossRefGoogle Scholar
3. Caro, G. P. 2009 Direct numerical simulations of diffusive staircases in the Arctic. Master’s thesis, Naval Postgraduate School.Google Scholar
4. Carpenter, J. R., Sommer, T. & Wüest, A. 2012 Stability of a double-diffusive interface in the diffusive convection regime. J. Phys. Oceanogr. 42, 840–854.CrossRefGoogle Scholar
5. Crapper, P. F. 1975 Measurements across a diffusive interface. Deep-Sea Res. 22, 537–545.Google Scholar
6. Fernando, H. J. S. 1989 Buoyancy transfer across a diffusive interface. J. Fluid Mech. 209, 1–34.CrossRefGoogle Scholar
7. Grossman, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
8. Hoare, R. A. 1966 Problems of heat transfer in Lake Vanda, a density stratified Antarctic Lake. Nature 210, 787–789.CrossRefGoogle Scholar
9. Howard, L. N. 1964 Convection at high Rayleigh number. In Proc. 11th Intl Cong. Appl. Mech. Springer, pp. 1109–1115.Google Scholar
10. Huppert, H. E. & Sparks, R. S. J. 1984 Double-diffusive convection due to crystallization in magmas. Annu. Rev. Earth Planet. Sci. 12, 11–37.CrossRefGoogle Scholar
11. Kelley, D. E. 1990 Fluxes through diffusive staircases: a new formulation. J. Geophys. Res. 95, 3365–3371.CrossRefGoogle Scholar
12. Kelley, D. E., Fernando, H. J. S., Gargett, A. E., Tanny, J. & Özsoy, E. 2003 The diffusive regime of double-diffusive convection. Prog. Oceanogr. 56, 461–481.CrossRefGoogle Scholar
13. Kimura, T. & Smyth, W. D. 2007 Direct numerical simulation of salt sheets and turbulence in a double-diffusive shear layer. Geophys. Res. Lett. 34, L21610.CrossRefGoogle Scholar
14. Linden, P. F. 2000 Convection in the environment. In Perspectives in Fluid Dynamics (ed. Batchelor, G. K., Moffatt, H. K. & Worster, M. G. ), pp. 289–345. Cambridge University Press.Google Scholar
15. Linden, P. F. & Shirtcliffe, T. G. L. 1978 The diffusive interface in double-diffusive convection. J. Fluid Mech. 87, 417–432.CrossRefGoogle Scholar
16. Marmorino, G. O. & Caldwell, D. R. 1976 Heat and salt transport through a diffusive thermohaline interface. Deep-Sea Res. 23, 59–67.Google Scholar
17. Moin, P. & Mahesh, K. 1998 Direct numerical simulation: a tool in turbulence research. Annu. Rev. Fluid Mech. 30, 539–578.CrossRefGoogle Scholar
18. Molemaker, M. J. & Dijkstra, H. A. 1997 The formation and evolution of a diffusive interface. J. Fluid Mech. 331, 199–229.CrossRefGoogle Scholar
19. Neal, V. T., Neshyba, S. & Denner, W. 1969 Thermal stratification in the Arctic Ocean. Science 166, 373–374.CrossRefGoogle ScholarPubMed
20. Newell, T. A. 1984 Characteristics of a double-diffusive interface at high density stability ratios. J. Fluid Mech. 149, 385–401.CrossRefGoogle Scholar
21. Noguchi, T. & Niino, H. 2010a Multi-layered diffusive convection. Part 1. Spontaneous layer formation. J. Fluid Mech. 651, 443–464.CrossRefGoogle Scholar
22. Noguchi, T. & Niino, H. 2010b Multi-layered diffusive convection. Part 2. Dynamics of layer evolution. J. Fluid Mech. 651, 465–481.CrossRefGoogle Scholar
23. Padman, L. & Dillon, T. M. 1987 Vertical heat fluxes through the Beaufort Sea thermohaline staircase. J. Geophys. Res. 92, 10,799–10,806.Google Scholar
24. Padman, L. & Dillon, T. M. 1989 Thermal microstructure and internal waves in the Canada Basin diffusive staircase. Deep-Sea Res. 36, 531–542.CrossRefGoogle Scholar
25. Sanchez, X. & Roget, E. 2007 Microstructure measurements and heat flux calculations of a triple-diffusive process in a lake within the diffusive layer convection regime. J. Geophys. Res. 112, C02012.Google Scholar
26. Schmid, M., Busbridge, M. & Wüest, A. 2010 Double-diffusive convection in Lake Kivu. Limnol. Oceanogr. 55 (1), 225–238.CrossRefGoogle Scholar
27. Schmid, M., Lorke, A., Dinkel, C., Tanyileke, G. & Wüest, A. 2004 Double-diffusive convection in Lake Nyos, Cameroon. Deep-Sea Res. 51, 1097–1111.CrossRefGoogle Scholar
28. Shirtcliffe, T. G. L. 1973 Transport and profile measurements of the diffusive interface in double diffusive convection with similar diffusivities. J. Fluid Mech. 57, 27–43.CrossRefGoogle Scholar
29. Smyth, W. D. & Moum, J. N. 2000 Length scales of turbulence in stably stratified mixing layers. Phys. Fluids 12 (6), 1327–1342.CrossRefGoogle Scholar
30. Smyth, W. D., Moum, J. N. & Caldwell, D. R. 2001 The efficiency of mixing in turbulent patches: Inferences from direct simulations and microstructure observations. J. Phys. Oceanogr. 31, 1969–1992.2.0.CO;2>CrossRefGoogle Scholar
31. Smyth, W. D., Nash, J. D. & Moum, J. N. 2005 Differential diffusion in breaking Kelvin–Helmholtz billows. J. Phys. Oceanogr. 35, 1004–1022.CrossRefGoogle Scholar
32. Sommer, T., Carpenter, J. R., Schmid, M., Lueck, R. & Wüest, A. 2013 Revisiting microstructure sensor responses with implications for double-diffusive fluxes. J. Atmos. Ocean. Technol. (submitted).CrossRefGoogle Scholar
33. Stamp, A. P., Hughes, G. O., Nokes, R. I. & Griffiths, R. W. 1998 The coupling of waves and convection. J. Fluid Mech. 372, 231–271.CrossRefGoogle Scholar
34. Stern, M. E. 1960 The salt-fountain and thermohaline convection. Tellus 2, 172–175.CrossRefGoogle Scholar
35. Takao, S. & Narusawa, U. 1980 An experimental study of heat and mass transfer across a diffusive interface. Intl J. Heat Mass Transfer 23, 1283–1285.CrossRefGoogle Scholar
36. Timmermans, M.-L., Toole, J., Krishfield, R. & Winsor, P. 2008 Ice-tethered profiler observations of the double-diffusive staircase in the Canada Basin thermocline. J. Geophys. Res. 113, C00A02.Google Scholar
37. Turner, J. S. 1965 The coupled turbulent transports of salt and heat across a sharp density interface. Intl J. Heat Mass Transfer 8, 759–767.CrossRefGoogle Scholar
38. Turner, J. S. 1973 Buoyancy Effects in Fluids. Cambridge University Press.CrossRefGoogle Scholar
39. Turner, J. S., Shirtcliffe, T. G. L. & Brewer, P. G. 1970 Elemental variations of transport coefficients across density interfaces in multiple-diffusive systems. Nature 228, 1083–1084.CrossRefGoogle ScholarPubMed
40. Veronis, G. 1965 On finite amplitude instability in thermohaline convection. J. Mar. Res. 23, 1–17.Google Scholar
41. Winters, K. B. & D’Asaro, E. A. 1996 Diascalar flux and the rate of fluid mixing. J. Fluid Mech. 317, 179–193.CrossRefGoogle Scholar
42. Winters, K. B., Lombard, P. N., Riley, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.CrossRefGoogle Scholar
43. Winters, K. B., MacKinnon, J. A. & Mills, B. 2004 A spectral model for process studies of rotating, density-stratified flows. J. Atmos. Ocean. Technol. 21, 69–94.2.0.CO;2>CrossRefGoogle Scholar
44. Worster, M. G. 2004 Time-dependent fluxes across double-diffusive interfaces. J. Fluid Mech. 505, 287–307.CrossRefGoogle Scholar