Hostname: page-component-f554764f5-246sw Total loading time: 0 Render date: 2025-04-15T20:28:04.489Z Has data issue: false hasContentIssue false
  • English
  • Français

Simulation of turbulent flows with the entropic multirelaxation time lattice Boltzmann method on body-fitted meshes

Published online by Cambridge University Press:  15 June 2018

G. Di Ilio ,
B. Dorschner ,
G. Bella ,
S. Succi  and
I. V. Karlin Open the ORCID record for I. V. Karlin [Opens in a new window]
G. Di Ilio*
Affiliation:
Department of Industrial Engineering, University of Rome ‘Niccolò Cusano’, 00166 Rome, Italy
B. Dorschner
Affiliation:
Aerothermochemistry and Combustion Systems Laboratory, Institute of Energy Technology, Department of Mechanical and Process Engineering, ETH Zurich, 8092 Zurich, Switzerland
G. Bella
Affiliation:
Department of Enterprise Engineering, University of Rome ‘Tor Vergata’, 00133 Rome, Italy
S. Succi
Affiliation:
Istituto Applicazioni Calcolo, CNR, 00185 Rome, Italy Center for Life Nano Science, Istituto Italiano di Tecnologia, 00161 Rome, Italy
I. V. Karlin
Affiliation:
Aerothermochemistry and Combustion Systems Laboratory, Institute of Energy Technology, Department of Mechanical and Process Engineering, ETH Zurich, 8092 Zurich, Switzerland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

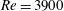We propose a body-fitted mesh approach based on a semi-Lagrangian streaming step combined with an entropy-based collision model. After determining the order of convergence of the method, we analyse the flow past a circular cylinder in the lower subcritical regime, at a Reynolds number $Re=3900$, in order to assess the numerical performances for wall-bounded turbulence. The results are compared to experimental and numerical data available in the literature. Overall, the agreement is satisfactory. By adopting an efficient local refinement strategy together with the enhanced stability features of the entropic model, this method extends the range of applicability of the lattice Boltzmann approach to the solution of realistic fluid dynamics problems, at high Reynolds numbers, involving complex geometries.

JFM classification

Mathematical Foundations: Computational methods Turbulent Flows: Turbulent Flows Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 849 , 25 August 2018 , pp. 35 - 56
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Amati, G., Succi, S. & Benzi, R. 1997 Turbulent channel flow simulations using a coarse-grained extension of the lattice Boltzmann method. Fluid Dyn. Res. 19, 289–302.Google Scholar
Ansumali, S. & Karlin, I. V. 2002 Entropy function approach to the lattice Boltzmann method. J. Stat. Phys. 107, 291–308.Google Scholar
Bangerth, W., Hartmann, R. & Kanschat, G. 2007 deal.II – A general-purpose object-oriented finite element library. ACM Trans. Math. Softw. 33, 24.Google Scholar
Bardow, A., Karlin, I. V. & Gusev, A. A. 2006 General characteristic-based algorithm for off-lattice Boltzmann simulations. Europhys. Lett. 75, 434–440.Google Scholar
Beaudan, P. & Moin, P.1994 Numerical experiments on the flow past a circular cylinder at sub-critical Reynolds number Report No. TF-62, Department of Mechanical Engineering, Stanford University.Google Scholar
Benzi, R., Succi, S. & Vergassola, M. 1992 The lattice Boltzmann equation: theory and applications. Phys. Rep. 222, 145–197.Google Scholar
Boghosian, B. M., Yepez, J., Coveney, P. V. & Wagner, A. J. 2001 Entropic lattice Boltzmann methods. Proc. R. Soc. Lond. A 457, 717–766.Google Scholar
Bouzidi, M., Firdaouss, M. & Lallemand, P. 2001 Momentum transfer of a Boltzmann-lattice fluid with boundaries. Phys. Fluids 13, 3452.Google Scholar
Briscolini, M., Santangelo, P., Succi, S. & Benzi, R. 1994 Extended self-similarity in the numerical simulation of three-dimensional homogeneous flows. Phys. Rev. E 50, R1745(R).Google Scholar
Bösch, F., Chikatamarla, S. S. & Karlin, I. V. 2015 Entropic multirelaxation lattice Boltzmann models for turbulent flows. Phys. Rev. E 92, 043309.Google Scholar
Chen, S. & Doolen, G. D. 1998 Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 30, 329–364.Google Scholar
Chen, H., Kandasamy, S., Orszag, S., Shock, R., Succi, S. & Yakhot, V. 2003 Extended Boltzmann kinetic equation for turbulent flows. Science 301, 633–636.Google Scholar
Corke, T. C. & Thomas, F. O. 2015 Dynamic stall in pitching airfoils: aerodynamic damping and compressibility effects. Annu. Rev. Fluid Mech. 47 (1), 479–505.Google Scholar
Di Ilio, G., Chiappini, D., Ubertini, S., Bella, G. & Succi, S. 2017 Hybrid lattice Boltzmann method on overlapping grids. Phys. Rev. E 95, 013309.Google Scholar
Di Ilio, G., Chiappini, D., Ubertini, S., Bella, G. & Succi, S. 2018 Fluid flow around NACA 0012 airfoil at low-Reynolds numbers with hybrid lattice Boltzmann method. Comput. Fluids 166, 200–208.Google Scholar
Dimotakis, P. E. 2005 Turbulent mixing. Annu. Rev. Fluid Mech. 37, 329–356.Google Scholar
Dong, S., Karniadakis, G. E., Ekmekci, A. & Rockwell, D. 2006 A combined direct numerical simulation-particle image velocimetry study of the turbulent near wake. J. Fluid Mech. 569, 185–207.Google Scholar
Dorschner, B., Bösch, F., Chikatamarla, S. S., Boulouchos, K. & Karlin, I. V. 2016a Entropic multi-relaxation time lattice Boltzmann model for complex flows. J. Fluid Mech. 801, 623–651.Google Scholar
Dorschner, B., Chikatamarla, S. S. & Karlin, I. V. 2017a Entropic multirelaxation-time lattice Boltzmann method for moving and deforming geometries in three dimensions. Phys. Rev. E 95, 063306.Google Scholar
Dorschner, B., Chikatamarla, S. S. & Karlin, I. V. 2017b Transitional flows with the entropic lattice Boltzmann method. J. Fluid Mech. 824, 388–412.Google Scholar
Dorschner, B., Frapolli, N., Chikatamarla, S. S. & Karlin, I. V. 2016b Grid refinement for entropic lattice Boltzmann models. Phys. Rev. E 94, 053311.Google Scholar
Filippova, O. & Hänel, D. 1998 Grid refinement for lattice-BGK models. J. Comput. Phys. 147, 219–228.Google Scholar
Gehrke, M., Janssen, C. F. & Rung, T. 2017 Scrutinizing lattice Boltzmann methods for direct numerical simulations of turbulent channel flows. Comput. Fluids 156, 247–263.Google Scholar
Graham, J. 2017 Rapid distortion of turbulence into an open turbine rotor. J. Fluid Mech. 825, 764–794.Google Scholar
Heroux, M. A., Bartlett, R. A., Howle, V. E., Hoekstra, R. J., Hu, J. J., Kolda, T. G., Lehoucq, R. B., Long, K. R., Pawlowski, R. P., Phipps, E. T. et al. 2005 An overview of the Trilinos project. ACM Trans. Math. Softw. 31, 397–423.Google Scholar
Higuera, F. J. & Jimenez, J. 1989 Boltzmann approach to lattice gas simulations. Europhys. Lett. 9, 663–668.Google Scholar
Higuera, F. J., Succi, S. & Benzi, R. 1989 Lattice gas dynamics with enhanced collisions. Europhys. Lett. 9, 345–349.Google Scholar
Hou, S., Sterling, J., Chen, S. & Doolen, G. D. 1996 A lattice Boltzmann subgrid model for high Reynolds number flows. Fields Inst. Commun. 6, 151–166.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1998 Eddies, stream, and convergence zones in turbulent flows. Center for Turbulence Research Report, CTR-S88, pp. 193–208.Google Scholar
Imamura, T., Suzuki, K., Nakamura, T. & Yoshida, M. 2005 Flow simulation around an airfoil by lattice Boltzmann method on generalized coordinates. AIAA J. 43, 1968–1973.Google Scholar
Jahanshaloo, L., Pouryazdanpanah, E., Azwadi, N. & Sidik, C. 2013 A review on the application of the lattice Boltzmann method for turbulent flow simulation. Numer. Heat Transfer 64, 938–953.Google Scholar
Karlin, I. V., Ansumali, S., Angelis, E. D., Öttinger, H. C. & Succi, S.2003 Entropic lattice Boltzmann method for large scale turbulence simulation. arXiv:cond-mat/0306003 [cond-mat.stat-mech].Google Scholar
Karlin, I. V., Bösch, F. & Chikatamarla, S. S. 2014 Gibbs’ principle for the lattice-kinetic theory of fluid dynamics. Phys. Rev. E 90, 031302(R).Google Scholar
Karlin, I. V., Ferrante, A. & Öttinger, H. C. 1999 Perfect entropy functions of the lattice Boltzmann method. Europhys. Lett. 47, 182–188.Google Scholar
Kravchenko, A. G. & Moin, P. 2000 Numerical studies of flow over a circular cylinder at Re D = 3900. Phys. Fluids 12, 403–417.Google Scholar
Krämer, A., Küllmer, K., Reith, D., Joppich, W. & Foysi, H. 2017 Semi-Lagrangian off-lattice Boltzmann method for weakly compressible flows. Phys. Rev. E 95, 023305.Google Scholar
Lee, T. & Lin, C. L. 2001 A characteristic galerkin method for discrete Boltzmann equation. J. Comput. Phys. 171, 336–356.Google Scholar
Lee, T. & Lin, C. L. 2003 An Eulerian description of the streaming process in the lattice Boltzmann equation. J. Comput. Phys. 185, 445–471.Google Scholar
Li, K., Zhong, C., Zhuo, C. & Cao, J. 2012 Non-body-fitted Cartesian-mesh simulation of highly turbulent flows using multi-relaxation-time lattice Boltzmann method. Comput. Maths Applics. 63, 1481–1496.Google Scholar
Lourenco, L. M. & Shih, C.1993 Characteristics of the plane turbulent near wake of a circular cylinder, a particle image velocimetry study. Published in Beaudan and Moin (1994), data taken from Kravchenko and Moin (2000).Google Scholar
Ma, X., Karamonos, G. S. & Karniadakis, G. E. 2000 Dynamics and low-dimensionality of a turbulent near wake. J. Fluid Mech. 410, 29–65.Google Scholar
Malaspinas, O. & Sagaut, P. 2012 Consistent subgrid scale modelling for lattice Boltzmann methods. J. Fluid Mech. 700, 514–542.Google Scholar
McNamara, G. R. & Zanetti, G. 1988 Use of the Boltzmann equation to simulate lattice-gas automata. Phys. Rev. Lett. 61, 2332–2335.Google Scholar
Min, M. & Lee, T. 2011 A spectral-element discontinuous Galerkin lattice Boltzmann method for nearly incompressible flows. J. Comput. Phys. 230, 245–259.Google Scholar
Namburi, M., Krithivasan, S. & Ansumali, S. 2016 Crystallographic lattice Boltzmann method. Sci. Rep. 6, 27172.Google Scholar
Nathen, P., Gaudlitz, D., Krause, M. J. & Adams, N. A. 2017 On the stability and accuracy of the BGK, MRT and RLB Boltzmann schemes for the simulation of turbulent flows. J. Commun. Comput. Phys. 23, 846–876.Google Scholar
Norberg, C. 1994 An experimental investigation of flow around a circular cylinder: influence of aspect ratio. J. Fluid Mech. 258, 287–316.Google Scholar
Ong, L. & Wallace, J. 1996 The velocity field of the turbulent very near wake of a circular cylinder. Exp. Fluids 20, 441–453.Google Scholar
Orszag, S. A. 1971 Numerical simulation of incompressible flows within simple boundaries: accuracy. J. Fluid Mech. 49, 75–112.Google Scholar
Patel, S. & Lee, T. 2016 A new splitting scheme to the discrete Boltzmann equation for non-ideal gases on non-uniform meshes. J. Comput. Phys. 327, 799–809.Google Scholar
Patil, D. V. 2013 Chapman–Enskog analysis for finite-volume formulation of lattice Boltzmann equation. Physica A 392, 2701–2712.Google Scholar
Patil, D. V. & Lakshmisha, K. N. 2009 Finite volume TVD formulation of lattice Boltzmann simulation on unstructured mesh. J. Comput. Phys. 228, 5262–5279.Google Scholar
Pellerin, N., Leclaire, S. & Reggio, M. 2017 Solving incompressible fluid flows on unstructured meshes with the lattice Boltzmann flux solver. Engng Appl. Comput. Fluid Mech. 11, 310–327.Google Scholar
Peng, G., Xi, H., Duncan, C. & Chou, S. H. 1998 Lattice Boltzmann method on irregular meshes. Phys. Rev. E 58, R4124–R4127.Google Scholar
Peng, G., Xi, H., Duncan, C. & Chou, S. H. 1999 A finite volume scheme for the lattice Boltzmann method on unstructured meshes. Phys. Rev. E 59, 4675–4682.Google Scholar
Rai, M. M. 2010 A computational investigation of the instability of the detached shear layer in the wake of a circular cylinder. J. Fluid Mech. 659, 375–404.Google Scholar
Rajani, B. N., Kandasamy, A. & Majumdar, S. 2016 LES of flow past circular cylinder at Re = 3900. J. Appl. Fluid Mech. 9, 1421–1435.Google Scholar
Rao, P. R. & Schaefer, L. A. 2015 Numerical stability of explicit off-lattice Boltzmann schemes: a comparative study. J. Comput. Phys. 285, 251–264.Google Scholar
Rogallo, R. S. & Moin, P. 1984 Numerical simulation of turbulent flows. Ann. Rev. Fluid Mech. 16, 99–137.Google Scholar
Shu, C., Peng, Y., Zhou, C. F. & Chew, Y. T. 2006 Application of Taylor series expansion and Least-squares-based lattice Boltzmann method to simulate turbulent flows. J. Turbul. 7, N38.Google Scholar
Shu, C., Wang, Y., Teo, C. J. & Wu, J. 2014 Development of lattice Boltzmann flux solver for simulation of incompressible flows. Adv. Appl. Math. Mech. 6, 436–460.Google Scholar
Succi, S. 2001 The Lattice Boltzmann Equation for Fluid Dynamics and Beyond. Clarendon Press.Google Scholar
Succi, S. 2015 Lattice Boltzmann 2038. Europhys. Lett. 109, 50001.Google Scholar
Tseng, Y. H. & Ferziger, J. H. 2003 A ghost-cell immersed boundary method for flow in complex geometry. J. Comput. Phys. 192, 593–623.Google Scholar
Ubertini, S., Bella, G. & Succi, S. 2003 Lattice Boltzmann method on unstructured grids: further developments. Phys. Rev. E 68, 016701.Google Scholar
Ubertini, S., Bella, G. & Succi, S. 2006 Unstructured lattice Boltzmann equation with memory. Math. Comput. Simul. 72, 237–241.Google Scholar
Ubertini, S., Succi, S. & Bella, G. 2004 Lattice Boltzmann schemes without coordinates. Phil. Trans. R. Soc. Lond. A 362, 1763–1771.Google Scholar
Wissink, J. G. & Rodi, W. 2008 Numerical study of the near wake of a circular cylinder. Intl J. Heat Fluid Flow 29, 1060–1070.Google Scholar
Xi, H., Peng, G. & Chou, S. H. 1999 Finite-volume lattice Boltzmann method. Phys. Rev. E 59, 6202–6205.Google Scholar
You, D. & Moin, P. 2006 A dynamic global-coefficient subgrid-scale eddy-viscosity model for large-eddy simulation in complex geometries. Annual Research Briefs, Center for Turbulence Research pp. 41–53.Google Scholar
Zarghami, A., Maghrebi, M. J., Ghasemi, J. & Ubertini, S. 2012 Lattice Boltzmann finite volume formulation with improved stability. Commun. Comput. Phys. 12, 42–64.Google Scholar
Zhu, L., Wang, P. & Guo, Z. 2017 Performance evaluation of the general characteristics based off-lattice Boltzmann scheme and DUGKS for low speed continuum flows. J. Comput. Phys. 333, 227–246.Google Scholar
Zhuo, C., Zhong, C., Li, K., Xiong, S., Chen, X. & Cao, J. 2010 Application of lattice Boltzmann method to simulation of compressible turbulent flow. Commun. Comput. Phys. 8, 1208–1223.Google Scholar