Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Guan, Geng
Ying, Yuxiang
and
Nie, Deming
2020.
Study on the behavior of a light sphere rising in a square tube using the lattice Boltzmann method.
Journal of Physics: Conference Series,
Vol. 1707,
Issue. 1,
p.
012013.
Guan, Geng
Ying, Yuxiang
and
Nie, Deming
2021.
Sedimentation of two unequal spheres in a square tube at low Reynolds numbers.
IOP Conference Series: Earth and Environmental Science,
Vol. 692,
Issue. 4,
p.
042033.
Yang, Sensen
Tu, Chengxu
Dai, Minglu
Ge, Xianfu
Xu, Rongjun
Gao, Xiaoyan
and
Bao, Fubing
2021.
Sedimentation of Two Side-by-Side Heavy Particles of Different Density in a Shear-Thinning Fluid with Viscoelastic Properties.
Applied Sciences,
Vol. 11,
Issue. 15,
p.
7113.
Lallemand, Pierre
Luo, Li-Shi
Krafczyk, Manfred
and
Yong, Wen-An
2021.
The lattice Boltzmann method for nearly incompressible flows.
Journal of Computational Physics,
Vol. 431,
Issue. ,
p.
109713.
Nie, Deming
Guan, Geng
and
Lin, Jianzhong
2021.
Interaction between two unequal particles at intermediate Reynolds numbers: A pattern of horizontal oscillatory motion.
Physical Review E,
Vol. 103,
Issue. 1,
Huang, Lizhong
Du, Jiayou
and
Zhu, Zefei
2021.
Neutrally Buoyant Particle Migration in Poiseuille Flow Driven by Pulsatile Velocity.
Micromachines,
Vol. 12,
Issue. 9,
p.
1075.
Li, Xiaohui
Liu, Guodong
Zhao, Junnan
Yin, Xiaolong
and
Lu, Huilin
2022.
IBM-LBM-DEM Study of Two-Particle Sedimentation: Drafting-Kissing-Tumbling and Effects of Particle Reynolds Number and Initial Positions of Particles.
Energies,
Vol. 15,
Issue. 9,
p.
3297.
Huang, Lizhong
Lin, Jianzhong
Wang, Ruijin
and
Shao, Chun
2022.
Inertial migration of soft particles initially evenly spaced along the flow direction in a channel.
Physics of Fluids,
Vol. 34,
Issue. 10,
Chiu, Chia-Lin
Fan, Chia-Ming
and
Chu, Chia-Ren
2022.
Numerical analysis of two spheres falling side by side.
Physics of Fluids,
Vol. 34,
Issue. 7,
Hu, Xiao
Lin, Peifeng
Lin, Jianzhong
Zhu, Zuchao
and
Yu, Zhaosheng
2022.
On the polydisperse particle migration and formation of chains in a square channel flow of non-Newtonian fluids.
Journal of Fluid Mechanics,
Vol. 936,
Issue. ,
Xiao, Yang
Liu, Jieqing
Zhang, Pei
Zhou, Jian
Liang, Dongfang
Wang, Zhihao
Zhang, Taotao
Yuan, Saiyu
and
Tang, Hongwu
2023.
Experimental study of the settling of twin spherical particles released side by side: The impact of particle size, fluid viscosity, initial spacing, and particle density.
International Journal of Sediment Research,
Vol. 38,
Issue. 1,
p.
83.
Nie, Deming
Ying, Yuxiang
Guan, Geng
Lin, Jianzhong
and
Ouyang, Zhenyu
2023.
Two-dimensional study on the motion and interactions of squirmers under gravity in a vertical channel.
Journal of Fluid Mechanics,
Vol. 960,
Issue. ,
Zhou, Huajie
Chen, Wenbo
Xuan, Chengliang
Qin, Zhangrong
and
Wen, Binghai
2023.
Three-dimensional simulation of red blood cell particle sedimentation.
Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science,
Vol. 237,
Issue. 11,
p.
2485.
Liu, Yi
Guo, Yu
Yang, Bo
Pan, Dingyi
Xia, Zhenhua
Yu, Zhaosheng
and
Wang, Lian-Ping
2023.
Three-dimensional sedimentation patterns of two interacting disks in a viscous fluid.
Journal of Fluid Mechanics,
Vol. 960,
Issue. ,
Wei, Mingzhu
Duan, Jinlong
Wang, Xu
and
Zhou, Jifu
2023.
Motion of a solid particle in an ore-lifting riser with transverse vibrations.
Physics of Fluids,
Vol. 35,
Issue. 11,
Huang, Lizhong
Lin, Jianzhong
Wang, Ruijin
and
Shao, Chun
2023.
The variation in wall shear stress induced by a linear train of soft particles in channel flow.
Applied Physics Letters,
Vol. 123,
Issue. 4,
Huang, Lizhong
Shao, Chun
Wang, Ruijin
Du, Jiayou
and
Zhu, Zefei
2023.
Sedimentation of particles with various shapes and orientations in a closed channel using smoothed particle hydrodynamics.
Fluid Dynamics Research,
Vol. 55,
Issue. 4,
p.
045501.
Liu, Jieqing
Xiao, Yang
Liang, Dongfang
Zhang, Pei
Wang, Zhihao
Liu, Jiaming
Zhang, Taotao
and
Zhou, Jian
2024.
Experimental investigation on inter-particle settling dynamics of multiple spherical particles released side by side at intermediate Reynolds numbers.
Physics of Fluids,
Vol. 36,
Issue. 3,
Wei, Mingzhu
Duan, Jinlong
Wang, Xu
and
Zhou, Jifu
2024.
Simulation of a coarse solid sphere settling in a riser with transverse vibrations.
Physics of Fluids,
Vol. 36,
Issue. 3,
Nie, Deming
Wang, Jingwen
Li, Siwen
and
Lin, Jianzhong
2024.
Freely rising or falling of a sphere in a square tube at intermediate Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 1000,
Issue. ,
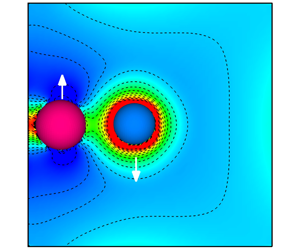
 $0.8\leqslant Re_{T}\leqslant 17.3$ based on the terminal settling velocity. The sedimentation of spheres with different densities is dynamically more complex than that of identical spheres. At high Ga the spheres oscillate in the centreline plane of the tube, where they are initially released from rest. By contrast, the spheres move to the diagonal or reverse–diagonal plane of the tube at low Ga, reaching a steady or periodic state depending on the density difference between them. A phase diagram illustrates the transitions between different sedimentation behaviours depending on Ga and the density difference. A possible mechanism for these behaviours is also presented. Furthermore, we compare two-dimensional (2-D) and three-dimensional computations for our system to attain a better understanding of the hydrodynamic interactions between two unequal spheres at low but finite Reynolds number. Comparing relative trajectories, periods of oscillation and flow features shows that 2-D circular cylinders oscillate much more strongly and frequently than spheres under the same flow conditions. In particular, spheres do not have the discontinuity in period that arises in the 2-D case from the change in rotation sign of a heavy particle.
$0.8\leqslant Re_{T}\leqslant 17.3$ based on the terminal settling velocity. The sedimentation of spheres with different densities is dynamically more complex than that of identical spheres. At high Ga the spheres oscillate in the centreline plane of the tube, where they are initially released from rest. By contrast, the spheres move to the diagonal or reverse–diagonal plane of the tube at low Ga, reaching a steady or periodic state depending on the density difference between them. A phase diagram illustrates the transitions between different sedimentation behaviours depending on Ga and the density difference. A possible mechanism for these behaviours is also presented. Furthermore, we compare two-dimensional (2-D) and three-dimensional computations for our system to attain a better understanding of the hydrodynamic interactions between two unequal spheres at low but finite Reynolds number. Comparing relative trajectories, periods of oscillation and flow features shows that 2-D circular cylinders oscillate much more strongly and frequently than spheres under the same flow conditions. In particular, spheres do not have the discontinuity in period that arises in the 2-D case from the change in rotation sign of a heavy particle.

