Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T01:46:11.675Z Has data issue: false hasContentIssue false
  • English
  • Français

Simulation of air–water interfacial mass transfer driven by high-intensity isotropic turbulence

Published online by Cambridge University Press:  07 December 2018

H. Herlina Open the ORCID record for H. Herlina [Opens in a new window]  and
J. G. Wissink Open the ORCID record for J. G. Wissink [Opens in a new window]
H. Herlina*
Affiliation:
Institute for Hydromechanics, Karlsruhe Institute of Technology, Kaiserstrasse 12, 76131 Karlsruhe, Germany
J. G. Wissink
Affiliation:
Department of Mechanical and Aerospace Engineering, Brunel University London, Kingston Lane, Uxbridge UB8 3PH, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Previous direct numerical simulations (DNS) of mass transfer across the air–water interface have been limited to low-intensity turbulent flow with turbulent Reynolds numbers of 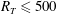$R_{T}\leqslant 500$. This paper presents the first DNS of low-diffusivity interfacial mass transfer across a clean surface driven by high-intensity (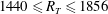$1440\leqslant R_{T}\leqslant 1856$) isotropic turbulent flow diffusing from below. The detailed results, presented here for Schmidt numbers 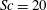$Sc=20$ and 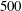$500$, support the validity of theoretical scaling laws and existing experimental data obtained at high 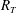$R_{T}$. In the DNS, to properly resolve the turbulent flow and the scalar transport at 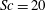$Sc=20$, up to 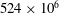$524\times 10^{6}$ grid points were needed, while 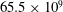$65.5\times 10^{9}$ grid points were required to resolve the scalar transport at 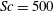$Sc=500$, which is typical for oxygen in water. Compared to the low-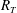$R_{T}$ simulations, where turbulent mass flux is dominated by large eddies, in the present high-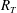$R_{T}$ simulation the contribution of small eddies to the turbulent mass flux was confirmed to increase significantly. Consequently, the normalised mass transfer velocity was found to agree with the 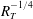$R_{T}^{-1/4}$ scaling, as opposed to the 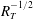$R_{T}^{-1/2}$ scaling that is typical for low-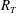$R_{T}$ simulations. At constant 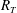$R_{T}$, the present results show that the mass transfer velocity 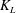$K_{L}$ scales with 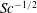$Sc^{-1/2}$, which is identical to the scaling found in the large-eddy regime for 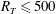$R_{T}\leqslant 500$. As previously found for a no-slip interface, also for a shear-free interface the critical 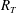$R_{T}$ separating the large- from the small-eddy regime was confirmed to be approximately 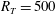$R_{T}=500$.

JFM classification

Geophysical and Geological Flows: Air/sea interactions Turbulent Flows: Isotropic turbulence Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 860 , 10 February 2019 , pp. 419 - 440
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atmane, M. A. & George, J. 2002 Gas transfer across a zero-shear surface: a local approach. In Gas Transfer at Water Surfaces, Geophysics Monograph, vol. 127, pp. 255–259. American Geophysical Union (AGU).Google Scholar
Banerjee, S., Scott, D. S. & Rhodes, E. 1968 Mass transfer to falling wavy liquid films in turbulent flow. Ind. Engng Chem. Fundam. 7 (1), 22–27.Google Scholar
Bodart, J., Cazalbou, J. B. & Joly, L. 2010 Direct numerical simulation of unsheared turbulence diffusing towards a free-slip or no-slip surface. J. Turbul. 11, N48.Google Scholar
Brumley, B. H. & Jirka, G. H. 1987 Near-surface turbulence in a grid-stirred tank. J. Fluid Mech. 183, 235–263.Google Scholar
Brumley, B. H. & Jirka, G. H. 1988 Air–water transfer of slightly soluble gases: turbulence interfacial processes and conceptual models. Physico-Chem. Hydrodyn. 10 (3), 295–319.Google Scholar
Chu, C. R. & Jirka, G. H. 1992 Turbulent gas flux measurements below the air–water interface of a grid-stirred tank. Intl J. Heat Mass Transfer 35 (8), 1957–1968.Google Scholar
Danckwerts, P. V. 1951 Significance of liquid-film coefficients in gas absorption. Ind. Engng Chem. 43 (6), 1460–1467.Google Scholar
Flores, O., Riley, J. J. & Horner-Devine, A. R. 2017 On the dynamics of turbulence near a free surface. J. Fluid Mech. 821, 248–265.Google Scholar
Fortescue, G. E. & Pearson, J. R. 1967 On gas absorption into a turbulent liquid. Chem. Engng Sci. 22 (9), 1163–1176.Google Scholar
Fredriksson, S. T., Arneborg, L., Nilsson, H., Zhang, Q. & Handler, R. A. 2016 An evaluation of gas transfer velocity parameterizations during natural convection using DNS. J. Geophys Res. 121 (2), 1400–1423.Google Scholar
Grötzbach, G. 1983 Spatial resolution requirements for direct numerical simulation of the Rayleigh–Bènard convection. J. Comput. Phys. 49, 241–264.Google Scholar
Handler, R. A., Saylor, J. R., Leighton, R. I. & Rovelstad, A. L. 1999 Transport of a passive scalar at a shear-free boundary in fully turbulent open channel flow. Phys. Fluids 11 (9), 2607–2625.Google Scholar
Hasegawa, Y. & Kasagi, N. 2008 Systematic analysis of high Schmidt number turbulent mass transfer across clean, contaminated and solid interfaces. Intl J. Heat Fluid Flow 29 (3), 765–773.Google Scholar
Herlina & Jirka, G. H. 2008 Experiments on gas transfer at the air–water interface induced by oscillating grid turbulence. J. Fluid Mech. 594, 183–208.Google Scholar
Herlina, H. & Wissink, J. G. 2014 Direct numerical simulation of turbulent scalar transport across a flat surface. J. Fluid Mech. 744, 217–249.Google Scholar
Herlina, H. & Wissink, J. G. 2016 Isotropic-turbulence-induced mass transfer across a severely contaminated water surface. J. Fluid Mech. 797, 665–682.Google Scholar
Hopfinger, E. J. & Toly, J.-A. 1976 Spatially decaying turbulence and its relation to mixing across density interfaces. J. Fluid Mech. 78 (1), 155–175.Google Scholar
Hunt, J. C. R. & Graham, J. M. R. 1978 Free-stream turbulence near plane boundaries. J. Fluid Mech. 84, 209–235.Google Scholar
Jähne, B. & Haussecker, H. 1998 Air–water gas exchange. Annu. Rev. Fluid Mech. 30, 443–468.Google Scholar
Janzen, J. G., Herlina, H., Jirka, G. H., Schulz, H. E. & Gulliver, J. S. 2010 Estimation of mass transfer velocity based on measured turbulence parameters. AIChE J. 56 (8), 2005–2017.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Jimenez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.Google Scholar
Khakpour, H. R., Shen, L. & Yue, D. K. P. 2011 Transport of passive scalar in turbulent shear flow under a clean or surfactant-contaminated free surface. J. Fluid Mech. 670, 527–557.Google Scholar
Kubrak, B., Herlina, H., Greve, F. & Wissink, J. G. 2013 Low-diffusivity scalar transport using a WENO scheme and dual meshing. J. Comput. Phys. 240, 158–173.Google Scholar
Lamont, J. C. & Scott, D. S. 1970 An eddy cell model of mass transfer into surface of a turbulent liquid. AIChE J. 16 (4), 513–519.Google Scholar
Ledwell, J. J. 1984 The variation of the gas transfer coefficient with molecular diffusity. In Gas Transfer at Water Surfaces, pp. 293–302. Springer.Google Scholar
Lewis, W. K. & Whitman, W. G. 1924 Principles of gas absorption. Ind. Engng Chem. 16 (12), 1215–1220.Google Scholar
Liu, X., Osher, S. & Chan, T. 1994 Weighted essentially non-oscillatory schemes. J. Comput. Phys. 115 (1), 200–212.Google Scholar
Magnaudet, J. 2003 High-Reynolds-number turbulence in a shear-free boundary layer: revisiting the Hunt–Graham theory. J. Fluid Mech. 484, 167–196.Google Scholar
Magnaudet, J. & Calmet, I. 2006 Turbulent mass transfer through a flat shear-free surface. J. Fluid Mech. 553, 155–185.Google Scholar
McCorquodale, M. W. & Munro, R. J. 2017 Experimental study of oscillating-grid turbulence interacting with a solid boundary. J. Fluid Mech. 813, 768–798.Google Scholar
McKenna, S. P. & McGillis, W. R. 2004 The role of free-surface turbulence and surfactants in air–water gas transfer. Intl J. Heat Mass Transfer 47 (3), 539–553.Google Scholar
Nagaosa, R. 1999 Direct numerical simulation of vortex structures and turbulent scalar transfer across a free surface in a fully developed turbulence. Phys. Fluids 11 (6), 1581–1595.Google Scholar
Nagaosa, R. & Handler, R. A. 2003 Statistical analysis of coherent vortices near a free surface in a fully developed turbulence. Phys. Fluids 15 (2), 375–394.Google Scholar
Pan, Y. & Banerjee, S. 1995 A numerical study of free–surface turbulence in channel flow. Phys. Fluids 7 (7), 1649–1664.Google Scholar
Perot, B. & Moin, P. 1995 Shear-free turbulent boundary layers. Part 1. Physical insights into near-wall turbulence. J. Fluid Mech. 295, 199–227.Google Scholar
Rodi, W. 2017 Turbulence modeling and simulation in hydraulics: a historical review. J. Hydraul. Engng 143 (5), 03117001.Google Scholar
Schwertfirm, F. & Manhart, M. 2007 DNS of passive scalar transport in turbulent channel flow at high Schmidt numbers. Intl J. Heat Fluid Flow 28 (6), 1204–1214.Google Scholar
Shen, L., Yue, D. K. P. & Triantafyllou, G. S. 2004 Effect of surfactants on free-surface turbulent flows. J. Fluid Mech. 506, 79–115.Google Scholar
Theofanous, T. G. 1984 Conceptual models of gas exchange. In Gas Transfer at Water Surfaces (ed. Brutsaert, W. & Jirka, G. H.), pp. 271–281. Springer.Google Scholar
Theofanous, T. G., Houze, R. N. & Brumfield, L. K. 1976 Turbulent mass transfer at free, gas liquid interfaces, with applications to open channel, bubble and jet flows. Intl J. Heat Mass Transfer 19 (6), 613–624.Google Scholar
Turney, D. E. & Banerjee, S. 2013 Air–water gas transfer and near-surface motions. J. Fluid Mech. 733, 588–624.Google Scholar
Variano, E. A. & Cowen, E. A. 2013 Turbulent transport of a high-Schmidt-number scalar near an air–water interface. J. Fluid Mech. 731, 259–287.Google Scholar
Walker, D. T., Leighton, R. I. & Garza-Rios, L. O. 1996 Shear-free turbulence near a flat free surface. J. Fluid Mech. 320, 19–51.Google Scholar
Wissink, J. G. 2004 On unconditional conservation of kinetic energy by finite-difference discretisations of the linear and non-linear convection equation. Comput. Fluids 33, 315–343.Google Scholar
Wissink, J. G., Herlina, H., Akar, Y. & Uhlmann, M. 2017 Effect of surface contamination on interfacial mass transfer rate. J. Fluid Mech. 830, 5–34.Google Scholar
Wissink, J. G. & Herlina, H. 2016 Direct numerical simulation of gas transfer across the air–water interface driven by buoyant convection. J. Fluid Mech. 787, 508–540.Google Scholar
Yang, D. & Shen, L. 2017 Direct numerical simulation of scalar transport in turbulent flows over progressive surface waves. J. Fluid Mech. 819, 58–103.Google Scholar