Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T16:32:23.227Z Has data issue: false hasContentIssue false
  • English
  • Français

Simulation and modelling of slip flow over surfaces grafted with polymer brushes and glycocalyx fibres

Published online by Cambridge University Press:  03 September 2012

Mingge Deng ,
Xuejin Li ,
Haojun Liang ,
Bruce Caswell  and
George Em Karniadakis
Mingge Deng
Affiliation:
Division of Applied Mathematics, Brown University, Providence, RI 02912, USA
Xuejin Li
Affiliation:
Division of Applied Mathematics, Brown University, Providence, RI 02912, USA
Haojun Liang
Affiliation:
CAS Key Laboratory of Soft Matter Chemistry, Department of Polymer Science and Engineering, and Hefei National Laboratory for Physical Sciences at Microscale, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Bruce Caswell
Affiliation:
School of Engineering, Brown University, Providence, RI 02912, USA
George Em Karniadakis*
Affiliation:
Division of Applied Mathematics, Brown University, Providence, RI 02912, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Fabrication of functionalized surfaces using polymer brushes is a relatively simple process and parallels the presence of glycocalyx filaments coating the luminal surface of our vasculature. In this paper, we perform atomistic-like simulations based on dissipative particle dynamics (DPD) to study both polymer brushes and glycocalyx filaments subject to shear flow, and we apply mean-field theory to extract useful scaling arguments on their response. For polymer brushes, a weak shear flow has no effect on the brush density profile or its height, while the slip length is independent of the shear rate and is of the order of the brush mesh size as a result of screening by hydrodynamic interactions. However, for strong shear flow, the polymer brush is penetrated deeper and is deformed, with a corresponding decrease of the brush height and an increase of the slip length. The transition from the weak to the strong shear regime can be described by a simple ‘blob’ argument, leading to the scaling 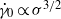, where 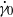is the critical transition shear rate and 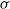is the grafting density. Furthermore, in the strong shear regime, we observe a cyclic dynamic motion of individual polymers, causing a reversal in the direction of surface flow. To study the glycocalyx layer, we first assume a homogeneous flow that ignores the discrete effects of blood cells, and we simulate microchannel flows at different flow rates. Surprisingly, we find that, at low Reynolds number, the slip length decreases with the mean flow velocity, unlike the behaviour of polymer brushes, for which the slip length remains constant under similar conditions. (The slip length and brush height are measured with respect to polymer mesh size and polymer contour length, respectively.) We also performed additional DPD simulations of blood flow in a tube with walls having a glycocalyx layer and with the deformable red blood cells modelled accurately at the spectrin level. In this case, a plasma cell-free layer is formed, with thickness more than three times the glycocalyx layer. We then find our scaling arguments based on the homogeneous flow assumption to be valid for this physiologically correct case as well. Taken together, our findings point to the opposing roles of conformational entropy and bending rigidity – dominant effects for the brush and glycocalyx, respectively – which, in turn, lead to different flow characteristics, despite the apparent similarity of the two systems.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Low-Reynolds-number flows: Low-Reynolds-number flows Non-Newtonian Flows: Non-Newtonian Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 711 , 25 November 2012 , pp. 192 - 211
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Adiga, S. P. & Brenner, D. W. 2005 Flow control through polymer-grafted smart nanofluidic channels: molecular dynamics simulations. Nano Lett. 5, 2509.CrossRefGoogle ScholarPubMed
2. Alexander, S. 1977 Adsorption of chain molecules with a polar head: a scaling description. J. Phys. (Paris) 38, 983.CrossRefGoogle Scholar
3. Anastassopoulos, D. L., Spiliopoulos, N., Vradis, A. A., Toprakcioglu, C., Baker, S. M. & Menelle, A. 2006 Shear-induced desorption in polymer brushes. Macromolecules 39, 8901.CrossRefGoogle Scholar
4. Aubouy, M., Harden, J. L. & Cates, M. E. 1996 Shear-induced deformation and desorption of grafted polymer layers. J. Phys. II 6, 969.Google Scholar
5. Baker, S. M., Smith, G. S., Anastassopoulos, D. L., Toprakcioglu, C., Vradis, A. A. & Bucknall, D. G. 2000 Structure of polymer brushes under shear flow in a good solvent. Macromolecules 33, 1120.CrossRefGoogle Scholar
6. Barrat, J. L. 1992 A possible mechanism for swelling of polymer brushes under shear. Macromolecules 25, 832.CrossRefGoogle Scholar
7. Birshtein, T. M., Borisov, O. V., Zhulina, E. B., Khokhlov, A. R. & Yurasova, T. A. 1987 Conformations of comb-like macromolecules. Polym. Sci. USSR 29, 1293.CrossRefGoogle Scholar
8. Brinkman, H. C. 1947 A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl. Sci. Res. A1, 27.Google Scholar
9. Broekhuizen, L. N., Mooij, H. L., Kastelein, J. J., Stroes, E. S., Vink, H. & Nieuwdorp, M. 2009 Endothelial glycocalyx as potential diagnostic and therapeutic target in cardiovascular disease. Curr. Opin. Lipidol. 20, 57–62.CrossRefGoogle ScholarPubMed
10. Damiano, E. R. 1998 The effect of the endothelial-cell glycocalyx on the motion of red blood cells through capillaries. Microvasc. Res. 55, 77–91.CrossRefGoogle ScholarPubMed
11. Damiano, E. R., Duling, B. R., Ley, K. & Skalak, T. C. 1996 Axisymmetric pressure-driven flow of rigid pellets through a cylindrical tube lined with a deformable porous wall layer. J. Fluid Mech. 314, 163–189.CrossRefGoogle Scholar
12. Damiano, E. R. & Stace, T. M. 2002 A mechano-electrochemical model of radial deformation of the capillary glycocalyx. Biophys. J. 82, 1153–1175.CrossRefGoogle ScholarPubMed
13. Deng, M., Jiang, Y., Liang, H. J. & Chen, Z. Y. J. 2010 Wormlike polymer brush: a self-consistent field treatment. Macromolecules 43, 3455.CrossRefGoogle Scholar
14. Doyle, P. S., Shaqfeh, E. S. G. & Gast, A. P. 1997 Rheology of ‘wet’ polymer brushes via Brownian dynamics simulation: steady vs oscillatory shear. Phys. Rev. Lett. 78, 1182.CrossRefGoogle Scholar
15. Espanol, P. & Warren, P. B. 1995 Statistical mechanics of dissipative particle dynamics. Europhys. Lett. 30, 191.Google Scholar
16. Fedosov, D. A., Caswell, B. & Karniadakis, G. E. 2010 A multiscale red blood cell model with accurate mechanics, rheology, and dynamics. Biophys. J. 98 (10), 2215–2225.CrossRefGoogle ScholarPubMed
17. Fedosov, D. A., Caswell, B., Suresh, S. & Karniadakis, G. E. 2011a Quantifying the biophysical characteristics of Plasmodium-falciparum-parasitized red blood cells in microcirculation. Proc. Natl Acad. Sci. USA 108, 35–39.CrossRefGoogle ScholarPubMed
18. Fedosov, D. A. & Karniadakis, G. E. 2009 Triple-decker: interfacing atomistic–mesoscopic–continuum flow regimes. J. Comput. Phys. 228, 1157.CrossRefGoogle Scholar
19. Fedosov, D. A., Pan, W., Caswell, B., Gompper, G. & Karniadakis, G. E. 2011b Predicting human blood viscosity in silico. Proc. Natl Acad. Sci. USA 108, 11772–11777.CrossRefGoogle ScholarPubMed
20. Gao, L. & Lipowsky, H. H. 2009 Measurement of solute transport in the endothelial glycocalyx using indicator dilution techniques. Ann. Biomed. Engng 37, 1781–1795.CrossRefGoogle ScholarPubMed
21. de Gennes, P. G. 1980 Conformations of polymers attached to an interface. Macromolecules 13, 1069.CrossRefGoogle Scholar
22. Grest, G. S. 1996 Interfacial sliding of polymer brushes: a molecular dynamics simulation. Phys. Rev. Lett. 76, 4979.CrossRefGoogle ScholarPubMed
23. Grest, G. S. 1999 Normal and shear forces between polymer brushes. Adv. Polym. Sci. 138, 149.CrossRefGoogle Scholar
24. Groot, R. D. & Warren, P. B. 1997 Dissipative particle dynamics: bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 107, 4423.Google Scholar
25. Guo, P., Weinstein, A. M. & Weinbaum, S. 2000 A hydrodynamic mechanosensory hypothesis for brush border microvilli. Am. J. Physiol. Renal Physiol. 279, F698–F712.Google Scholar
26. Han, Y., Weinbaum, S., Spaan, J. A. E. & Vink, H. 2006 Large-deformation analysis of the elastic recoil of fibre layers in a Brinkman medium with application to the endothelial glycocalyx. J. Fluid Mech. 554, 217–235.Google Scholar
27. Harden, J. L. & Cates, M. E. 1996 Deformation of grafted polymer layers in strong shear flows. Phys. Rev. E 53, 3782.CrossRefGoogle ScholarPubMed
28. Hoogerbrugge, P. J. & Koelman, J. M. V. A. 1992 Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys. Lett. 19, 155.Google Scholar
29. Huang, J., Wang, Y. & Laradji, M. 2006 Flow control by smart nanofluidic channels: a dissipative particle dynamics simulation. Macromolecules 39, 5546.CrossRefGoogle Scholar
30. Inn, Y. & Wang, S. Q. 1996 Hydrodynamic slip: polymer adsorption and desorption at melt/solid interfaces. Phys. Rev. Lett. 76, 467.CrossRefGoogle ScholarPubMed
31. Irfachsyad, D., Tildesley, D. & Malfreyt, P. 2002 Dissipative particle dynamics simulation of grafted polymer brushes under shear. Phys. Chem. Chem. Phys. 4, 3008.CrossRefGoogle Scholar
32. Ivkov, R., Bulter, P. D., Satija, S. K. & Fetters, L. J. 2001 Effect of solvent flow on a polymer brush: a neutron reflectivity study of the brush height and chain density profile. Langmuir 17, 2999.CrossRefGoogle Scholar
33. Kent, M. S., Lee, L. T., Factor, B. J., Rondelez, F. & Smith, G. S. 1995 Tethered chains in good solvent conditions: an experimental study involving Langmuir diblock copolymer monolayers. J. Chem. Phys. 103, 2320.CrossRefGoogle Scholar
34. Kim, Y., Lobaskin, Y., Gutsche, C., Kremer, F., Pincus, P. & Netz, R. 2009 Nolinear response of grafted semiflexible polymers in shear flow. Macromolecules 42, 3650–3655.Google Scholar
35. Klein, J., Kumacheva, E., Mahalu, D., Perahia, D. & Fetters, L. J. 1994 Reduction of frictional forces between solid surfaces bearing polymer brushes. Nature 370, 634.CrossRefGoogle Scholar
36. Klein, J., Perahia, D. & Warburg, S. 1991 Forces between polymer-bearing surfaces undergoing shear. Nature 352, 143.CrossRefGoogle Scholar
37. Kreer, T., Binder, K. & Muser, M. H. 2003 Friction between polymer brushes in good solvent conditions: steady-state sliding versus transient behaviour. Langmuir 19, 7551.CrossRefGoogle Scholar
38. Kumaran, V. 1993 Hydrodynamic interactions in flow past grafted polymers. Macromolecules 26, 2464.Google Scholar
39. Lai, P. Y. & Binder, K. 1993 Grafted polymer layers under shear: a Monte Carlo simulation. J. Chem. Phys. 98, 2366.CrossRefGoogle Scholar
40. Lei, H., Caswell, B. & Karniadakis, G. E. 2010 Direct construction of mesoscopic models from microscopic simulations. Phys. Rev. E 81, 026704.CrossRefGoogle ScholarPubMed
41. Miao, L., Guo, H. & Zuckermann, M. J. 1996 Conformation of polymer brushes under shear: chain tilting and stretching. Macromolecules 29, 2289.CrossRefGoogle Scholar
42. Milner, S. T. 1991a Hydrodynamic penetration into parabolic brushes. Macromolecules 24, 3704.CrossRefGoogle Scholar
43. Milner, S. T. 1991b Polymer brushes. Science 251, 905.CrossRefGoogle ScholarPubMed
44. Milner, S. T., Witten, T. A. & Cates, M. E. 1988 Theory of the grafted polymer brush. Macromolecules 21, 2610.CrossRefGoogle Scholar
45. Müller, M. & Pastorino, C. 2008 Cyclic motion and inversion of surface flow direction in a dense polymer brush under shear. Europhys. Lett. 81, 28002.Google Scholar
46. Nardai, M. M. & Zifferer, G. 2009 Simulation of dilute solutions of linear and star-branched polymers by dissipative particle dynamics. J. Chem. Phys. 131, 124903.Google Scholar
47. Netz, R. R. & Schick, M. 1998 Polymer brushes: from self-consistent field theory to classical theory. Macromolecules 31, 5105.CrossRefGoogle ScholarPubMed
48. Pastorino, C., Binder, K., Kreer, T. & Müller, M. 2006 Static and dynamic properties of the interface between a polymer brush and a melt of identical chains. J. Chem. Phys. 124, 064902.Google Scholar
49. Peters, G. H. & Tildesley, D. J. 1995 Computer simulation of the rheology of grafted chains under shear. Phys. Rev. E 52, 1882.CrossRefGoogle ScholarPubMed
50. Plimpton, S. 2011 LAMMPS: molecular dynamics simulator. http://lammps.sandia.gov.Google Scholar
51. Pries, A. R. & Secomb, T. W. 2005 Microvascular blood viscosity in vivo and the endothelial surface layer. Am. J. Physiol. Heart Circ. Physiol. 289, H2657–H2664.CrossRefGoogle ScholarPubMed
52. Pries, A. R., Secomb, T. W. & Gaehtgens, P. 2000 The endothelial surface layer. Pflugers Arch. 440, 653.Google Scholar
53. Pries, A. R., Secomb, T. W., Gessner, T., Sperandio, M. B., Gross, J. F. & Gaehtgens, P 1994 Resistance to blood flow in microvessels in vivo. Circulat. Res. 75, 904.Google Scholar
54. Rabin, Y. & Alexander, S. 1990 Stretching of grafted polymer layers. Europhys. Lett. 13, 49.CrossRefGoogle Scholar
55. Secomb, T. W., Hsu, R. & Pries, A. R. 1998 A model for red blood cell motion in glycocalyx-lined capillaries. Am. J. Physiol. Heart Circ. Physiol. 274, H1016–H1022.CrossRefGoogle Scholar
56. Secomb, T. W., Hsu, R. & Pries, A. R. 2001 Motion of red blood cells in a capillary with an endothelial surface layer: effect of flow velocity. Am. J. Physiol. Heart Circul. Physiol. 281, H629–H636.CrossRefGoogle Scholar
57. Sevick, E. M. & Williams, D. R. M. 1994 Polymer brushes as pressure-sensitive automated microvalves. Macromolecules 27, 5285.CrossRefGoogle Scholar
58. Squire, J. M., Chew, M., Nneji, G., Neal, C., Barry, J. & Michel, C. 2001 Quasi-periodic substructure in the microvessel endothelial glycocalyx: a possible explanation for molecular filtering? J. Struct. Biol. 136, 239–255.Google Scholar
59. Weinbaum, S., Tarbell, J. M. & Damiano, E. R. 2007 The structure and function of the endothelial glycocalyx layer. Annu. Rev. Biomed. Engng 9, 121–167.Google Scholar
60. Weinbaum, S., Zhang, X., Han, Y., Vink, H. & Cowin, S. C. 2003 Mechanotransduction and flow across the endothelial glycocalyx. Proc. Natl Acad. Sci. USA 100 (13), 7988–7995.Google Scholar
61. Wijmans, C. M. & Smit, B. 2002 Simulating tethered polymer layers in shear flow with the dissipative particle dynamics technique. Macromolecules 35, 7138.CrossRefGoogle Scholar
62. Zhulina, E. B., Borisov, O. V. & Pryamitsyn, V. A. 1990 Theory of steric stabilization of colloid dispersions by grafted polymers. J. Colloid Interface Sci. 137, 495.CrossRefGoogle Scholar
63. Zhulina, E. B. & Vilgis, T. A. 1995 Macromolecules 28, 1008.CrossRefGoogle Scholar