Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-24T19:42:49.011Z Has data issue: false hasContentIssue false
  • English
  • Français

A simple model for the reflection by a vertical barrier of a dambreak flow over a dry or pre-wetted bottom

Published online by Cambridge University Press:  20 May 2022

M. Ungarish Open the ORCID record for M. Ungarish [Opens in a new window]
M. Ungarish*
Affiliation:
Department of Computer Science, Technion, Haifa 32000, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

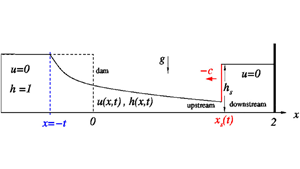
We revisit the theoretical solutions of the problem of the reflected flow from a vertical obstacle encountered by a current generated by dambreak of a Cartesian long reservoir over a dry bottom and with tailwaters. Previous investigations derived accurate solutions by quite complex manipulation of the balances along the characteristics, supported by numerical solutions, of the shallow-water equations (a significant extension is the recent paper Hogg & Skevington, Q. J. Mech. Appl. Maths, vol. 74, no. 4, 2021, pp. 441–465). Here we developed a simplified model, based on the major assumption that the fluid between the obstacle (wall) and the reflected jump is stagnant. This allows the solution of the problem by a straightforward numerical integration of one initial-value ordinary differential equation. The model provides the position, height and speed of the jump as functions of time. For long times a simple analytical approximation is also available. The model points out clear-cut effects of the presence of the tailwaters. The model has been validated by comparisons with exact solutions of the shallow-water equations of the recent study of Hogg & Skevington (Q. J. Mech. Appl. Maths, vol. 74, no. 4, 2021, pp. 441–465) (obtained by significantly more complex hodograph-plane methods). In all the tested cases the agreement is good, for long periods of time. This model provides reliable insights and fast quantitative predictions recommended for use in research and engineering problems where a fair approximation is sufficient for the application.

JFM classification

Geophysical and Geological Flows: Gravity currents
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 942 , 10 July 2022 , R6
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Baker, M., Ungarish, M. & Flynn, M. 2020 Tailwater gravity currents and their connection to perfectly subcritical flow: laboratory experiments and shallow-water and direct numerical solutions. Environ. Fluid Mech. 20 (4), 1141–1171.CrossRefGoogle Scholar
Greenspan, H.P. & Young, R.E. 1978 Flow over a containment dyke. J. Fluid Mech. 87, 179–192.CrossRefGoogle Scholar
Hogg, A.J. & Skevington, E.W.G. 2021 Dam-break reflection. Q. J. Mech. Appl. Maths 74 (4), 441–465.CrossRefGoogle Scholar
Ungarish, M. 2020 Gravity Currents and Intrusions — Analysis and Prediction. World Scientific.CrossRefGoogle Scholar