Article contents
Ship waves on uniform shear current at finite depth: wave resistance and critical velocity
Published online by Cambridge University Press: 24 February 2016
Abstract
We present a comprehensive theory for linear gravity-driven ship waves in the presence of a shear current with uniform vorticity, including the effects of finite water depth. The wave resistance in the presence of shear current is calculated for the first time, containing in general a non-zero lateral component. While formally apparently a straightforward extension of existing deep water theory, the introduction of finite water depth is physically non-trivial, since the surface waves are now affected by a subtle interplay of the effects of the current and the sea bed. This becomes particularly pronounced when considering the phenomenon of critical velocity, the velocity at which transversely propagating waves become unable to keep up with the moving source. The phenomenon is well known for shallow water, and was recently shown to exist also in deep water in the presence of a shear current (Ellingsen, J. Fluid Mech., vol. 742, 2014, R2). We derive the exact criterion for criticality as a function of an intrinsic shear Froude number 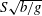 $S\sqrt{b/g}$ (
$S\sqrt{b/g}$ (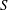 $S$ is uniform vorticity,
$S$ is uniform vorticity, 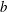 $b$ size of source), the water depth and the angle between the shear current and the ship’s motion. Formulae for both the normal and lateral wave resistance forces are derived, and we analyse their dependence on the source velocity (or Froude number
$b$ size of source), the water depth and the angle between the shear current and the ship’s motion. Formulae for both the normal and lateral wave resistance forces are derived, and we analyse their dependence on the source velocity (or Froude number 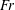 $Fr$) for different amounts of shear and different directions of motion. The effect of the shear current is to increase wave resistance for upstream ship motion and decrease it for downstream motion. Also the value of
$Fr$) for different amounts of shear and different directions of motion. The effect of the shear current is to increase wave resistance for upstream ship motion and decrease it for downstream motion. Also the value of 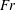 $Fr$ at which
$Fr$ at which 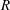 $R$ is maximal is lowered for upstream and increased for downstream directions of ship motion. For oblique angles between ship motion and current there is a lateral wave resistance component which can amount to 10–20 % of the normal wave resistance for side-on shear and
$R$ is maximal is lowered for upstream and increased for downstream directions of ship motion. For oblique angles between ship motion and current there is a lateral wave resistance component which can amount to 10–20 % of the normal wave resistance for side-on shear and 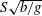 $S\sqrt{b/g}$ of order unity. The theory is fully laid out and far-field contributions are carefully separated off by means of Cauchy’s integral theorem, exposing potential pitfalls associated with a slightly different method (Sokhotsky–Plemelj) used in several previous works.
$S\sqrt{b/g}$ of order unity. The theory is fully laid out and far-field contributions are carefully separated off by means of Cauchy’s integral theorem, exposing potential pitfalls associated with a slightly different method (Sokhotsky–Plemelj) used in several previous works.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 38
- Cited by



