Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T16:09:05.232Z Has data issue: false hasContentIssue false
  • English
  • Français

Shear instability as a resonance between neutral waves hidden in a shear flow

Published online by Cambridge University Press:  09 January 2013

Keita Iga
Keita Iga*
Affiliation:
Atmosphere and Ocean Research Institute, The University of Tokyo, Kashiwa, Chiba 277-8564, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A concept which explains unstable modes by resonance between two neutral waves is applied to instability in shear flows with non-uniform potential vorticity distribution. In basic flows where shear instability occurs, a pair of neutral waves which should resonate to form an unstable mode does not exist mathematically unless the basic potential vorticity is uniform, owing to the shear of the basic flow. However, if a small window region is made where the potential vorticity of the basic flow is uniform, regular neutral modes can exist. The neutral wave located at the centre of this window region, which corresponds to a mode where the jump in its first derivative at one end of the window region cancels that at the other end, can be considered to be the hidden neutral wave. It is equivalent to a continuous mode which does not have a jump in its first derivative at the critical point even though it can have a singularity of 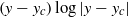$(y\ensuremath{-} {y}_{c} )\log \vert y\ensuremath{-} {y}_{c} \vert $, in the limit of an infinitely small window region. Thus, a method for retrieving neutral waves hidden in the shear of the basic flow is proposed here. By sweeping the basic flow range with this uniform potential vorticity window, all the features of the hidden neutral wave appear. By applying this method, shear instability in a flow with a tanh-shaped basic velocity profile is well explained via the resonance between neutral waves.

JFM classification

Waves/Free-surface Flows: Critical layers Wakes/Jets: Shear layers Waves/Free-surface Flows: Shear waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 715 , 25 January 2013 , pp. 452 - 476
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baines, P. G. & Mitsudera, H. 1994 On the mechanism of shear flow instabilities. J. Fluid Mech. 276, 327–342.Google Scholar
Bretherton, F. P. 1966 Critical layer instability in baroclinic flows. Q. J. Roy. Meteorol. Soc. 92, 325–334.CrossRefGoogle Scholar
Cairns, R. A. 1979 The role of negative energy waves in some instabilities of parallel flows. J. Fluid Mech. 92, 1–14.Google Scholar
Case, K. M. 1960 Stability of inviscid plane Couette flow. Phys. Fluids 3, 143–148.Google Scholar
Drazin, P. & Reid, W. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Gotoh, K. 1965 The damping of the large wavenumber disturbances in a free boundary layer flow. J. Phys. Soc. Japan 20, 164–169.Google Scholar
Hayashi, Y.-Y. & Young, W. R. 1987 Stable and unstable shear modes on rotating parallel flows in shallow water. J. Fluid Mech. 184, 477–504.Google Scholar
Iga, K. 1993 Reconsideration of Orlanski’s instability theory of frontal waves. J. Fluid Mech. 255, 213–236.CrossRefGoogle Scholar
Iga, K. 1997 Instability of a front with a layer of uniform potential vorticity. J. Met. Soc. Japan 75, 1–11.Google Scholar
Iga, K. 1999a Critical layer instability as a resonance between a non-singular mode and continuous modes. Fluid Dyn. Res. 25, 63–86.Google Scholar
Iga, K. 1999b A simple criterion for the sign of the pseudomomentum of modes in shallow water systems. J. Fluid Mech. 387, 343–352.CrossRefGoogle Scholar
Iga, K. & Ikazaki, H. 2000 Instability of a front formed by two layers with uniform potential vorticity. J. Met. Soc. Japan 78, 491–498.CrossRefGoogle Scholar
Lin, C. C. 1945 On the stability of two-dimensional parallel flows. Part 2. Q. Appl. Math. 3, 218–234.Google Scholar
Lin, C. C. 1961 Some mathematical problems in the theory of the stability of parallel flows. J. Fluid Mech. 10, 430–438.Google Scholar
Michalke, A. 1964 On the inviscid instability of the hyperbolic-tangent velocity profile. J. Fluid Mech. 19, 543–556.Google Scholar
Sakai, S. 1989 Rossby–Kelvin instability: a new type of ageostrophic instability caused by a resonance between Rossby waves and gravity waves. J. Fluid Mech. 202, 149–176.CrossRefGoogle Scholar
Taniguchi, H. & Ishiwatari, M. 2006 Physical interpretation of unstable modes of a linear shear flow in shallow water on an equatorial beta-plane. J. Fluid Mech. 567, 1–26.Google Scholar
Tatsumi, T, Gotoh, K. & Ayukawa, K. 1964 The stability of a free boundary layer at large Reynolds numbers. J. Phys. Soc. Japan 19, 1966–1980.Google Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.Google Scholar