Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-25T02:08:41.807Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-similarity of passive scalar flow in grid turbulence with a mean cross-stream gradient

Published online by Cambridge University Press:  03 September 2015

Carla Bahri ,
Gilad Arwatz ,
William K. George ,
Michael E. Mueller  and
Marcus Hultmark
Carla Bahri*
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Gilad Arwatz
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
William K. George
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Michael E. Mueller
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Marcus Hultmark
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Scaling of grid turbulence with a constant mean cross-stream temperature gradient is investigated using a combination of theoretical predictions and experimental data. A novel nanoscale temperature probe (T-NSTAP) was used to acquire temperature data. Conditions for self-similarity of the governing equations and the scalar spectrum are investigated, which reveals necessary conditions for the existence of a self-similar solution. These conditions provide a theoretical framework for scaling of the temperature spectrum as well as the temperature flux spectrum. One necessary condition, predicted by the theory, is that the characteristic length scale describing the scalar spectrum must vary as 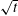$\sqrt{t}$ in the case of a zero virtual origin for a self-similar solution to exist. As predicted by the similarity analysis, the data show the variance growing as a power law with streamwise position. When scaled with the similarity variable, as found through the theoretical analysis, the temperature spectra show a good collapse over all wavenumbers. A new method to determine the quality of the scaling was developed, comparing the coefficient of variation. The minimum coefficient of variation, and thus the best scaling, for the measured spectra agrees well with the similarity requirements. The theoretical work also reveals an additional requirement related to the scaling of the scalar flux spectrum.

JFM classification

Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 780 , 10 October 2015 , pp. 215 - 225
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Department of Aeronautics, Imperial College London, South Kensington Campus, London SW7 2AZ, UK.

References

Antonia, R. A., Smalley, R. J., Zhou, T., Anselmet, F. & Danaila, L. 2004 Similarity solution of temperature structure functions in decaying homogeneous isotropic turbulence. Phys. Rev. E 69, 016305.Google Scholar
Arwatz, G., Bahri, C., Smits, A. J. & Hultmark, M. 2013 Dynamic calibration and modeling of a cold wire for temperature measurement. Meas. Sci. Technol. 24 (12), 125301.Google Scholar
Arwatz, G., Fan, Y., Bahri, C. & Hultmark, M. 2015 Development and characterization of a nano-scale temperature sensor (T-NSTAP) for turbulent temperature measurements. Meas. Sci. Technol. 26 (3), 035103.Google Scholar
Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 5, 113–133.Google Scholar
Benaissa, A., Djenidi, L., Antonia, R. A. & Parker, R. 2007 Effect of initial conditions on the scalar decay in grid turbulence at low $r{\it\lambda}$ . In Proceedings of the 16th Australasian Fluid Mechanics Conference, pp. 914–918. School of Engineering, The University of Queensland.Google Scholar
Comte-Bellot, G. & Corrsin, S. 1966 The use of a contraction to improve the isotropy of grid-generated turbulence. J. Fluid Mech. 25, 657–682.CrossRefGoogle Scholar
Comte-Bellot, G. & Corrsin, S. 1971 Simple Eulerian time correlation of full- and narrow-band velocity signals in grid-generated turbulence. J. Fluid Mech. 48, 273–337.CrossRefGoogle Scholar
Corrsin, S. 1952 Heat transfer in isotropic turbulence. J. Appl. Phys. 23 (1), 113–118.Google Scholar
Corrsin, S. 1964 Further generalization of Onsager’s cascade model for turbulent spectra. Phys. Fluids 7 (8), 1156–1159.Google Scholar
Donzis, D. A., Sreenivasan, K. R. & Yeung, P. K. 2005 Scalar dissipation rate and dissipative anomaly in isotropic turbulence. J. Fluid Mech. 532, 199–216.Google Scholar
Fossen, G. J. V. & Ching, C. Y. 1997 Measurements of the influence of integral length scale on stagnation region heat transfer. Intl J. Rotating Machinery 3 (2), 117–132.Google Scholar
George, W. K. & Gibson, M. M. 1992 The self-preservation of homogeneous shear flow turbulence. Exp. Fluids 13 (4), 229–238.CrossRefGoogle Scholar
George, W. K. 1992a The decay of homogeneous isotropic turbulence. Phys. Fluids A 4 (7), 1492–1509.Google Scholar
George, W. K. 1992b Self-preservation of temperature fluctuations in isotropic turbulence. In Studies in Turbulence (ed. Gatski, T. B., Speziale, C. G. & Sarkar, S.), pp. 514–528. Springer.CrossRefGoogle Scholar
Jayesh, T., Tong, C. N. & Warhaft, Z. 1994 On temperature spectra in grid turbulence. Phys. Fluids 6 (1), 306–312.Google Scholar
Monin, A. S., Yaglom, A. M. & Lumley, J. L. 1975 Statistical fluid mechanics: mechanics of turbulence. In Statistical Fluid Mechanics: Mechanics of Turbulence, vol. 2. MIT Press.Google Scholar
O’Neill, P., Nicolaides, D., Honnery, D. & Soria, J. 2004 Autocorrelation functions and the determination of integral length with reference to experimental and numerical data. In Proceedings of the 15th Australasian Fluid Mechanics Conference, The University of Sydney.Google Scholar
Overholt, M. R. & Pope, S. B. 1996 Direct numerical simulation of a passive scalar with imposed mean gradient in isotropic turbulence. Phys. Fluids 8 (11), 3128–3148.Google Scholar
Sinhuber, M., Bodenschatz, E. & Bewley, G. P. 2015 Decay of turbulence at high Reynolds numbers. Phys. Rev. Lett. 114, 034501.Google Scholar
Sirivat, A. & Warhaft, Z. 1983 The effect of a passive cross-stream temperature gradient on the evolution of temperature variance and heat flux in grid turbulence. J. Fluid Mech. 128, 323–346.Google Scholar
Speziale, C. G. & Bernard, P. S. 1992 The energy decay in self-preserving isotropic turbulence revisited. J. Fluid Mech. 241, 645–667.Google Scholar
Von Kármán, T. & Howarth, L. 1938 On the statistical theory of isotropic turbulence. Proc. R. Soc. Lond. A 164 (917), 192–215.Google Scholar
Wang, H. & George, W. K. 2002 The integral scale in homogeneous isotropic turbulence. J. Fluid Mech. 459, 429–443.Google Scholar
Warhaft, Z. 2000 Passive scalars in turbulent flows. Annu. Rev. Fluid Mech. 32 (1), 203–240.Google Scholar
Warhaft, Z. & Lumley, L. J. 1978 An experimental study of the decay of temperature fluctuations in grid-generated turbulence. J. Fluid Mech. 88, 659–684.Google Scholar
Yoon, K. & Warhaft, Z. 1990 The evolution of grid-generated turbulence under conditions of stable thermal stratification. J. Fluid Mech. 215, 601–638.Google Scholar