No CrossRef data available.
Article contents
Self-similar, spatially localized structures in turbulent pipe flow from a data-driven wavelet decomposition
Published online by Cambridge University Press: 13 September 2023
Abstract
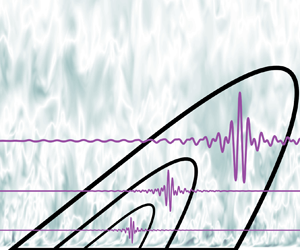
This study aims to extract and characterize structures in fully developed pipe flow at a friction Reynolds number of  $\textit {Re}_\tau = 12\,400$. To do so, we employ data-driven wavelet decomposition (DDWD) (Floryan & Graham, Proc. Natl Acad. Sci. USA, vol. 118, 2021, e2021299118), a method that combines features of proper orthogonal decomposition and wavelet analysis in order to extract energetic and spatially localized structures from data. We apply DDWD to streamwise velocity signals measured separately via a thermal anemometer at 40 wall-normal positions. The resulting localized velocity structures, which we interpret as being reflective of underlying eddies, are self-similar across streamwise extents of 40 wall units to one pipe radius, and across wall-normal positions from
$\textit {Re}_\tau = 12\,400$. To do so, we employ data-driven wavelet decomposition (DDWD) (Floryan & Graham, Proc. Natl Acad. Sci. USA, vol. 118, 2021, e2021299118), a method that combines features of proper orthogonal decomposition and wavelet analysis in order to extract energetic and spatially localized structures from data. We apply DDWD to streamwise velocity signals measured separately via a thermal anemometer at 40 wall-normal positions. The resulting localized velocity structures, which we interpret as being reflective of underlying eddies, are self-similar across streamwise extents of 40 wall units to one pipe radius, and across wall-normal positions from  $y^+=350$ to
$y^+=350$ to  $y/R=1$. Notably, the structures are similar in shape to Meyer wavelets. Projections of the data onto the DDWD wavelet subspaces are found to be self-similar as well, but in Fourier space; the bounds of self-similarity are the same as before, except streamwise self-similarity starts at a larger length scale of
$y/R=1$. Notably, the structures are similar in shape to Meyer wavelets. Projections of the data onto the DDWD wavelet subspaces are found to be self-similar as well, but in Fourier space; the bounds of self-similarity are the same as before, except streamwise self-similarity starts at a larger length scale of  $450$ wall units. The evidence of self-similarity provided in this study lends further support to Townsend's attached eddy hypothesis, although we note that the self-similar structures are detected beyond the log layer and extend to large length scales.
$450$ wall units. The evidence of self-similarity provided in this study lends further support to Townsend's attached eddy hypothesis, although we note that the self-similar structures are detected beyond the log layer and extend to large length scales.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press



