Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T14:27:51.180Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-similar invariant solution in the near-wall region of a turbulent boundary layer at asymptotically high Reynolds numbers

Published online by Cambridge University Press:  07 February 2020

Sajjad Azimi  and
Tobias M. Schneider Open the ORCID record for Tobias M. Schneider [Opens in a new window]
Sajjad Azimi
Affiliation:
Emergent Complexity in Physical Systems Laboratory (ECPS), École Polytechnique Fédérale de Lausanne, CH-1015Lausanne, Switzerland
Tobias M. Schneider*
Affiliation:
Emergent Complexity in Physical Systems Laboratory (ECPS), École Polytechnique Fédérale de Lausanne, CH-1015Lausanne, Switzerland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

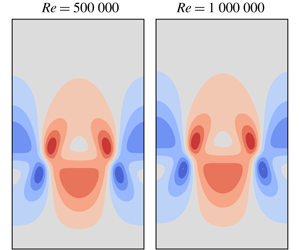
At sufficiently high Reynolds numbers, shear-flow turbulence close to a wall acquires universal properties. When length and velocity are rescaled by appropriate characteristic scales of the turbulent flow and thereby measured in inner units, the statistical properties of the flow become independent of the Reynolds number. We demonstrate the existence of a wall-attached non-chaotic exact invariant solution of the fully nonlinear three-dimensional Navier–Stokes equations for a parallel boundary layer that captures the characteristic self-similar scaling of near-wall turbulent structures. The branch of travelling wave solutions can be followed up to $Re=1\,000\,000$. Combined theoretical and numerical evidence suggests that the solution is asymptotically self-similar and exactly scales in inner units for Reynolds numbers tending to infinity. Demonstrating the existence of invariant solutions that capture the self-similar scaling properties of turbulence in the near-wall region is a step towards extending the dynamical systems approach to turbulence from the transitional regime to fully developed boundary layers.

JFM classification

Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 888 , 10 April 2020 , A15
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, M., Mellibovsky, F., Roland, N. & Hof, B. 2013 Streamwise-localized solutions at the onset of turbulence in pipe flow. Phys. Rev. Lett. 110 (22), 224502.CrossRefGoogle ScholarPubMed
Bobke, A., Örlü, R. & Schlatter, P. 2016 Simulations of turbulent asymptotic suction boundary layers. J. Turbul. 17 (2), 157–180.CrossRefGoogle Scholar
Chandler, G. J. & Kerswell, R. R. 2013 Invariant recurrent solutions embedded in a turbulent two-dimensional Kolmogorov flow. J. Fluid Mech. 722, 554–595.CrossRefGoogle Scholar
Cvitanović, P., Artuso, R., Mainieri, G., Tanner, G. & Vattay, G.2016 Chaos: Classical and Quantum. Niels Bohr Institute. Available at: chaosbook.org.Google Scholar
Deguchi, K. 2015 Self-sustained states at Kolmogorov microscale. J. Fluid Mech. 781, R6.CrossRefGoogle Scholar
Deguchi, K. & Hall, P. 2014a Free-stream coherent structures in parallel boundary-layer flows. J. Fluid Mech. 752, 602–625.CrossRefGoogle Scholar
Deguchi, K. & Hall, P. 2014b The high-Reynolds-number asymptotic development of nonlinear equilibrium states in plane Couette flow. J. Fluid Mech. 750, 99–112.CrossRefGoogle Scholar
Eckhardt, B. & Zammert, S. 2018 Small scale exact coherent structures at large Reynolds numbers in plane Couette flow. Nonlinearity 31 (2), R66–R77.CrossRefGoogle Scholar
Gibson, J. F., Halcrow, J. & Cvitanović, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.CrossRefGoogle Scholar
Gibson, J. F., Reetz, F., Azimi, S., Ferraro, A., Kreilos, T., Schrobsdorff, H., Farano, M., Yesil, A. F., Schütz, S. S., Culpo, M. et al. 2020 Channelflow 2.0. (in preparation). Available at: https://www.channelflow.ch.Google Scholar
Hocking, L. M. 1975 Non-linear instability of the asymptotic suction velocity profile. Q. J. Mech. Appl. Maths 28 (3), 341–353.CrossRefGoogle Scholar
Jiménez, J. 2018 Coherent structures in wall-bounded turbulence. J. Fluid Mech. 842, P1.CrossRefGoogle Scholar
Jiménez, J. & Simens, M. 2001 Low-dimensional dynamics of a turbulent wall flow. J. Fluid Mech. 435, 81–91.CrossRefGoogle Scholar
Kawahara, G., Uhlmann, M. & van Veen, L. 2012 The significance of simple invariant solutions in turbulent flows. Annu. Rev. Fluid Mech. 44 (1), 203–225.CrossRefGoogle Scholar
Khapko, T., Schlatter, P., Duguet, Y. & Henningson, D. S. 2016 Turbulence collapse in a suction boundary layer. J. Fluid Mech. 795, 356–379.CrossRefGoogle Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30 (04), 741–773.CrossRefGoogle Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.CrossRefGoogle Scholar
Neelavara, S. A., Duguet, Y. & Lusseyran, F. 2017 State space analysis of minimal channel flow. Fluid Dyn. Res. 49 (3), 035511.CrossRefGoogle Scholar
Park, J. S. & Graham, M. D. 2015 Exact coherent states and connections to turbulent dynamics in minimal channel flow. J. Fluid Mech. 782, 430–454.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Rawat, S., Cossu, C., Hwang, Y. & Rincon, F. 2015 On the self-sustained nature of large-scale motions in turbulent Couette flow. J. Fluid Mech. 782, 515–540.CrossRefGoogle Scholar
Rawat, S., Cossu, C. & Rincon, F. 2016 Travelling-wave solutions bifurcating from relative periodic orbits in plane Poiseuille flow. C. R. Méc 344 (6), 448–455.CrossRefGoogle Scholar
Reetz, F., Kreilos, T. & Schneider, T. M. 2019 Exact invariant solution reveals the origin of self-organized oblique turbulent-laminar stripes. Nature Commun. 10 (1), 2277.CrossRefGoogle ScholarPubMed
Schlatter, P. & Örlü, R. 2011 Turbulent asymptotic suction boundary layers studied by simulation. J. Phys.: Conf. Ser. 318 (2), 022020.Google Scholar
Schlichting, H. 2004 Boundary-layer Theory. Springer.Google Scholar
Schneider, T. M., Eckhardt, B. & Yorke, J. A. 2007 Turbulence transition and the edge of chaos in pipe flow. Phys. Rev. Lett. 99, 34502.CrossRefGoogle ScholarPubMed
Skufca, J. D., Yorke, J. A. & Eckhardt, B. 2006 Edge of chaos in a parallel shear flow. Phys. Rev. Lett. 96, 174101.CrossRefGoogle Scholar
Suri, B., Tithof, J., Grigoriev, R. O. & Schatz, M. F. 2017 Forecasting fluid flows using the geometry of turbulence. Phys. Rev. Lett. 118 (11), 114501.CrossRefGoogle ScholarPubMed
Wang, J., Gibson, J. F. & Waleffe, F. 2007 Lower branch coherent states in shear flows: transition and control. Phys. Rev. Lett. 98 (20), 204501.CrossRefGoogle ScholarPubMed
Yang, Q., Willis, A. P. & Hwang, Y. 2019 Exact coherent states of attached eddies in channel flow. J. Fluid Mech. 862, 1029–1059.CrossRefGoogle Scholar