Self-radiation force on a moving monopolar source

Abstract

The radiation force exerted on an object by an acoustic wave is a widely studied phenomenon since the early work of Rayleigh, Langevin and Brillouin, and has led in the last decade to tremendous developments for acoustic micromanipulation. Despite extensive work on this phenomenon, the expressions of the acoustic radiation force applied on a particle have so far been derived only for a steady particle, hence neglecting the effect of its displacement on the radiated wave. In this work, we study the acoustic radiation force exerted on a monopolar source translating at a constant velocity that is small compared to the sound speed. We demonstrate that the asymmetry of the emitted field resulting from the Doppler effect induces a radiation force on the source opposite to its motion.

1. Introduction

Since the seminal work by Rayleigh (1902, 1905) and Langevin (work reported later by Biquard 1932a,b), much effort has been devoted to the derivation of theoretical expressions of the acoustic radiation force exerted by an acoustic wave on a particle. Brillouin (1925a,b) was the first to recognize the tensorial nature of the acoustic radiation force, which is not necessarily orthogonal to the insonified interface. Later on, King (1934) derived an expression of the axial acoustic radiation force exerted on a rigid spherical particle by a plane wave. This expression was extended to the cases of a compressible fluid sphere and an elastic particle by Yosika & Kawasima (1955) and Hasegawa & Yosika (1969), respectively. The case of an incident focused wave was treated by Embleton (1954) for a rigid particle, and by Chen & Apfel (1996) for an elastic particle. Later on, the more general case of the axial force exerted by a Bessel beam was addressed by Marston (2006, 2009).

In parallel, a general expression of the acoustic radiation force exerted by an arbitrary wavefield on a spherical particle in the long wavelength regime (LWR; i.e. when $ka \ll 1$, with $k$ the wavenumber, and $a$ the particle radius) was obtained by Gork'ov (1962). It was shown up to third order (in $ka$) that the radiation force is proportional to the gradient of an acoustic potential, which is proportional to the difference between the time-averaged potential and kinetic acoustic energy weighed respectively by the monopole and dipole scattering coefficients. This expression was extended to sixth order by Sapozhnikov & Bailey (2013), which is necessary when the average potential and kinetic energy are uniform in space (e.g. for plane propagating waves). This expression was also extended by Doinikov (1997a,b,c) to consider the effect of the viscous and thermal boundary layers in some asymptotic limits (of the boundary layer size compared to the particle size), and in the general case by Settnes & Bruus (2012) and Karlsen & Bruus (2015). The cases of non-spherical particles such as disks and spheroids were treated by Keller (1957) and Silva & Drinkwater (2018), respectively, while the case of transient acoustic fields was recently addressed by Wang et al. (2021). We can also note that some expressions for the secondary radiation force (inter-particle force) have been derived by Silva & Bruus (2011). The specific case of the radiation force exerted on a vibrating bubble known as the primary Bjerknes force was treated separately by Bjerknes (1906), Blake (1949), Eller (1968) and Crum (1975). Indeed, bubbles have some specificity: owing to their strong compressibility compared to the surrounding liquid, their monopolar resonance appears in the LWR. Hence bubbles can be attracted to the nodes or anti-nodes of a standing wave depending on whether they are forced below or above their monopolar resonance frequency (see Eller 1968).

Recently, there has been some renewed interest in the calculation of the acoustic radiation force with the development of selective acoustical tweezers (see Baudoin & Thomas (2020) for a review of the subject). Acoustical tweezers rely on the acoustic radiation force to move objects. To reach selectivity, i.e. the ability to manipulate a single object independently of other neighbouring objects, it is necessary to localize the acoustic energy close to the target particle to affect it alone (see e.g. Baresch, Thomas & Marchiano 2016; Baudoin et al. 2019, 2020). Hence such selectivity cannot be reached in the LWR. In addition, to calculate the restoring force (i.e. the force that brings back the particle towards the trap centre), it is necessary to compute the radiation force when the particle is out-centred from the trap position. Yet all the aforementioned expressions were limited either to the calculation of the radiation force for an axisymmetric configuration or to the LWR. To cope with this issue, general expressions of the radiation force exerted by an arbitrary incident field on a spherical particle, without restriction on the particle size compared to the wavelength, were obtained by Sapozhnikov & Bailey (2013) with an angular-spectrum-based method, and by Silva (2011) and Baresch, Thomas & Marchiano (2013) with a multipole expansion method. The equivalence between the formulas obtained with the different approaches was demonstrated by Gong & Baudoin (2021). Note also that some general expressions have been proposed to compute the acoustic radiation torque exerted by an arbitrary acoustic field on a particle of arbitrary size by Silva, Lobo & Mitri (2012) and Gong & Baudoin (2020).

Yet in all the theoretical developments mentioned so far, the calculation of the radiation force is made for a steady particle, hence neglecting the effect of its motion. Some account of the interaction between the oscillatory and translational motion of bubbles can be found in the literature. First, erratic motion of bubbles resulting from complex coupling between oscillatory and translational motion was reported by Gaines (1932), Kornfeld & Suvorov (1944), Strasberg & Benjamin (1958), Eller & Crum (1970), and many others since. It was first suggested by Benjamin & Strasberg (1958), and demonstrated quantitatively by Eller & Crum (1970), that this erratic motion is related to some parametrically excited shape oscillations of the bubble. In an attempt to rationalize this behaviour, and following Saffman (1967), Benjamin & Ellis (1990) showed that even in an inviscid fluid, self-propulsion of a bubble can be achieved by nonlinear interactions between adjacent surface deformation modes. In their work, however, the surface mode deformations are supposed to be known a priori. This work was extended later by Mei & Zhou (1991) to account for the parametric excitation of surface modes by the isotropic volume mode, and by Feng & Leal (1995), who considered the direct coupling between translational motion, volume and shape modes. Finally, Doinikov (2004) obtained an expression of this coupling whatever the shape modes, their natural frequency, and the type of excitation (parametric forcing by the volume mode or direct excitation through externally induced pressure gradients at the surface of the bubble). In parallel, it was also shown by Watanabe & Kukita (1993) and Doinikov (2002) that even if the bubble oscillations remain spherical, some complex coupling between volumetric oscillations and translational motion leading to erratic motion of the bubble can still occur when the bubble is excited by acoustic standing waves of high intensity. Finally, we can mention the work of Magnaudet & Legendre (1998), who computed how the viscous drag applied on a translating bubble is modified by its oscillation.

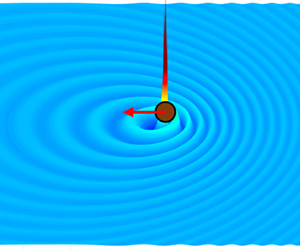
But none of these works considered the effect of the asymmetry of the acoustic wave radiated by a translating source on the acoustic radiation force. In this paper, we consider a monopolar source translating in a quiescent inviscid fluid at constant velocity $U$ along a fixed axis, and demonstrate that the asymmetry of the acoustic field due to the Doppler effect (figure 1) induces a self-induced radiation force on the source resisting its motion. This result is obtained by inserting the well-known solution of the wavefield radiated by a moving monopolar source into a far-field integral expression of the radiation force exerted on a moving source, and finally computing this integral within the approximation of slow translating speed compared to the sound speed.

Figure 1. Sketch illustrating the asymmetry of the acoustic field synthesized by a translating monopolar source. The normalized field is calculated with (2.21), and for the sake of illustration, the asymmetry is magnified by choosing Mach number $M = 0.5$.

2. Wavefield radiated by a translating monopolar source

The first step to compute the self-induced radiation force exerted on a moving monopolar source is to compute the wavefield radiated by this source in a fixed reference frame. This classic calculation can be found in the acoustics textbook of Morse & Ingard (1968). In this section, we recall the main steps of the derivation. Here, we suppose the fluid to be inviscid.

2.1. Wave equation for a translating monopolar source

In acoustics, a monopolar source can be seen as a source of mass, whose strength is specified by the instantaneous mass flow rate $q(t)$ created by this source. In the following, the source is supposed to be periodic of period $T$. For a punctual source translating at velocity $\boldsymbol {U} = U \boldsymbol {x} = M c_o \, \boldsymbol {x}$ along a fixed axis $\boldsymbol {x}$, the mass and momentum conservation equations become

(2.1)$$\begin{gather} \frac{\partial\rho}{\partial t}+{\boldsymbol{\nabla}}\boldsymbol{\cdot}(\rho\boldsymbol{v})= q(t)\,\delta(x-M c_0 t)\,\delta(y)\,\delta(z), \end{gather}$$

(2.2)$$\begin{gather}\frac{\partial\rho\boldsymbol{v}}{\partial t} +{\boldsymbol{\nabla}}\boldsymbol{\cdot}(\rho\boldsymbol{v}\otimes\boldsymbol{v})= \boldsymbol{\nabla}\boldsymbol{\cdot}\bar{\bar{\sigma}} , \end{gather}$$

with $\mathcal {R} = (O,(x,y,z),t)$ a Galilean reference frame, $M$ the Mach number, $c_o$ the sound speed, $\rho$ the density, $\boldsymbol {v}$ the fluid velocity, $\bar {\bar {\sigma }}$ the stress tensor equal to $-p \bar {\bar {I}}$ for an inviscid fluid, $\bar {\bar {I}}$ the identity tensor, and $p$ the pressure. If we (i) make the classic asymptotic development of (2.1) and (2.2) up to first order,

(2.3a, 2.3b and 2.3c) \begin{cases}{} \rho = \rho_0 + \epsilon \rho_1,\\ p = p_0 + \epsilon p_1,\\ \boldsymbol{v} = \boldsymbol{v}_0 + \epsilon \boldsymbol{v}_1, \end{cases}

with $\epsilon \ll 1$, and obtain the linearized mass and momentum balance

(2.4)$$\begin{gather} \frac{\partial\rho_1}{\partial t}+\rho_0\,\boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{v}_1=q(t)\,\delta(x-M c_0 t)\, \delta(y)\,\delta(z), \end{gather}$$

(2.5)$$\begin{gather}\rho_0\,\frac{\partial\boldsymbol{v}_1}{\partial t}={-}\boldsymbol{\nabla} p_1, \end{gather}$$

(ii) introduce the sound speed

(2.6)\begin{equation} c_0^2 = \left(\frac{\partial p}{\partial\rho}\right)_s = \frac{p_1}{\rho_1}, \end{equation}

where $s$ is the entropy, and (iii) combine the time derivative of (2.4) with the divergence of (2.5), then we obtain the wave equation

(2.7)\begin{equation} \varDelta p_1 -\frac{1}{c_0^2}\,\frac{\partial^2p_1}{\partial t^2}={-}\frac{\partial}{\partial t} \left[ q(t)\,\delta(x-M c_0 t)\,\delta(y)\,\delta(z) \right]. \end{equation}

Note that to ease the resolution of this problem, it is convenient to introduce the velocity potential $\psi _1$ defined by $\boldsymbol {v}_1=-({1}/{\rho _0})\,\boldsymbol {\nabla }\psi _1$ such that $p_1={\partial \psi _1}/{\partial t}$, which enables us to suppress the time derivative in the right-hand side of (2.7),

(2.8)\begin{equation} \varDelta\psi_1 -\frac{1}{c_0^2}\,\frac{\partial^2\psi_1}{\partial t^2}={-}q(t)\,\delta(x-M c_0 t)\,\delta(y)\,\delta(z), \end{equation}

and will make the future change of variables easier.

2.2. Resolution of the wave equation and Lorentz transformation

The solution of the wave equation (2.8) is well-known for a fixed monopolar source ($M=0$):

(2.9)\begin{equation} \psi_1(r,t)= \frac{q(t\pm r/c_0 )}{4{\rm \pi} r}, \end{equation}

with $r = \sqrt {x^2 + y^2 + z^2}$ the radial distance. To solve the problem for the moving source, the idea is to rewrite (2.8) in a reference frame wherein the source is fixed and the wave equation remains unchanged. This can be achieved by using the invariance of the wave equation by the Lorentz transformation, which is at the core of special relativity:

(2.10a, 2.10b, 2.10c and 2.10d) \begin{cases}{} x'=\gamma(x -M c_0 t),\\ y'=y,\\ z'=z,\\ c_0 t'=\gamma(c_0 t -M x),\end{cases}

where $\gamma$, defined by $\gamma ^{-1}=\sqrt {1-M ^2}$, is the ‘Lorentz acoustic boost’. With this transformation, the wave equation (2.8) becomes

(2.11)\begin{equation} \varDelta'\psi_1 -\frac{1}{c_0^2}\,\frac{\partial^2 \psi_1}{\partial t'^2}={-}q\left(\gamma(t'+M x'/c)\right)\delta(x'/\gamma)\,\delta(y')\,\delta(z'). \end{equation}

Since the right-hand side of (2.11) is null when $x'\neq 0$ for all $t'$, and using $\delta (x'/\gamma )=\gamma \,\delta (x')$, we obtain

(2.12)\begin{equation} \varDelta' \psi_1 -\frac{1}{c_0 ^2}\,\frac{\partial^2 \psi_1}{\partial t'^2}={-}\gamma\,q(\gamma t')\,\delta(x')\,\delta(y')\,\delta(z'). \end{equation}

If we now introduce a second set of variables,

(2.13a, 2.13b, 2.13c and 2.13d) \begin{cases}{} x''=\gamma x',\\ y''=\gamma y',\\ z''=\gamma z',\\ c_0 t''=\gamma c_0 t', \end{cases}

then the wave equation becomes

(2.14)\begin{equation} \varDelta'' \psi_1 -\frac{1}{c_0 ^2}\,\frac{\partial^2 \psi_1}{\partial t''^2}={-}\gamma^2\,q(t'')\,\delta(x'')\,\delta(y'')\,\delta(z''), \end{equation}

which now resembles the static monopolar source problem, and whose solution is

(2.15)\begin{equation} \psi_1(r'',t'')= \gamma^2\,\frac{q(t''\pm r''/c_0 )}{4{\rm \pi} r''}. \end{equation}

If we now perform the inverse transformations to obtain the potential as a function of $(x,y,z,t)$, then we obtain

(2.16)\begin{equation} \psi_1(r',t')= \gamma^2\,\frac{q(\gamma(t'\pm r'/c_0 ))}{4{\rm \pi}\gamma r'}, \end{equation}

with

(2.17)\begin{align} \gamma\left(t'\pm \frac{r'}{c_0}\right) & = \frac{\gamma}{c_0}\left[\gamma(c_0 t-M x) \pm \sqrt{[\gamma(x-M c_0 t)]^2+y^2+z^2}\right] \end{align}

(2.18)\begin{align} & = t -\frac{M (x-M c_0 t)\pm\sqrt{(x-M c_0 t)^2+(y^2+z^2)(1-M ^2)}}{c_0 (1-M ^2)}. \end{align}

We can now introduce the distance $R_\pm$ between the emission and observation points:

(2.19)\begin{equation} R_\pm=\frac{M(x-M c_0 t)\pm R_1}{1-M^2}, \end{equation}

with

(2.20)\begin{equation} R_1=\sqrt{(x-M c_0 t)^2+(y^2+z^2)(1-M^2)}. \end{equation}

As $R_\pm$ is a distance (positive by definition), $R = R_+$ when the Mach number is $M<1$, and $R=R_-$ for Mach numbers $M>1$. Here, we consider only small Mach numbers so that $R_\pm = R_+$. For an outgoing wave radiated by the source, the solution becomes

(2.21)\begin{equation} \boxed{ \psi_1(r,t)=\frac{q(t-R/c_0 )}{4{\rm \pi} R_1}. } \end{equation}

3. Integral expression of the radiation stress in the far field

The next step is to derive a far-field integral expression of the radiation stress exerted on a moving source. Indeed, in acoustics, a monopolar point source constitutes a far-field approximation of a real source of finite extent, hence the above expressions are valid only in the far field.

3.1. Far-field expression of the radiation force for a moving source

The acoustic radiation stress exerted on an object of surface $\mathcal {S}(t)$ is by definition the time average of the surface integral of the stress exerted by the acoustic wave on its surface:

(3.1)\begin{equation} \left\langle\boldsymbol{F}_{{rad}}\right\rangle=\left\langle\iint_{\mathcal{S}(t)}\bar{\bar{\sigma}}\boldsymbol{n} \,{\rm d}S\right\rangle, \end{equation}

where $\left \langle \,f \right \rangle = ({1}/{T}) \int _t^{t+T} f(t) \,{\rm d}t$ is the time average of the function $f$, and $T$ is the period of the function $f(t)$. In general, there are two difficulties when computing this integral: (i) the surface of the object is vibrating and hence depends on time ($\mathcal {S} = \mathcal {S}(t)$); and (ii) an expression for the wave scattered by the object in the near field must be known. Hence generally, this integral is converted into an integral over a closed surface at rest surrounding the object in the far field by using the divergence theorem and Reynolds transport theorem (see e.g. the review by Baudoin & Thomas (2020) for details of this process). Here, an additional difficulty comes from the fact that the particle, in addition to its vibration, is translating at a constant velocity $U$. To solve this issue, we will transpose our integral of the stress on the surface of the object into an integral over a spherical surface $\mathcal {S}_{\infty }$ of radius $r_{\infty } \gg \lambda$, centred on the source, and hence translating at velocity $\boldsymbol {U}$ in $\mathcal {R}$ (see figure 2), with $\lambda = c_0 / f$ the wavelength, and $f$ the frequency. The volume between $\mathcal {S}$ and $\mathcal {S}_{\infty }$ is named $\mathcal {V}$. The integral of (2.2) over $\mathcal {V}$ gives

(3.2)\begin{equation} \iiint_\mathcal{V}{\left[\frac{\partial\rho\boldsymbol{v}}{\partial t} +\boldsymbol{\nabla}\boldsymbol{\cdot}\left(\rho\boldsymbol{v}\otimes\boldsymbol{v} -\bar{\bar{\sigma}}\right)\right] {\rm d}V}= \boldsymbol{0}. \end{equation}

Using the divergence theorem, this volume integral turns into

(3.3)\begin{equation} \iiint_\mathcal{V}{\frac{\partial\rho\boldsymbol{v}}{\partial t}\,{\rm d}V} -\iint_\mathcal{S}\left(\rho\boldsymbol{v}\otimes\boldsymbol{v}-\bar{\bar{\sigma}}\right)\boldsymbol{n} \,{\rm d}S +\iint_{\mathcal{S}_{\infty}} \left( \rho \boldsymbol{v} \otimes \boldsymbol{v} - \bar{\bar{\sigma}} \right) \boldsymbol{n}_\infty \,{\rm d}S= \boldsymbol{0}, \end{equation}

with $\boldsymbol {n}$ and $\boldsymbol {n}_\infty$ the outgoing normal vectors to the surfaces $\mathcal {S}$ and $\mathcal {S}_{\infty }$, respectively (see figure 2). Another equation can be obtained by applying the Reynolds transport theorem to the momentum density $\rho \boldsymbol {v}$, i.e.

(3.4)\begin{equation} \frac{{\rm d}}{{\rm d}t}\iiint_{\mathcal{V}}\rho\boldsymbol{v} \,{\rm d}V= \iiint_{\mathcal{V}}\frac{\partial \rho\boldsymbol{v}}{\partial t}\,{\rm d}V -\iint_\mathcal{S}(\boldsymbol{v}\boldsymbol{\cdot}\boldsymbol{n})\rho\boldsymbol{v} \,{\rm d}S +\iint_{\mathcal{S}_{\infty}}(\boldsymbol{U }\boldsymbol{\cdot}\boldsymbol{n}_\infty)\rho\boldsymbol{v} \,{\rm d}S, \end{equation}

since the surface $\mathcal {S}$ follows the object surface displacement (equal to the fluid displacement at the interface due to the continuity condition), and the surface $\mathcal {S}_{\infty }$ is translating at a constant velocity $\boldsymbol {v}$. If we study the steady regime, then

(3.5)\begin{equation} \left\langle\frac{{\rm d}}{{\rm d}t}\iiint_{\mathcal{V}}\rho\boldsymbol{v} \,{\rm d}V\right\rangle=\boldsymbol{0}. \end{equation}

Finally, if we subtract the time average of (3.4) from the time average of (3.3), and take into account (3.5), then we obtain

(3.6)\begin{equation} \left\langle\boldsymbol{F}_{{rad}}\right\rangle=\left\langle\iint_{\mathcal{S}_{\infty}} \left(\bar{\bar{\sigma}}-\rho\boldsymbol{v}\otimes\boldsymbol{v}\right)\boldsymbol{n}_\infty \,{\rm d}S\right\rangle +\left\langle\iint_{\mathcal{S}_{\infty}} (\boldsymbol{U }\boldsymbol{\cdot}\boldsymbol{n}_\infty)\rho\boldsymbol{v} \,{\rm d}S\right\rangle. \end{equation}

Figure 2. Here, $\mathcal {S}$ represents the source surface, varying over time. The surface $\mathcal {S}_{\infty }$ is centred on the source and moves with it at velocity $\boldsymbol {U }$ in $\mathcal {R}$. The frame of the source is denoted $\mathcal {R}^*$.

3.2. Expression as a function of the first-order acoustic field

In order to compute the previous integrals, and since the time average of first-order terms is equal to $\boldsymbol {0}$ for a periodic signal, we need to express the terms appearing in (3.6) up to second order. Here, we suppose again that the fluid is inviscid and hence $\bar {\bar {\sigma }} = - p \bar {\bar {I}}$. If we push the asymptotic development up to second order, i.e.

(3.7a, 3.7b and 3.7c) \begin{cases}{} \rho=\rho_0+\epsilon \rho_1+ \epsilon^2 \rho_2,\\ p=p_0+\epsilon p_1+ \epsilon^2 p_2,\\ \boldsymbol{v}= \epsilon \boldsymbol{v}_1+ \epsilon^2 \boldsymbol{v}_2, \end{cases}

then the momentum balance (2.2) at second order in the volume $\mathcal {V}$ becomes

(3.8)\begin{equation} \rho_0\,\frac{\partial\boldsymbol{v}_2}{\partial t} +\rho_1\,\frac{\partial\boldsymbol{v}_1}{\partial t} +\rho_0 \left( \boldsymbol{v}_1\,\boldsymbol{\nabla} \boldsymbol{v}_1 \right) ={-}\boldsymbol{\nabla} p_2. \end{equation}

If we take the time average of this equation, then we obtain

(3.9)\begin{equation} \left\langle-\boldsymbol{\nabla} p_2\right\rangle=\left\langle\rho_1\,\frac{\partial \boldsymbol{v}_1}{\partial t}+\rho_0\left( \boldsymbol{v}_1\,\boldsymbol{\nabla} \boldsymbol{v}_1 \right) \right\rangle, \end{equation}

since $\left \langle {\partial \boldsymbol {v}_2}/{\partial t}\right \rangle =\boldsymbol {0}$ in the steady regime. From the first-order momentum conservation equation (2.5), we have ${\partial \boldsymbol {v}_1}/{\partial t} = - ({1}/{\rho _0} )\,\boldsymbol {\nabla } p_1$, and from the state equation (2.6), we have $\rho _1 = p_1 / c_0^2$, leading to

(3.10)\begin{equation} \rho_1\,\frac{\partial \boldsymbol{v}_1}{\partial t} ={-}\frac{1}{2\rho_0c_0 ^2}\,\boldsymbol{\nabla} p_1^2. \end{equation}

And since the acoustic field is by definition irrotational, we have

(3.11)\begin{equation} \rho_0\left( \boldsymbol{v}_1\,\boldsymbol{\nabla} \boldsymbol{v}_1 \right) = \frac{\rho_0}{2}\,\boldsymbol{\nabla}\boldsymbol{v}_1^2. \end{equation}

Finally, by replacing (3.10) and (3.11) in (3.9), we obtain

(3.12)\begin{equation} \left\langle-\boldsymbol{\nabla} p_2\right\rangle= \left\langle-\frac{1}{2\rho_0c_0 ^2}\,\boldsymbol{\nabla} p_1^2 +\frac{\rho_0}{2}\,\boldsymbol{\nabla}\boldsymbol{v}_1^2\right\rangle. \end{equation}

From this equation, we obtain the second-order averaged stress tensor:

(3.13)\begin{equation} \left\langle \bar{\bar{\sigma}}_2 \right\rangle={-}\left\langle p_2 \bar{\bar{I}} \right\rangle = \left\langle \left(\rho_0\,\frac{v_1^2}{2} -\frac{1}{\rho_0c_0^2}\,\frac{p_1^2}{2}\right)\bar{\bar{I}} \right\rangle. \end{equation}

Then at second order, we have

(3.14)$$\begin{gather} \left\langle \rho\boldsymbol{v}\otimes\boldsymbol{v} \right\rangle = \left\langle \rho_0 \boldsymbol{v}_1 \otimes\boldsymbol{v}_1 \right\rangle, \end{gather}$$

(3.15)$$\begin{gather}\left\langle \rho \boldsymbol{v} \right\rangle = \left\langle \rho_1 \boldsymbol{v}_1 \right\rangle , \end{gather}$$

so that if we replace (3.13), (3.14) and (3.15) in (3.6), we obtain the final expression of the radiation force as a function of the first-order acoustic fields:

(3.16)\begin{align} \boxed{ \left\langle\boldsymbol{F}_{{rad}}\right\rangle= \left\langle\iint_{\mathcal{S}_{\infty}}{\left[\left(\rho_0\,\frac{v_1^2}{2}-\frac{1}{\rho_0c_0^2}\,\frac{p_1^2}{2}\right) \bar{\bar{I}} -\rho_0\boldsymbol{v}_1\otimes\boldsymbol{v}_1 \right]}\boldsymbol{n} \,{\rm d}S\right\rangle +\left\langle\iint_{\mathcal{S}_{\infty}}(\boldsymbol{U }\boldsymbol{\cdot}\boldsymbol{n_\infty})\rho_1\boldsymbol{v}_1 \,{\rm d}S\right\rangle. } \end{align}

4. Expression of the radiation force for a slowly translating source

The final step is to compute this integral from the first-order acoustic field.

4.1. Pressure, density and velocity fields at first order

The first step to compute (3.16) is to determine the pressure, density and velocity fields at first order from the expression of the velocity potential determined previously in (2.21). First,

(4.1)\begin{equation} p_1=\frac{\partial \psi_1}{\partial t}=\frac{\left(1-\dfrac{1}{c_0}\,\dfrac{\partial R}{\partial t}\right)q'(t-R/c_0 )}{4{\rm \pi} R_1} -\frac{q(t-R/c_0 )\,\dfrac{\partial R_1}{\partial t}}{4{\rm \pi} R_1^2}. \end{equation}

Moreover, the coordinate of the velocity $v_{1i}$ along the direction $x_i = (x,y,z)$ is

(4.2)\begin{equation} v_{1x_i}={-}\frac{1}{\rho_0}\,\frac{\partial \psi_1}{\partial x_i}={-}\frac{1}{\rho_0}\left(\frac{-\dfrac1c_0\, \dfrac{\partial R}{\partial x_i}\,q'(t-R/c_0 )}{4{\rm \pi} R_1} -\frac{q(t-R/c_0 )\,\dfrac{\partial R_1}{\partial x_i}}{4{\rm \pi} R_1^2}\right). \end{equation}

Of course, we have $\rho _1 = p_1 / c_0^2$. Here, $R$ and $R_1$ are time- and space-dependent functions. To simplify the calculation of the derivatives and the force integral, we perform the change of variable corresponding to the Galilean transformation from $\mathcal {R}$ to $\mathcal {R}^*$:

(4.3a, 4.3b, 4.3c and 4.3d) \begin{cases}{} x^*=x-M c_0 t,\\ y^*=y,\\ z^*=z,\\ t^*=t.\end{cases}

Then $R_1$ and $R$ become

(4.4a,b)\begin{equation} R_1=\sqrt{{x^*}^2+({y^*}^2+{z^*}^2)(1-M ^2)} \quad\text{and}\quad R=\frac{M x^*+R_1}{1-M^2}. \end{equation}

The Jacobian matrix $J^*$ of this transformation is

(4.5)\begin{equation} J^*=\begin{pmatrix} 1 & 0 & 0 & -M c_0 \\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}, \quad\text{with}\ \det J^*=1. \end{equation}

We use the spherical coordinates $(r^*, \theta ^*, \varphi ^*)$ to compute the integral (see figure 3 for the notation):

(4.6a, 4.6b and 4.6c) \begin{cases}{} x^*=r^*\cos\theta^*,\\ y^*=r^*\sin\theta^*\cos\varphi^*,\\ z^*=r^*\sin\theta^*\sin\varphi^*. \end{cases}

The key point in the following derivation of the self-radiation force is that we consider $M\ll 1$, which means that the source translates at low velocity compared to the sound speed. This enables us to get simpler expressions of the pressure and velocity fields. First, we derive the expressions of $R_1$ and $R$ at first order in $M$:

(4.7)\begin{align} R_1 & =\sqrt{{r^*}^2-M ^2({y^*}^2+{z^*}^2)}= \sqrt{{r^*}^2-M ^2{r^*}^2\sin^2\theta^*} \nonumber\\ & \simeq r^*\left(1-\frac{M ^2}{2}\sin^2\theta^*\right)\simeq r^*+O(M) \end{align}

and

(4.8)\begin{equation} R\simeq\frac{M x^*+r^*\left(1-\dfrac{M^2}{2}\sin^2\theta^*\right)}{1-M^2}\simeq r^*+Mx^*. \end{equation}

In order to get the velocity and the pressure fields at first order in $M$, we compute at first the different time derivatives of $R_1$ and $R$:

(4.9)\begin{equation} \frac{\partial R}{\partial t}= \frac{\partial x^*}{\partial t}\,\frac{\partial R}{\partial x^*}+\frac{\partial t^*}{\partial t}\,\frac{\partial R}{\partial t^*}={-}M c_0 \left(\frac{\partial r^*}{\partial x^*}+M\right), \end{equation}

with

(4.10)\begin{equation} \frac{\partial r^*}{\partial x^*}=\frac{x^*}{r^*} = \cos \theta^*. \end{equation}

Hence we obtain

(4.11)\begin{equation} \frac{\partial R}{\partial t}={-}M c_0 (\cos\theta^*+M). \end{equation}

Then

(4.12)\begin{equation} \frac{\partial R_1}{\partial t}= \frac{\partial x^*}{\partial t}\,\frac{\partial R_1}{\partial x^*} +\frac{\partial t^*}{\partial t}\,\frac{\partial R_1}{\partial t^*}={-}M c_0 \cos\theta^*. \end{equation}

Finally, the acoustic pressure is

(4.13)\begin{equation} p_1=\frac{\left[1+M \left(\cos\theta^*+M \right)\right] q'(t-R/c_0 )}{4{\rm \pi} r^*} +\frac{q(t-R/c_0 )\,(M c_0 \cos\theta^*)}{4{\rm \pi} {r^*}^2}. \end{equation}

We choose a sphere $\mathcal {S}_{\infty }$ with radius $r_{\infty }$ huge compared to all the other lengths of the problem. We then write the acoustic pressure in the far-field approximation. At first order in $M$, we obtain

(4.14)\begin{equation} \boxed{ p_1=\frac{1+M \cos\theta^*}{4{\rm \pi} r^*}\,q'(t-R/c_0 ). } \end{equation}

In order to derive the velocity field, we compute the different space derivatives of $R_1$ and $R$:

(4.15a, 4.15b and 4.15c) \begin{cases}{} \frac{\partial R}{\partial x}=\frac{\partial x^*}{\partial x}\,\frac{\partial R}{\partial x^*}=\cos\theta^*+M,\\ \frac{\partial R}{\partial y}=\frac{\partial y^*}{\partial y}\,\frac{\partial R}{\partial y^*}=\sin\theta^*\cos\varphi^*,\\ \frac{\partial R}{\partial z}=\frac{\partial z^*}{\partial z}\, \frac{\partial R}{\partial z^*}=\sin\theta^*\sin\varphi^*, \end{cases}

and

(4.16)\begin{equation} \frac{\partial R_1}{\partial xi}= \frac{x_i^*}{r^*}. \end{equation}

We obtain

(4.17a, 4.17b and 4.17c) \begin{cases}{} v_{1x^*}=\frac{1}{\rho_0c_0}\left(\frac{(\cos\theta^*+M )\,q'(t-R/c_0 )}{4{\rm \pi} r^*} +c_0\,\frac{q(t-R/c_0 )}{4{\rm \pi} {r^*}^2} \,\frac{x^*}{r^*}\right),\\ v_{1y^*}=\frac{1}{\rho_0c_0}\left(\frac{\sin\theta^*\cos\varphi^*\,q'(t-R/c_0 )}{4{\rm \pi} r^*} + c_0\,\frac{q(t-R/c_0 )}{4{\rm \pi} {r^*}^2}\,\frac{y^*}{r^*}\right),\\ v_{1z^*}=\frac{1}{\rho_0c_0}\left(\frac{\sin\theta^*\sin\varphi^*\,q'(t-R/c_0 )}{4{\rm \pi} r^*} +c_0 \,\frac{q(t-R/c)}{4{\rm \pi} {r^*}^2}\,\frac{z^*}{r^*}\right). \end{cases}

We finally write the velocity field in the far-field approximation:

(4.18, 4.19 and 4.20) \begin{equation} \boxed{\begin{align} & v_{1x^*}=\frac{1}{\rho_0 c_0 }\,\frac{q'(t-R/c_0 )}{4{\rm \pi} r^*}\,(\cos\theta^*+M ),\\ & v_{1y^*}=\frac{1}{\rho_0 c_0 }\,\frac{q'(t-R/c_0 )}{4{\rm \pi} r^*}\sin\theta^*\cos\varphi^*,\\ & v_{1z^*}=\frac{1}{\rho_0 c_0 }\,\frac{q'(t-R/c_0 )}{4{\rm \pi} r^*}\sin\theta^*\sin\varphi^*.\end{align} } \end{equation}

Figure 3. We make the change of variables corresponding to the Galilean transformation from $\mathcal {R}$ to $\mathcal {R}^*$, and then use the local spherical coordinates $(r^*,\theta ^*,\varphi ^*)$.

4.2. Calculation of the integrals

With the change of variables (4.3a) and since the Jacobian of this change of variables is equal to 1, the integral expression of the radiation force (3.16) becomes

(4.21) \begin{align} \left\langle\boldsymbol{F}_{{rad}}\right\rangle&= \left\langle\iint_{\mathcal{S}_{\infty}^*}{\left[\left(\rho_0\,\frac{v_1^2}{2}-\frac{1}{\rho_0c_0^2}\,\frac{p_1^2}{2}\right) \bar{\bar{I}} -\rho_0\boldsymbol{v}_1\otimes\boldsymbol{v}_1\right]}\boldsymbol{n}^* \,{\rm d}S^*\right\rangle\nonumber\\ &\quad +\left\langle\iint_{\mathcal{S}_{\infty}^*}({U }\boldsymbol{\cdot}\boldsymbol{n_\infty}^*)\rho_1\boldsymbol{v}_1 \,{\rm d}S^*\right\rangle, \end{align}

with $\mathcal {S}_{\infty }^*$ the surface defined by $r^*=r_{\infty }^*$, a constant radius, the infinitesimal element of surface ${\rm d}S^*={r_{\infty }^*}^2\sin \theta ^* \,{\rm d}\theta ^* \,{\rm d}\varphi ^*$, $\theta ^* \in [0,{\rm \pi} ]$ and $\varphi ^*\in [0, 2 {\rm \pi}]$. Finally, $\boldsymbol {n}^* = \boldsymbol {n}_\infty ^* =\boldsymbol {e}_{r}^*$, with $(\boldsymbol {e}_{r}^*,\boldsymbol {e}_{\theta }^*,\boldsymbol {e}_{\varphi }^*)$ the spherical coordinates unit vector of $\mathcal {R}^*$. Since we have already expressed the pressure, velocity and density fields as a function of the spherical coordinates $(r^*, \theta ^*, \varphi ^*)$, we can now compute integral (4.21). In the following subsubsections, we compute separately each term of this integral.

4.2.1. Potential energy term

We have

(4.22)\begin{align} & \left\langle\iint_{\mathcal{S}_{\infty}^*}{\frac{1}{\rho_0 c_0 ^2}\,\frac{p_1^2}{2}}\,\boldsymbol{n}^*\,{\rm d}S^*\right\rangle \nonumber\\ &\quad = \left\langle\frac{1}{2\rho_0c_0^2}\int_{\varphi^*=0}^{2{\rm \pi}}\int_{\theta^*=0}^{\rm \pi}{\left[ \left(\frac{1+M \cos\theta^*}{4{\rm \pi} {r_{\infty}^*}}\right) q'(t-R/c_0 ) \right]^2}\boldsymbol{e}_{r}^*{r_{\infty}^*}^2\sin\theta^* \,{\rm d}\theta^* \,{\rm d}\varphi^*\right\rangle. \end{align}

The integration over $\varphi ^*$ along the $y^*$ and $z^*$ axes is null. Hence only the term along $x^*$ remains:

(4.23)\begin{align} &\left\langle\iint_{\mathcal{S}_{\infty}^*}{\frac{1}{\rho_0 c_0 ^2}\,\frac{p_1^2}{2} }\,\boldsymbol{n}^*\,{\rm d}S^*\right\rangle\nonumber\\ &\quad = \left\langle\frac{\rm \pi}{\rho_0c_0^2}\int_{0}^{\rm \pi}{\left[ \left(\frac{1+M \cos\theta^*}{4{\rm \pi} {r_{\infty}^*}}\right) q'(t-R/c_0 ) \right]^2}\cos\theta^*\sin\theta^*\,{\rm d}\theta^*\,\boldsymbol{x} \right\rangle . \end{align}

If we swap the time and space integrals, and since the function $q(t)$ is periodic, then we obtain

(4.24)\begin{equation} \left\langle\iint_{\mathcal{S}_{\infty}^*}{\frac{1}{\rho_0c_0^2}\,\frac{p_1^2}{2}}\,\boldsymbol{n}^*\,{\rm d}S^*\right\rangle= \frac{\left\langle q'(t)^2\right\rangle}{16{\rm \pi}\rho_0c_0^2}\int_{0}^{\rm \pi}{(1 +M \cos\theta^*)^2}\cos\theta^*\sin\theta^* \, {\rm d}\theta^*\,\boldsymbol{x}. \end{equation}

Since the last integral is equal to $4M/3$, we obtain

(4.25)\begin{equation} \boxed{ \left\langle\iint_{\mathcal{S}_{\infty}^*}{\frac{1}{\rho_0c_0^2}\,\frac{p_1^2}{2}}\,\boldsymbol{n}^*\,{\rm d}S^*\right\rangle= \frac{\left\langle q'^2\right\rangle M}{12{\rm \pi}\rho_0c_0^2}\,\boldsymbol{x}. } \end{equation}

4.2.2. Kinetic energy term

We have

(4.26)\begin{align} \left\langle\iint_{\mathcal{S}_{\infty}^*}{\rho_0\,\frac{v_1^2}{2}}\,\boldsymbol{n}^*\,{\rm d}S^*\right\rangle &=\left\langle\frac{1}{2\rho_0c_0^2}\int_{\varphi^*=0}^{2{\rm \pi}}\int_{\theta^*=0}^{\rm \pi} \left(\frac{q'(t-R/c_0)}{4{\rm \pi}{r_{\infty}^*}}\right)^2\right.\nonumber\\ &\quad \times \left.\vphantom{\frac{1}{2\rho_0c_0^2}} {\left((\cos\theta^*+M)^2+\sin^2\theta^*\right)}\boldsymbol{e}_{r}^*{r_{\infty}^*}^2\sin\theta^*\, {\rm d}\theta^*\,{\rm d}\varphi^*\right\rangle. \end{align}

Using the same arguments as previously, we have

(4.27)\begin{equation} \left\langle\iint_{\mathcal{S}_{\infty}^*}{\rho_0\,\frac{v_1^2}{2}}\,\boldsymbol{n}^*\,{\rm d}S^*\right\rangle= \frac{\left\langle q'^2\right\rangle}{16{\rm \pi}\rho_0 c_0 ^2}\int_0^{\rm \pi}{(1 + 2 M\cos\theta^* + M^2)}\cos\theta^*\sin\theta^*\,{\rm d}\theta^*\,\boldsymbol{x}. \end{equation}

Since the last integral is equal to $4M/3$, we obtain

(4.28)\begin{equation} \boxed{ \left\langle\iint_{\mathcal{S}_{\infty}^*}{\rho_0\,\frac{v_1^2}{2}}\,\boldsymbol{n}^*\,{\rm d}S^*\right\rangle= \frac{\left\langle q'^2\right\rangle M}{12{\rm \pi}\rho_0c_0^2}\,\boldsymbol{x} .} \end{equation}

4.2.3. Convective term

Due to the symmetry of the problem (invariance by rotation over angle $\varphi ^*$), no force can exist along the $\boldsymbol {y}$ and $\boldsymbol {z}$ directions. Hence we need only compute the following components of $\boldsymbol {v}_1\otimes \boldsymbol {v}_1$:

(4.29)\begin{equation} (v_{1x^*}^2) \boldsymbol{x} \otimes \boldsymbol{x} +(v_{1x^*}v_{1y^*}) \boldsymbol{x} \otimes \boldsymbol{y} +(v_{1x^*}v_{1z^*}) \boldsymbol{x} \otimes \boldsymbol{z}. \end{equation}

Then, due to the dependence of these terms over $\varphi ^*$ given in (4.18)–(4.20), and since $\boldsymbol {e}_r^* = \cos \theta ^* \boldsymbol {x} + \sin \theta ^* \cos \varphi ^* \boldsymbol {y} + \sin \theta ^* \sin \varphi ^* \boldsymbol {y}$, we obtain

(4.30)\begin{align} & \left\langle\iint_{\mathcal{S}_{\infty}^*}{\left[\rho_0\boldsymbol{v}_1\otimes\boldsymbol{v}_1 \right]}\boldsymbol{n}^* \,{\rm d}S^*\right\rangle \nonumber\\ &\quad = \frac{\left\langle q'^2\right\rangle}{8 {\rm \pi}\rho_0 c_0^2} \int_0^{\rm \pi}{ \left[ \left(\cos\theta^*+M\right)^2 \cos\theta^* + \left(\cos\theta^*+M\right) {\sin\theta^*}^2 \right]\sin\theta^* \,{\rm d}\theta^*}\,\boldsymbol{x}. \end{align}

The integral term is equal to $8M/3$, so

(4.31)\begin{equation} \boxed{ \left\langle\iint_{\mathcal{S}_{\infty}^*}{\left[\rho_0\boldsymbol{v}_1\otimes\boldsymbol{v}_1 \right]}\boldsymbol{n}^* \,{\rm d}S^*\right\rangle= \frac{\left\langle q'^2 \right\rangle M }{3{\rm \pi}\rho_0 c_0 ^2}v\boldsymbol{x} .} \end{equation}

4.2.4. Source translation term

The term due the translation of the sphere $\mathcal {S}_{\infty }$ is

(4.32)\begin{equation} \left\langle\iint_{\mathcal{S}_{\infty}^*}(\boldsymbol{U }\boldsymbol{\cdot}\boldsymbol{n_\infty^*})\rho_1\boldsymbol{v}_1 \,{\rm d}S^*\right\rangle = \frac{M\left\langle q'^2\right\rangle}{8{\rm \pi}\rho_0 c_0 ^2}\int_0^{\rm \pi}(1+M \cos\theta^*)(\cos\theta^*+M )\cos\theta^*\sin\theta^* \,{\rm d}\theta^*\,\boldsymbol{x}. \end{equation}

Since at leading order the last integral is equal to $2/3$, we finally obtain

(4.33)\begin{equation} \boxed{ \left\langle\iint_{\mathcal{S}_{\infty}^*}(\boldsymbol{U }\boldsymbol{\cdot}\boldsymbol{n_\infty})\rho_1\boldsymbol{v}_1 \,{\rm d}S^*\right\rangle= \frac{\left\langle q'^2\right\rangle M}{12{\rm \pi}\rho_0 c^2}\,\boldsymbol{x} .} \end{equation}

5. Final expression of the self-radiation force and discussion

5.1. Final expression of the self-radiation force

If we now replace (4.25), (4.28), (4.31) and (4.33) in (4.21), we obtain the final expression of the self-acoustic radiation force exerted on a monopolar source:

(5.1)\begin{equation} \boxed{ \left\langle\boldsymbol{F}_{{rad}}\right\rangle={-}\frac{\left\langle q'^2\right\rangle M}{4{\rm \pi}\rho_0 c_0 ^2}\,\boldsymbol{x}. } \end{equation}

There are many interesting things to notice in the above calculations and final expression. First, we see that the potential and kinetic energy terms cancel at leading order in $M$, so that the self-radiation force is due solely to the convective and translation terms. Second, the radiation force is proportional to the radiated intensity, and inversely proportional to the sound speed squared, which is classical in radiation force calculations. In addition, here the self-radiation force is proportional to the hydrodynamic Mach number $M$, which is expected since the force results from the asymmetry of the radiated field due to the translation of the source. Finally, and most importantly, $\left \langle \boldsymbol {F}_{{rad}}\right \rangle \boldsymbol {\cdot }\boldsymbol {U }$ is always negative, which means that this force always slows down the movement of the bubble.

5.2. An example of a monopolar oscillator: a vibrating bubble

In this subsection, we estimate this force for a translating and oscillating bubble in a liquid, which constitutes one example of an acoustic monopolar source. Indeed, bubbles are exceptional resonators, which exhibit strong monopolar resonances in the LWR. Let us consider a spherical bubble of mean radius $r_b$ in a liquid of density $\rho _0$ and sound speed $c_0$ vibrating periodically at its resonance frequency, called the Minnaert frequency:

(5.2)\begin{equation} \omega_M=\frac{1}{r_b}\sqrt{\frac{3\gamma p_0}{\rho_0}}, \end{equation}

with $\gamma$ the heat capacity ratio of the gas in the bubble, and $p_0$ the pressure of the surrounding fluid. At resonance, $\lambda /r_b={2{\rm \pi} c_0}/{\omega _M r_b}=2{\rm \pi} c_0 \sqrt {{\rho _0}/{3\gamma p_0}} \gg 1$ (of the order of $5 \times 10^2$ for an air bubble in water). Since the bubble is very small compared to the wavelength in this case, it can be considered as a point source a few wavelengths away from the bubble surface. The oscillation of this bubble creates a periodic mass flux $q(t) = Q \cos (\omega _M t)$, whose magnitude $Q$ is basically equal to the surface of the bubble $4{\rm \pi} r_b^2$, times the surrounding liquid mass density $\rho _0$, times the amplitude of the oscillations $\alpha r_b$ (where $\alpha$ designates a dimensionless parameter fixing the magnitude of the bubble oscillation), times the pulsation $\omega _b$:

(5.3)\begin{equation} Q \sim 4{\rm \pi} r_b^2\rho_0\alpha r_b\,\frac{1}{r_b}\sqrt{\frac{3\gamma p_0}{\rho_0}} = 4 {\rm \pi}r_b^2 \alpha \sqrt{3 \gamma p_0 \rho_0}. \end{equation}

Consequently, we have

(5.4)\begin{equation} \left\langle q'^2 \right\rangle \sim \tfrac{1}{2} \omega_M^2 Q^2 = 72 ({\rm \pi} \gamma p_0 \alpha r_b)^2 \end{equation}

and

(5.5)\begin{equation} |\langle\boldsymbol{F}_{{rad}}\rangle|=\frac{\left\langle q'^2\right\rangle }{4{\rm \pi}\rho_0 c_0 ^3}\,U \sim \frac{18 {\rm \pi}\gamma^2 p_0^2 \alpha^2 r_b^2}{\rho_0 c_0^3}\,U. \end{equation}

For small bubbles, it is interesting to compare this radiation force to the Stokes drag:

(5.6)\begin{equation} |\boldsymbol{F}_{{Sto}}|= C {\rm \pi}\mu r_b U, \end{equation}

with $C = 4$ for a bubble in a pure liquid moving at low Reynolds number, $C = 6$ if the surface is polluted so that the slip boundary condition is turned into a no-slip boundary condition (see e.g. Kim & Karilla 2005), and $C = 12$ for an undeformed bubble at large Reynolds numbers (see Moore 1963). If we compare (5.5) to (5.6), then we obtain

(5.7)\begin{equation} \frac{|\langle\boldsymbol{F}_{{rad}}\rangle|}{|\boldsymbol{F}_{\text{Sto}}|} \sim \frac{18}{C}\,\frac{\gamma^2 p_0^2\alpha^2 }{\mu\rho_0 c_0 ^3}\,r_b. \end{equation}

For a bubble rising in water at ambient temperature and pressure, we have $\rho _0 \sim 1\times 10^{3}\ {\rm kg}\ {\rm m}^{3}$, $\mu \sim 1\times 10^{-3}\ {\rm Pa}\ {\rm s}$, $c_0 \sim 1.5\times 10^{3}\ {\rm m}\ {\rm s}^{-1}$, $\gamma \sim 1.4$ and $p_0=1\times 10^{5}\ {\rm Pa}$, so that with $\alpha \sim 0.5$, we obtain

(5.8)\begin{equation} \frac{|\langle\boldsymbol{F}_{{rad}}\rangle|}{|\boldsymbol{F}_{{Sto}}|} \sim 7 m^{{-}1} \times r_b. \end{equation}

Hence the self-radiation force would be small compared to the Stokes drag for a millimetric bubble. However, the self-radiation force could become significant in cryogenic liquids such as liquid nitrogen or superfluid helium. In liquid nitrogen at $T\simeq 77\ {\rm K}$, we have $\rho _0=8\times 10^{2}\ {\rm kg}\ {\rm m}^{-3}$, $\mu =2\times 10^{-4}\ {\rm Pa}\ {\rm s}$, $c_0 =8\times 10^{2}\ {\rm m}\ {\rm s}^{-1}$, $\gamma \sim 1$ and $p_0=1\times 10^{5}\ {\rm Pa}$, so that for $\alpha \sim 0.5$, we obtain

(5.9)\begin{equation} \frac{|\langle\boldsymbol{F}_{{rad}}\rangle|}{|\boldsymbol{F}_{{Sto}}|} \sim 140 m^{{-}1} \times r_b, \end{equation}

which means that for a bubble of a few millimetres in radius, the two phenomena would be of the same orders of magnitude. Note first that this calculation constitutes a rough comparison of the radiation force and Stokes drag since (i) for large bubble oscillations, the bubble dynamics becomes nonlinear, and (ii) the Stokes drag is also modified by the bubble oscillations, as demonstrated by Magnaudet & Legendre (1998). Note also that the case of bubbles moving in a liquid constitutes just one possibility over the many configurations covered by (5.1) since the above theory applies for an arbitrary monopolar source moving in an arbitrary fluid as soon as (i) the monopolar source emits a signal in the LWR, and (ii) the source is moving at low speed compared to the sound speed.

6. Discussion, conclusion and perspectives

In this paper, we calculated the theoretical expression of the radiation force exerted on a translating monopolar source by its own acoustic field. We showed that the asymmetry of the radiated field due to the motion of the source creates a self-induced radiation force opposite to its motion. This theoretical work opens many perspectives: First, the self-radiation force could be measured in cryogenic liquids by studying the deviation of the rising speed of bubbles with and without forced oscillations. Second, this calculation could be extended (i) to different types of sources (different modes), (ii) to non-inviscid fluids, or finally (iii) to include an incident field. This could unveil some new physical effects of potential interest for subjects ranging from three-dimensional quantum analogues to acoustophoresis. Indeed, for (i), the force calculated here for a monopolar source is opposite to the source motion. But higher-order modes could lead to propulsive force instead, and hence to an object transported by its own wave. This would resonate with some recent experimental and theoretical investigations of essentially dipolar sources surfing on their own capillary waves by Ho et al. (2021) and Benham et al. (2022). For (ii), the fluid surrounding the source is considered as inviscid. It is well known that thermo-viscous effects can modify the radiation force due to the presence of a thermo-viscous boundary layer (see Doinikov 1997a,b,c; Settnes & Bruus 2012; Karlsen & Bruus 2015). This boundary layer essentially modifies the expression of the scattering coefficients that relate the phase and amplitude of the incident field to the one of the scattered field. In our calculation, the scattering coefficients do not appear since we did not consider any incident field. But thermo-viscous effects would appear when considering the response of the source to an external excitation. Thermo-viscous effects can also produce another nonlinear effect, called acoustic streaming. This streaming can result from dissipation in the boundary layer (in which case it is called ‘boundary Rayleigh streaming’) or from dissipation of the wave in the bulk (so-called ‘bulk Eckart streaming’). Nevertheless, for symmetry reasons, it is known that monopolar sources do not produce any acoustic streaming (see e.g. Doinikov et al. 2019). The streaming produced by an oscillating bubble generally results from parametric excitation of higher-order modes (see Cleve et al. 2019; Doinikov et al. 2019; Regnault et al. 2021), or asymmetries produced by the presence of a wall (Elder 1958; Marmottant & Hilgenfeldt 2003) or other bubbles (Meeki-Berrada et al. 2016; Combriat et al. 2018; Doinikov et al. 2022). Finally, for (iii) it is important to note that in the present calculation, only a wave emanating from the source is considered (there is no incident wave). Hence the source is supposed to be either activated by another type of field (not acoustic) – e.g. electromagnetic, gravity – or to be self-powered. In the case of acoustophoresis (see e.g. Petersson et al. 2007) and acoustic tweezers applications (see e.g. the review by Baudoin & Thomas 2020), objects are set into motion by external acoustic waves. Hence the adaptation of the present calculation to estimate the impact of the motion of the manipulated object on the experienced radiation force would require to add the effect of the incident wave to the present formalism.