Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-19T11:44:38.201Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-induced flapping dynamics of a flexible inverted foil in a uniform flow

Published online by Cambridge University Press:  28 September 2015

P. S. Gurugubelli  and
R. K. Jaiman
P. S. Gurugubelli
Affiliation:
Department of Mechanical Engineering, National University of Singapore, 117575, Singapore
R. K. Jaiman*
Affiliation:
Department of Mechanical Engineering, National University of Singapore, 117575, Singapore
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a numerical study on the self-induced flapping dynamics of an inverted flexible foil in a uniform flow. A high-order coupled fluid–structure solver based on fully coupled Navier–Stokes and nonlinear structural dynamic equations has been employed. Unlike a conventional flexible foil flapping where the leading edge is clamped, the inverted elastic foil is fixed at the trailing edge and the leading edge is allowed to oscillate freely. We investigate the evolution of flapping instability of an inverted foil as a function of the non-dimensional bending rigidity, 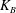$K_{B}$, Reynolds number, 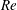$\mathit{Re}$, and structure-to-fluid mass ratio, 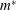$m^{\ast }$, and identify three distinct stability regimes, namely (i) fixed-point stable, (ii) deformed steady and (iii) unsteady flapping state. With the aid of a simplified analytical model, we show that the fixed-point stable regime loses its stability by static-divergence instability. The transition from the deformed steady state to the unsteady flapping regime is marked by a flow separation at the leading edge. We also show that an inverted foil is more vulnerable to static divergence than a conventional foil. Three distinct unsteady flapping modes have been observed as a function of decreasing 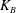$K_{B}$: (i) inverted limit-cycle oscillations, (ii) deformed flapping and (iii) flipped flapping. We characterize the transition to the deformed-flapping regime through a quasistatic equilibrium analysis between the structural restoring and the fluid forces. We further examine the effects of 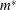$m^{\ast }$ on the post-critical flapping dynamics at a fixed 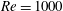$\mathit{Re}=1000$. Finally, we present the net work done by the fluid and the bending strain energy developed in a flexible foil due to the flapping motion. For small 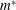$m^{\ast }$, we demonstrate that the flapping of an inverted flexible foil can generate 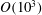$O(10^{3})$ times more strain energy in comparison to a conventional flexible foil flapping, which has a profound impact on energy harvesting devices.

JFM classification

Aerodynamics: Aerodynamics Instability: Parametric instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 781 , 25 October 2015 , pp. 657 - 694
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akcabay, D. T. & Young, Y. L. 2012 Hydroelastic response and energy harvesting potential of a flexible piezoelectric beam in viscous flow. Phys. Fluids 24, 054106.Google Scholar
Alben, S. 2009 Simulating the dynamics of flexible bodies and vortex sheets. J. Comput. Phys. 228 (7), 2587–2603.Google Scholar
Allen, J. J. & Smits, A. J. 2001 Energy harvesting eel. J. Fluids Struct. 15, 1–12.CrossRefGoogle Scholar
Antman, S. S. 1995 Nonlinear Problems of Elasticity. Springer.Google Scholar
Argentina, M. & Mahadevan, L. 2004 Fluid-flow-induced flutter of a flag. Proc. Natl Acad. Sci. USA 102, 1829–1834.Google Scholar
Bisplinghoff, R. L., Ashley, H. & Halfman, R. L. 1957 Aeroelasticity. Addison-Wesley.Google Scholar
Buchak, P., Eloy, C. & Reis, P. M. 2010 The clapping book: wind-driven oscillations in a stack of elastic sheets. Phys. Rev. Lett. 105, 194301.CrossRefGoogle Scholar
Connell, B. S. H. & Yue, D. K. P. 2007 Flapping dynamics of a flag in a uniform stream. J. Fluid Mech. 581, 33–67.CrossRefGoogle Scholar
Crandall, S. H., Dahl, N. C. & Lardner, T. J. 1995 An Introduction to the Mechanics of Solids. McGraw-Hill.Google Scholar
Datta, S. K. & Gottenberg, W. G. 1975 Instability of an elastic strip hanging in an airstream. J. Appl. Mech. 42, 195–198.Google Scholar
Dowell, E. H. 1966 Nonlinear oscillations of a fluttering plate. AIAA J. 4 (7), 1267–1275.Google Scholar
Dowell, E. H. 1970 Panel flutter: a review of the aeroelastic stability of plates and shells. AIAA J. 8 (3), 385–399.Google Scholar
Eloy, C., Kofman, N. & Schouveiler, L. 2012 The origin of hysteresis in the flag instability. J. Fluid Mech. 691, 583–593.Google Scholar
Eloy, C., Lagrange, R., Souilliez, C. & Schouveiler, L. 2008 Aeroelastic instability of cantilevered flexible plates in uniform flow. J. Fluid Mech. 611, 97–106.Google Scholar
Eloy, C., Souilliez, C. & Schouveiler, L. 2007 Flutter of a rectangular plate. J. Fluids Struct. 23 (6), 904–919.CrossRefGoogle Scholar
Farnell, D. J. J., David, T. & Barton, D. C. 2004 Numerical simulations of a filament in a flowing soap film. Intl J. Numer. Meth. Fluids 44, 313–330.CrossRefGoogle Scholar
Fung, Y. C. 1969 An Introduction to the Theory of Aeroelasticity. Dover.Google Scholar
Guo, C. Q. & Paidoussis, M. P. 2000 Stability of rectangular plates with free side-edges in two-dimensional inviscid channel flow. J. Appl. Mech. 67 (1), 171–176.Google Scholar
Huang, I., Rominger, J. & Nepf, H. 2011 The motion of kelp blades and surface renewal model. Limnol. Oceanogr. 56 (4), 1453–1462.Google Scholar
Huang, L. 1995 Flutter of cantilevered plates in axial flow. J. Fluids Struct. 9, 127–147.CrossRefGoogle Scholar
Jaiman, R. K., Loth, E. & Dutton, J. C. 2004 Simulations of normal shock-wave/boundary-layer interaction control using mesoflaps. AIAA J. Propul. Power 20, 344–352.CrossRefGoogle Scholar
Kim, D., Cossé, J., Huertas Cerdeira, C. & Gharib, M. 2013 Flapping dynamics of an inverted flag. J. Fluid Mech. 736, R1.Google Scholar
Kornecki, A., Dowell, E. H. & O’Brien, J. 1976 On the aeroelastic instability of two-dimensional panels in uniform incompressible flow. J. Sound Vib. 47 (2), 163–178.Google Scholar
Lighthill, M. J. 1960 Note on the swimming of slender fish. J. Fluid Mech. 9, 305–317.Google Scholar
Liu, J., Jaiman, R. K. & Gurugubelli, P. S. 2014 A stable second-order scheme for fluid–structure interaction with strong added-mass effects. J. Comput. Phys. 270, 687–710.Google Scholar
Lucey, A. D. 1998 The excitation of waves on a flexible panel in a uniform flow. Phil. Trans. R. Soc. Lond. A 356, 2999–3039.Google Scholar
Michelin, S. & Doare, O. 2013 Energy harvesting efficiency of piezoelectric flags in axial flows. J. Fluid Mech. 714, 489–504.Google Scholar
Michelin, S., Llewellyn Smith, S. G. & Glover, B. J. 2008 Vortex shedding model of a flapping flag. J. Fluid Mech. 617, 1–10.Google Scholar
Newman, J. N. 1977 Marine Hydrodynamics. MIT Press.Google Scholar
Ol, M. V. & Gharib, M. 2003 Leading-edge vortex structure of nonslender delta wings at low Reynolds numbers. AIAA J. 41 (1), 16–26.Google Scholar
Paidoussis, M. P. 2000 Fluid–Structure Interactions: Slender Structures and Axial Flow. Academic.Google Scholar
Schouveiler, L., Eloy, C. & Gal, P. L 2005 Flow-induced vibration of high mass ratio flexible filaments freely hanging in a flow. Phys. Fluids 17, 047104.CrossRefGoogle Scholar
Shelley, M., Vandenberghe, N. & Zhang, J. 2005 Heavy flags undergo spontaneous oscillations in flowing water. Phys. Rev. Lett. 94, 094302.Google Scholar
Shelley, M. J. & Zhang, J. 2011 Flapping and bending bodies interacting with fluid flows. Annu. Rev. Fluid Mech. 43 (1), 449–465.Google Scholar
Stein, K, Tezduyar, T. & Benney, R. 2003 Mesh moving techniques for fluid–structure interactions with large displacements. J. Appl. Mech. 70, 58–63.CrossRefGoogle Scholar
Taneda, S. 1968 Waving motions of flags. J. Phys. Soc. Japan 24, 392–401.CrossRefGoogle Scholar
Tang, L. & Paidoussis, M. P. 2007 On the instability and the post-critical behaviour of two-dimensional cantilevered flexible plates in axial-flow. J. Sound Vib. 305, 97–115.CrossRefGoogle Scholar
Tang, L., Paidoussis, M. P. & Jiang, J 2009 Cantilevered flexible plates in axial flow: energy transfer and the concept of flutter-mill. J. Sound Vib. 326, 263–276.Google Scholar
Temam, R. 2001 Navier–Stokes Equations. Theory and Numerical Analysis. AMS Chelsea.Google Scholar
Wang, Z. J. 2000 Two dimensional mechanism for insect hovering. Phys. Rev. Lett. 85 (10), 2216–2219.Google Scholar
Watanabe, Y., Isogai, K., Suzuki, S. & Sugihara, M 2002a A theoretical study of paper flutter. J. Fluids Struct. 16, 543–560.Google Scholar
Watanabe, Y., Suzuki, S., Sugihara, M. & Sueoka, Y. 2002b An experimental study of paper flutter. J. Fluids Struct. 16, 529–542.Google Scholar
Zhang, J., Childress, S., Libchaber, A. & Shelley, M. 2000 Flexible filaments in a flowing soap film as a model for one-dimensional flags in a two-dimensional wind. Nature 408, 835–839.Google Scholar
Zhu, L. & Peskin, C. S. 2002 Simulation of a flapping flexible filament in a flowing soap film by the immersed boundary method. J. Comput. Phys. 179, 452–468.Google Scholar
Zhu, L. & Peskin, C. S. 2003 Interaction of two flapping filaments in a flowing soap film. Phys. Fluids 15, 1954–1960.Google Scholar