Hostname: page-component-f554764f5-8cg97 Total loading time: 0 Render date: 2025-04-20T07:50:19.287Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-generated magnetic field in three-dimensional ablative Rayleigh–Taylor instability

Published online by Cambridge University Press:  04 December 2024

Dehua Zhang Open the ORCID record for Dehua Zhang [Opens in a new window] ,
Xian Jiang ,
Tao Tao ,
Jun Li Open the ORCID record for Jun Li [Opens in a new window] ,
Rui Yan Open the ORCID record for Rui Yan [Opens in a new window] ,
Dejun Sun  and
Jian Zheng
Dehua Zhang
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, PR China
Xian Jiang
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, PR China
Tao Tao
Affiliation:
Department of Plasma Physics and Fusion Engineering, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Jun Li
Affiliation:
Institute of Applied Physics and Computational Mathematics, Beijing 10094, PR China
Rui Yan*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, PR China IFSA Collaborative Innovation Center, Shanghai Jiao Tong University, Shanghai 200240, PR China
Dejun Sun
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, PR China
Jian Zheng
Affiliation:
Department of Plasma Physics and Fusion Engineering, University of Science and Technology of China, Hefei, Anhui 230026, PR China IFSA Collaborative Innovation Center, Shanghai Jiao Tong University, Shanghai 200240, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

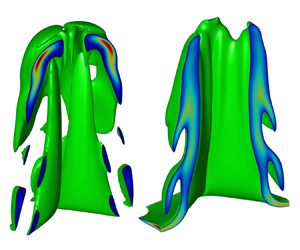
The self-generated magnetic field in three-dimensional (3-D) single-mode ablative Rayleigh–Taylor instability (ARTI) relevant to the acceleration phase of a direct-drive inertial confinement fusion (ICF) implosion is investigated. It is found that stronger magnetic fields up to a few thousand teslas can be generated by 3-D ARTI rather than by its two-dimensional (2-D) counterpart. The Nernst effects significantly alter the magnetic field convection and amplify the magnetic fields. The magnetic field of thousands of teslas yields the Hall parameter of the order of unity, leading to profound magnetized heat flux modification. While the magnetic field significantly accelerates the bubble growth in the short-wavelength 2-D modes through modifying the heat fluxes, the magnetic field mostly accelerates the spike growth but has little influence on the bubble growth in 3-D ARTI. The accelerated growth of spikes in 3-D ARTI is expected to enhance material mixing and degrade ICF implosion performance. This work is focused on a regime relevant to direct-drive ICF parameters at the National Ignition Facility, and it also covers a range of key parameters that are relevant to other ICF designs and hydrodynamic/astrophysical scenarios.

JFM classification

MHD and Electrohydrodynamics: Plasmas
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1000 , 10 December 2024 , A94
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abu-Shawareb, H., et al. 2022 Lawson criterion for ignition exceeded in an inertial fusion experiment. Phys. Rev. Lett. 129, 075001.CrossRefGoogle Scholar
Atzeni, S. & Meyer-ter-vehn, J. 2004 The Physics of Inertial Fusion. Oxford University Press.CrossRefGoogle Scholar
Bell, A.R. 1985 Non-Spitzer heat flow in a steadily ablating laser-produced plasma. Phys. Fluids 28 (6), 2007–2014.CrossRefGoogle Scholar
Betti, R., Goncharov, V.N., McCrory, R.L., Sorotokin, P. & Verdon, C.P. 1996 Self-consistent stability analysis of ablation fronts in inertial confinement fusion. Phys. Plasmas 3 (5), 2122–2128.CrossRefGoogle Scholar
Betti, R., Goncharov, V.N., McCrory, R.L. & Verdon, C.P. 1995 Self-consistent cutoff wave number of the ablative Rayleigh–Taylor instability. Phys. Plasmas 2 (10), 3844–3851.CrossRefGoogle Scholar
Betti, R., Goncharov, V.N., McCrory, R.L. & Verdon, C.P. 1998 Growth rates of the ablative Rayleigh–Taylor instability in inertial confinement fusion. Phys. Plasmas 5 (5), 1446–1454.CrossRefGoogle Scholar
Betti, R. & Sanz, J. 2006 Bubble acceleration in the ablative Rayleigh–Taylor instability. Phys. Rev. Lett. 97 (20), 205002.CrossRefGoogle ScholarPubMed
Bian, X., Aluie, H., Zhao, D., Zhang, H. & Livescu, D. 2020 Revisiting the late-time growth of single-mode Rayleigh–Taylor instability and the role of vorticity. Physica D 403, 132250.CrossRefGoogle Scholar
Bodner, S.E. 1974 Rayleigh–Taylor instability and laser-pellet fusion. Phys. Rev. Lett. 33 (13), 761.CrossRefGoogle Scholar
Braginskii, S.I. 1965 Transport processes in a plasma. Rev. Plasma Phys. 1, 205.Google Scholar
Briard, A., Gréa, B.-J. & Nguyen, F. 2022 Growth rate of the turbulent magnetic Rayleigh–Taylor instability. Phys. Rev. E 106, 065201.CrossRefGoogle ScholarPubMed
Briard, A., Gréa, B.-J. & Nguyen, F. 2024 Turbulent mixing in the vertical magnetic Rayleigh–Taylor instability. J. Fluid Mech. 979, A8.CrossRefGoogle Scholar
Burrows, A. 2000 Supernova explosions in the Universe. Nature 403 (6771), 727–733.CrossRefGoogle ScholarPubMed
Campbell, P.T., et al. 2022 Measuring magnetic flux suppression in high-power laser–plasma interactions. Phys. Plasmas 29 (1), 012701.CrossRefGoogle Scholar
Carlyle, J. & Hillier, A. 2017 The non-linear growth of the magnetic Rayleigh–Taylor instability. Astron. Astrophys. 605, A101.CrossRefGoogle Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Clarendon Press.Google Scholar
Chang, P.Y., Fiksel, G., Hohenberger, M., Knauer, J.P., Betti, R., Marshall, F.J., Meyerhofer, D.D., Séguin, F.H. & Petrasso, R.D. 2011 Fusion yield enhancement in magnetized laser-driven implosions. Phys. Rev. Lett. 107 (3), 035006.CrossRefGoogle ScholarPubMed
Craxton, R.S., et al. 2015 Direct-drive inertial confinement fusion: a review. Phys. Plasmas 22 (11), 110501.CrossRefGoogle Scholar
Cui, Y., Yang, X.-H., Ma, Y.-Y., Zhang, G.-B., Xu, B.-H., Chen, Z.-H., Li, Z., Shao, F.-Q. & Zhang, J. 2024 The importance of Righi–Leduc heat flux on the ablative Rayleigh–Taylor instability during a laser irradiating targets. High Power Laser Sci. Engng 12, e24.Google Scholar
Dahlburg, J.P., Gardner, J.H., Doolen, G.D. & Haan, S.W. 1993 The effect of shape in the three-dimensional ablative Rayleigh–Taylor instability. I. Single-mode perturbations. Phys. Fluids B: Plasma Phys. 5 (2), 571–584.CrossRefGoogle Scholar
Davies, J.R., et al. 2018 Laser entrance window transmission and reflection measurements for preheating in magnetized liner inertial fusion. Phys. Plasmas 25 (6), 062704.CrossRefGoogle Scholar
Davies, J.R., Wen, H., Ji, J.-Y. & Held, E.D. 2021 Transport coefficients for magnetic-field evolution in inviscid magnetohydrodynamics. Phys. Plasmas 28 (1), 012305.CrossRefGoogle Scholar
Egedal, J., Le, A. & Daughton, W. 2013 A review of pressure anisotropy caused by electron trapping in collisionless plasma, and its implications for magnetic reconnection. Phys. Plasmas 20 (6), 061201.CrossRefGoogle Scholar
Epperlein, E.M. & Haines, M.G. 1986 Plasma transport coefficients in a magnetic field by direct numerical solution of the Fokker–Planck equation. Phys. Fluids 29 (4), 1029–1041.CrossRefGoogle Scholar
Fu, J.Y., Zhang, H.S., Cai, H.B., Yao, P.L. & Zhu, S.P. 2023 a Effect of ablation on the nonlinear spike growth for the single-mode ablative Rayleigh–Taylor instability. Matter Radiat. Extrem. 8 (1), 016901.CrossRefGoogle Scholar
Fu, J.Y., Zhang, H.S., Cai, H.B. & Zhu, S.P. 2023 b Self-similar bubble-front evolutions of ablative Rayleigh–Taylor instability seeded by localized perturbations. Phys. Plasmas 30 (2), 022701.CrossRefGoogle Scholar
Gamezo, V.N., Khokhlov, A.M., Oran, E.S., Chtchelkanova, A.Y. & Rosenberg, R.O. 2003 Thermonuclear supernovae: simulations of the deflagration stage and their implications. Science 299 (5603), 77–81.CrossRefGoogle ScholarPubMed
Gao, L., et al. 2013 Observation of self-similarity in the magnetic fields generated by the ablative nonlinear Rayleigh–Taylor instability. Phys. Rev. Lett. 110 (18), 185003.CrossRefGoogle ScholarPubMed
Gao, L., Nilson, P.M., Igumenshchev, I.V., Haines, M.G., Froula, D.H., Betti, R. & Meyerhofer, D.D. 2015 Precision mapping of laser-driven magnetic fields and their evolution in high-energy-density plasmas. Phys. Rev. Lett. 114 (21), 215003.CrossRefGoogle ScholarPubMed
Gao, L., Nilson, P.M., Igumenschev, I.V., Hu, S.X., Davies, J.R., Stoeckl, C., Haines, M.G., Froula, D.H., Betti, R. & Meyerhofer, D.D. 2012 Magnetic field generation by the Rayleigh–Taylor instability in laser-driven planar plastic targets. Phys. Rev. Lett. 109 (11), 115001.CrossRefGoogle ScholarPubMed
García-Rubio, F., Betti, R., Sanz, J. & Aluie, H. 2021 Magnetic-field generation and its effect on ablative Rayleigh–Taylor instability in diffusive ablation fronts. Phys. Plasmas 28 (1), 012103.CrossRefGoogle Scholar
Gomez, M.R., et al. 2014 Experimental demonstration of fusion-relevant conditions in magnetized liner inertial fusion. Phys. Rev. Lett. 113 (15), 155003.CrossRefGoogle ScholarPubMed
Goncharov, V.N. 2002 Analytical model of nonlinear, single-mode, classical Rayleigh–Taylor instability at arbitrary Atwood numbers. Phys. Rev. Lett. 88, 134502.CrossRefGoogle ScholarPubMed
Goncharov, V.N., Betti, R., McCrory, R.L., Sorotokin, P. & Verdon, C.P. 1996 a Self-consistent stability analysis of ablation fronts with large Froude numbers. Phys. Plasmas 3 (4), 1402–1414.CrossRefGoogle Scholar
Goncharov, V.N., Betti, R., McCrory, R.L. & Verdon, C.P. 1996 b Self-consistent stability analysis of ablation fronts with small Froude numbers. Phys. Plasmas 3 (12), 4665–4676.CrossRefGoogle Scholar
Grea, B.-J. & Briard, A. 2023 Inferring the magnetic field from the Rayleigh–Taylor instability. Astrophys. J. 958 (2), 164.CrossRefGoogle Scholar
Gregori, G., et al. 2012 Generation of scaled protogalactic seed magnetic fields in laser-produced shock waves. Nature 481 (7382), 480–483.CrossRefGoogle ScholarPubMed
Gregori, G., Reville, B. & Miniati, F. 2015 The generation and amplification of intergalactic magnetic fields in analogue laboratory experiments with high power lasers. Phys. Rep. 601, 1–34 .CrossRefGoogle Scholar
Haines, M.G. 1985 Magnetic-field generation in laser fusion and hot-electron transport. Can. J. Phys. 64 (8), 912–919.CrossRefGoogle Scholar
Harten, A., Lax, P.D. & van Leer, B. 1983 On upstream differencing and Godunov-type schemes for hyperbolic conservation laws. SIAM Rev. 25 (1), 35–61.CrossRefGoogle Scholar
He, X., Zhang, R., Chen, S. & Doolen, G.D. 1999 On the three-dimensional Rayleigh–Taylor instability. Phys. Fluids 11 (5), 1143–1152.CrossRefGoogle Scholar
Hecht, J., Ofer, D., Alon, U., Shvarts, D., Orszag, S.A., Shvarts, D. & McCrory, R.L. 1995 Three-dimensional simulations and analysis of the nonlinear stage of the Rayleigh–Taylor instability. Laser Part. Beams 13 (3), 423–440.CrossRefGoogle Scholar
Huba, J.D. 1998 NRL Plasma Formulary, vol. 6790. Naval Research Laboratory.Google Scholar
Ikegawa, T. & Nishihara, K. 2002 Ablation effects on weakly nonlinear Rayleigh–Taylor instability with a finite bandwidth. Phys. Rev. Lett. 89, 115001.CrossRefGoogle ScholarPubMed
Jacobs, J.W. & Catton, I. 1988 Three-dimensional Rayleigh–Taylor instability. Part 2. Experiment. J. Fluid Mech. 187, 353–371.CrossRefGoogle Scholar
Ji, J.-Y. & Held, E.D. 2013 Closure and transport theory for high-collisionality electron–ion plasmas. Phys. Plasmas 20 (4), 042114.CrossRefGoogle Scholar
Jun, B.-I., Norman, M.L. & Stone, J.M. 1995 A numerical study of Rayleigh–Taylor instability in magnetic fluids. Astrophys. J. 453, 332.CrossRefGoogle Scholar
Kopp, M.I. & Yanovsky, V.V. 2024 Generation of large-scale magnetic-vortex structures in stratified magnetized plasma by a small-scale force. Phys. Plasmas 31 (8), 082301.CrossRefGoogle Scholar
Layzer, D. 1955 On the instability of superposed fluids in a gravitational field. Astrophys. J. 122, 1.CrossRefGoogle Scholar
van Leer, B. 1984 On the relation between the upwind-differencing schemes of Godunov, Engquist–Osher and Roe. SIAM J. Sci. Stat. Comput. 5 (1), 1–20.CrossRefGoogle Scholar
Li, C.K., et al. 2007 Observation of the decay dynamics and instabilities of megagauss field structures in laser-produced plasmas. Phys. Rev. Lett. 99 (1), 015001.Google ScholarPubMed
Li, C.K., et al. 2009 Proton radiography of dynamic electric and magnetic fields in laser-produced high-energy-density plasmas. Phys. Plasmas 16 (5), 056304.CrossRefGoogle Scholar
Li, J., Yan, R., Zhao, B., Wu, J., Wang, L. & Zou, S. 2024 Effect of hot-electron preheating on the multimode bubble-front growth of the ablative Rayleigh–Taylor instability. Phys. Plasmas 31 (1), 012703.CrossRefGoogle Scholar
Li, J., Yan, R., Zhao, B., Zheng, J., Zhang, H. & Lu, X. 2022 Mitigation of the ablative Rayleigh–Taylor instability by nonlocal electron heat transport. Matter Radiat. Extrem. 7 (5), 055902.CrossRefGoogle Scholar
Li, J., Yan, R., Zhao, B., Zheng, J., Zhang, H. & Lu, X. 2023 Role of hot electrons in mitigating ablative Rayleigh–Taylor instability. Phys. Plasmas 30 (2), 022706.CrossRefGoogle Scholar
Lindl, J. 1995 Development of the indirect-drive approach to inertial confinement fusion and the target physics basis for ignition and gain. Phys. Plasmas 2 (11), 3933–4024.CrossRefGoogle Scholar
Lindl, J.D. 1998 Inertial Confinement Fusion. Springer New York.Google Scholar
Lindl, J.D., Amendt, P., Berger, R.L., Glendinning, S.G., Glenzer, S.H., Haan, S.W., Kauffman, R.L., Landen, O.L. & Suter, L.J. 2004 The physics basis for ignition using indirect-drive targets on the National Ignition Facility. Phys. Plasmas 11 (2), 339–491.CrossRefGoogle Scholar
Liu, Y., Zhang, D.-H., Xin, J.-F., Pu, Y., Li, J., Tao, T., Sun, D., Yan, R. & Zheng, J. 2023 Growth of ablative Rayleigh–Taylor instability induced by time-varying heat-flux perturbation. Matter Radiat. Extrem. 9 (1), 016603.CrossRefGoogle Scholar
Manuel, M.J.-E., et al. 2012 a First measurements of Rayleigh–Taylor-induced magnetic fields in laser-produced plasmas. Phys. Rev. Lett. 108 (25), 255006.CrossRefGoogle ScholarPubMed
Manuel, M.J.-E., et al. 2012 b Rayleigh–Taylor-induced magnetic fields in laser-irradiated plastic foils. Phys. Plasmas 19 (8), 082710.CrossRefGoogle Scholar
Manuel, M.J.-E., et al. 2015 Collisional effects on Rayleigh–Taylor-induced magnetic fields. Phys. Plasmas 22 (5), 056305.CrossRefGoogle Scholar
Matsuo, K., Sano, T., Nagatomo, H., Somekawa, T., Law, K.F.F., Morita, H., Arikawa, Y. & Fujioka, S. 2021 Enhancement of ablative Rayleigh–Taylor instability growth by thermal conduction suppression in a magnetic field. Phys. Rev. Lett. 127 (16), 165001.CrossRefGoogle ScholarPubMed
McKenty, P.W., Goncharov, V.N., Town, R.P.J., Skupsky, S., Betti, R. & McCrory, R.L. 2001 Analysis of a direct-drive ignition capsule designed for the National Ignition Facility. Phys. Plasmas 8 (5), 2315.CrossRefGoogle Scholar
Mima, K., Tajima, T. & Leboeuf, J.N. 1978 Magnetic field generation by the Rayleigh–Taylor instability. Phys. Rev. Lett. 41 (25), 1715–1719.CrossRefGoogle Scholar
Moody, J.D., et al. 2022 a The magnetized indirect drive project on the National Ignition Facility. J. Fusion Energy 41, 7.CrossRefGoogle Scholar
Moody, J.D., et al. 2022 b Increased ion temperature and neutron yield observed in magnetized indirectly driven D$_2$-filled capsule implosions on the National Ignition Facility. Phys. Rev. Lett. 129 (19), 195002.CrossRefGoogle Scholar
Nishiguchi, A., Yabe, T. & Haines, M.G. 1985 Nernst effect in laser-produced plasmas. Phys. Fluids 28 (12), 3683–3690.CrossRefGoogle Scholar
Nishiguchi, A., Yabe, T., Haines, M.G., Psimopoulos, M. & Takewaki, H. 1984 Convective amplification of magnetic fields in laser-produced plasmas by the Nernst effect. Phys. Rev. Lett. 53 (3), 262–265.CrossRefGoogle Scholar
Perkins, L.J., Ho, D.D.M., Logan, B.G., Zimmerman, G.B., Rhodes, M.A., Strozzi, D.J., Blackfield, D.T. & Hawkins, S.A. 2017 The potential of imposed magnetic fields for enhancing ignition probability and fusion energy yield in indirect-drive inertial confinement fusion. Phys. Plasmas 24 (6), 062708.CrossRefGoogle Scholar
Piriz, A.R., Sanz, J. & Ibañez, L.F. 1997 Rayleigh–Taylor instability of steady ablation fronts: the discontinuity model revisited. Phys. Plasmas 4 (4), 1117–1126.CrossRefGoogle Scholar
Raven, A., Willi, O. & Rumsby, P.T. 1978 Megagauss magnetic field profiles in laser-produced plasmas. Phys. Rev. Lett. 41 (8), 554–557.CrossRefGoogle Scholar
Rayleigh, Lord 1900 Scientific Papers II, p. 200. Cambridge University Press.Google Scholar
Sadler, J.D., Walsh, C.A. & Li, H. 2021 Symmetric set of transport coefficients for collisional magnetized plasma. Phys. Rev. Lett. 126, 075001.CrossRefGoogle ScholarPubMed
Sadler, J.D., Walsh, C.A., Zhou, Y. & Li, H. 2022 Role of self-generated magnetic fields in the inertial fusion ignition threshold. Phys. Plasmas 29 (7), 072701.CrossRefGoogle Scholar
Sanz, J. 1994 Self-consistent analytical model of the Rayleigh–Taylor instability in inertial confinement fusion. Phys. Rev. Lett. 73 (2700–2703), 1919–1922.CrossRefGoogle ScholarPubMed
Shneerson, G.A., Dolotenko, M.I. & Krivosheev, S.I. 2014 Strong and Superstrong Pulsed Magnetic Fields Generation. Walter de Gruyter GmbH & Co KG.CrossRefGoogle Scholar
Sio, H., et al. 2023 Performance scaling with an applied magnetic field in indirect-drive inertial confinement fusion implosions. Phys. Plasmas 30 (7), 072709.CrossRefGoogle Scholar
Slutz, S.A. & Vesey, R.A. 2012 High-gain magnetized inertial fusion. Phys. Rev. Lett. 108 (2), 025003.CrossRefGoogle ScholarPubMed
Spitzer, L. & Härm, R. 1953 Transport phenomena in a completely ionized gas. Phys. Rev. 89, 977–981.CrossRefGoogle Scholar
Srinivasan, B., Dimonte, G. & Tang, X.Z. 2012 Magnetic field generation in Rayleigh–Taylor unstable inertial confinement fusion plasmas. Phys. Rev. Lett. 108 (16), 165002.CrossRefGoogle ScholarPubMed
Srinivasan, B. & Tang, X.Z. 2012 Mechanism for magnetic field generation and growth in Rayleigh–Taylor unstable inertial confinement fusion plasmas. Phys. Plasmas 19 (8), 082703.CrossRefGoogle Scholar
Srinivasan, B. & Tang, X.Z. 2013 The mitigating effect of magnetic fields on Rayleigh–Taylor unstable inertial confinement fusion plasmas. Phys. Plasmas 20 (5), 056307.CrossRefGoogle Scholar
Stamper, J.A. 1991 Review on spontaneous magnetic fields in laser-produced plasmas: phenomena and measurements. Laser Part. Beams 9 (4), 841–862.CrossRefGoogle Scholar
Stamper, J.A., McLean, E.A. & Ripin, B.H. 1978 Studies of spontaneous magnetic fields in laser-produced plasmas by Faraday rotation. Phys. Rev. Lett. 40 (18), 1177–1181.CrossRefGoogle Scholar
Stamper, J.A., Papadopoulos, K., Sudan, R.N., Dean, S.O., McLean, E.A. & Dawson, J.M. 1971 Spontaneous magnetic fields in laser-produced plasmas. Phys. Rev. Lett. 26 (17), 1012–1015.CrossRefGoogle Scholar
Stamper, J.A. & Ripin, B.H. 1975 Faraday-rotation measurements of megagauss magnetic fields in laser-produced plasmas. Phys. Rev. Lett. 34 (3), 138–141.CrossRefGoogle Scholar
Stone, J.M. & Gardiner, T. 2007 a The magnetic Rayleigh–Taylor instability in three dimensions. Astrophys. J. 671 (2), 1726.CrossRefGoogle Scholar
Stone, J.M. & Gardiner, T. 2007 b Nonlinear evolution of the magnetohydrodynamic Rayleigh–Taylor instability. Phys. Fluids 19 (9), 094104.CrossRefGoogle Scholar
Strang, G. 1968 On the construction and comparison of difference schemes. SIAM J. Numer. Anal. 5 (3), 506–517.CrossRefGoogle Scholar
Takabe, H., Mima, K., Montierth, L. & Morse, R.L. 1985 Self-consistent growth rate of the Rayleigh–Taylor instability in an ablatively accelerating plasma. Phys. Fluids 28 (12), 3676–3682.CrossRefGoogle Scholar
Tapinou, K.C., Wheatley, V., Bond, D. & Jahn, I. 2023 The effect of collisions on the multi-fluid plasma Richtmyer–Meshkov instability. Phys. Plasmas 30 (2), 022707.CrossRefGoogle Scholar
Taylor, G. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. i. Proc. R. Soc. Lond. 201 (1065), 192–196.Google Scholar
Tubman, E.R., et al. 2021 Observations of pressure anisotropy effects within semi-collisional magnetized plasma bubbles. Nat. Commun. 12 (1), 334.CrossRefGoogle ScholarPubMed
Tzeferacos, P., et al. 2018 Laboratory evidence of dynamo amplification of magnetic fields in a turbulent plasma. Nat. Commun. 9 (1), 591.CrossRefGoogle Scholar
Velikovich, A.L., Giuliani, J.L. & Zalesak, S.T. 2019 Nernst thermomagnetic waves in magnetized high energy density plasmas. Phys. Plasmas 26 (11), 112702.CrossRefGoogle Scholar
Wagner, U., et al. 2004 Laboratory measurements of 0.7 GG magnetic fields generated during high-intensity laser interactions with dense plasmas. Phys. Rev. E 70 (2), 026401.CrossRefGoogle ScholarPubMed
Walsh, C.A. 2022 Magnetized ablative Rayleigh–Taylor instability in three dimensions. Phys. Rev. E 105 (2), 025206.CrossRefGoogle ScholarPubMed
Walsh, C.A., Chittenden, J.P., McGlinchey, K., Niasse, N.P.L. & Appelbe, B.D. 2017 Self-generated magnetic fields in the stagnation phase of indirect-drive implosions on the National Ignition Facility. Phys. Rev. Lett. 118, 155001.CrossRefGoogle ScholarPubMed
Wang, L.F., Ye, W.H., Sheng, Z.M., Don, W.-S., Li, Y.J. & He, X.T. 2010 Preheating ablation effects on the Rayleigh–Taylor instability in the weakly nonlinear regime. Phys. Plasmas 17 (12), 122706.CrossRefGoogle Scholar
Wei, T. & Livescu, D. 2012 Late-time quadratic growth in single-mode Rayleigh–Taylor instability. Phys. Rev. E 86, 046405.CrossRefGoogle ScholarPubMed
Wurden, G.A., et al. 2016 Magneto-inertial fusion. J. Fusion Energy 35 (1), 69–77.CrossRefGoogle Scholar
Xin, J., Liu, Y., Jiang, X., Yan, R., Li, J., Wan, Z.-H., Sun, D.-J. & Zheng, J. 2023 Effects of ablation velocity on ablative Rayleigh–Taylor instability. Phys. Plasmas 30 (11), 112702.CrossRefGoogle Scholar
Xin, J., Yan, R., Wan, Z.H., Sun, D.J., Zheng, J., Zhang, H., Aluie, H. & Betti, R. 2019 Two mode coupling of the ablative Rayleigh–Taylor instabilities. Phys. Plasmas 26 (3), 032703.CrossRefGoogle Scholar
Yan, R., Betti, R., Sanz, J., Aluie, H., Liu, B. & Frank, A. 2016 Three-dimensional single-mode nonlinear ablative Rayleigh–Taylor instability. Phys. Plasmas 23 (2), 022701.CrossRefGoogle Scholar
Zhang, D., Li, J., Xin, J., Yan, R., Wan, Z., Zhang, H. & Zheng, J. 2022 Self-generated magnetic field in ablative Rayleigh–Taylor instability. Phys. Plasmas 29 (7), 072702.CrossRefGoogle Scholar
Zhang, H., Betti, R., Yan, R. & Aluie, H. 2020 Nonlinear bubble competition of the multimode ablative Rayleigh–Taylor instability and applications to inertial confinement fusion. Phys. Plasmas 27 (12), 122701.CrossRefGoogle Scholar
Zhang, H., Betti, R., Yan, R., Zhao, D., Shvarts, D. & Aluie, H. 2018 Self-similar multimode bubble-front evolution of the ablative Rayleigh–Taylor instability in two and three dimensions. Phys. Rev. Lett. 121 (18), 185002.CrossRefGoogle ScholarPubMed
Zylstra, A.B., et al. 2022 Burning plasma achieved in inertial fusion. Nature 601 (7894), 542–548.CrossRefGoogle ScholarPubMed