Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gennaro, E. M.
Souza, B. D. P.
and
Rodríguez, D.
2019.
The effect of compressibility on the primary global instability of unforced laminar separation bubbles.
Journal of the Brazilian Society of Mechanical Sciences and Engineering,
Vol. 41,
Issue. 12,
Xu, Dongdong
and
Wu, Xuesong
2021.
Elevated low-frequency free-stream vortical disturbances eliminate boundary-layer separation.
Journal of Fluid Mechanics,
Vol. 920,
Issue. ,
Kusama, Kensuke
Nagata, Takayuki
Anyoji, Masayuki
Nonomura, Taku
and
Asai, Keisuke
2021.
Investigation of Mach number effects on flow over a flat plate at Reynolds number of 1.0 × 104 by schlieren visualization .
Fluid Dynamics Research,
Vol. 53,
Issue. 1,
p.
015513.
Martini, Eduardo
Rodríguez, Daniel
Towne, Aaron
and
Cavalieri, André V.G.
2021.
Efficient computation of global resolvent modes.
Journal of Fluid Mechanics,
Vol. 919,
Issue. ,
Rodriguez, Daniel
Martini, Eduardo
Cavalieri, Andrè
and
Jordan, Peter
2021.
On the relation between the self-excited three-dimensionality of laminar separation bubbles and their receptivity to external disturbances.
Xia, Tianyu
Dong, Hao
Yang, Liming
Liu, Shicheng
and
Jin, Zhou
2021.
Investigation on flow structure and aerodynamic characteristics over an airfoil at low Reynolds number—A review.
AIP Advances,
Vol. 11,
Issue. 5,
Khobragade, Nikhil
Unnikrishnan, S.
and
Kumar, Rajan
2021.
Linear and Nonlinear Flow Analysis of Elements of a Supersonic Inlet.
AIAA Journal,
Vol. 59,
Issue. 11,
p.
4392.
Jiang, Si-Ya
and
Fu, Song
2022.
Investigation on spatial evolutions of two- and three-dimensional modes in a laminar separation bubble over a low-pressure turbine cascade.
Physics of Fluids,
Vol. 34,
Issue. 1,
Bugeat, B.
Robinet, J.-Ch.
Chassaing, J.-C.
and
Sagaut, P.
2022.
Low-frequency resolvent analysis of the laminar oblique shock wave/boundary layer interaction.
Journal of Fluid Mechanics,
Vol. 942,
Issue. ,
Ma, Xingyu
Tang, Zhanqi
and
Jiang, Nan
2022.
Experimental study of self-sustained spanwise streaks and turbulent mixing in separated shear flow.
International Journal of Heat and Fluid Flow,
Vol. 96,
Issue. ,
p.
109012.
Gowree, E.R.
Jaroslawski, T.
Mellot, B.
and
Gojon, R.
2023.
Noise reduction on low Reynolds number rotors by boundary layer transition.
Applied Acoustics,
Vol. 210,
Issue. ,
p.
109446.
Fava, T. C. L.
Lobo, B. A.
Nogueira, P. A. S.
Schaffarczyk, A. P.
Breuer, M.
Henningson, D. S.
and
Hanifi, A.
2023.
Numerical study of the hydrodynamic stability of a wind-turbine airfoil with a laminar separation bubble under free-stream turbulence.
Physics of Fluids,
Vol. 35,
Issue. 8,
Jaroslawski, Tomek
Forte, Maxime
Vermeersch, Olivier
Moschetta, Jean-Marc
and
Gowree, Erwin R.
2023.
Disturbance growth in a laminar separation bubble subjected to free-stream turbulence.
Journal of Fluid Mechanics,
Vol. 956,
Issue. ,
Niessen, Sébastien E. M.
Groot, Koen J.
Hickel, Stefan
and
Terrapon, Vincent E.
2023.
Convective instabilities in a laminar shock-wave/boundary-layer interaction.
Physics of Fluids,
Vol. 35,
Issue. 2,
Mohamed Aniffa, S.
Caesar, V.S.
Dabaria, V.
and
Mandal, A.C.
2023.
Characteristics of geometry-and pressure-induced laminar separation bubbles at an enhanced level of free-stream turbulence.
Journal of Fluid Mechanics,
Vol. 957,
Issue. ,
Aniffa, S. Mohamed
and
Mandal, Alakesh Ch.
2023.
Experiments on the unsteady massive separation over an aerofoil.
Physical Review Fluids,
Vol. 8,
Issue. 12,
Dellacasagrande, M.
Lengani, D.
Simoni, D.
and
Yarusevych, S.
2023.
A data-driven analysis of short and long laminar separation bubbles.
Journal of Fluid Mechanics,
Vol. 976,
Issue. ,
Klotz, L.
Bukowski, K.
and
Gumowski, K.
2024.
Influence of porous material on the flow behind a backward-facing step: experimental study.
Journal of Fluid Mechanics,
Vol. 998,
Issue. ,
Fava, T. C. L.
Henningson, D. S.
and
Hanifi, A.
2024.
Boundary layer stability on a rotating wind turbine blade section.
Physics of Fluids,
Vol. 36,
Issue. 9,
Marbona, Himpu
Rodríguez, Daniel
Martínez-Cava, Alejandro
and
Valero, Eusebio
2024.
Impact of harmonic inflow variations on the size and dynamics of the separated flow over a bump.
Physical Review Fluids,
Vol. 9,
Issue. 5,
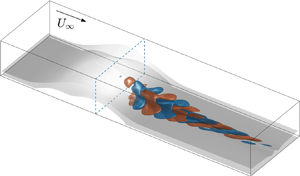
 $7\,\%$ of the free-stream velocity, well below the
$7\,\%$ of the free-stream velocity, well below the  ${\approx } 16\,\%$ required for the absolute instability of Kelvin–Helmholtz waves. Direct numerical simulations are used to describe the nonlinear evolution of the primary instability, which is found to correspond to a supercritical pitchfork bifurcation and results in fully three-dimensional flows with spanwise inhomogeneity of finite amplitude. An extension of the classic weakly non-parallel analysis is then applied to the bifurcated flows, that have a strong dependence on the cross-stream planes and a mild dependence on the streamwise direction. The spanwise distortion of the separated flow induced by the primary instability is found to strongly destabilize the Kelvin–Helmholtz waves, leading to their absolute instability and the appearance of a global oscillator-type instability. This sequence of instabilities triggers the laminar–turbulent transition without requiring external disturbances or actuation. The characteristic frequency and streamwise and spanwise wavelengths of the self-excited instability are in good agreement with those reported for low-turbulence wind-tunnel experiments without explicit forcing. This indicates that the inherent dynamics described by the self-excited instability can also be relevant when external disturbances are present.
${\approx } 16\,\%$ required for the absolute instability of Kelvin–Helmholtz waves. Direct numerical simulations are used to describe the nonlinear evolution of the primary instability, which is found to correspond to a supercritical pitchfork bifurcation and results in fully three-dimensional flows with spanwise inhomogeneity of finite amplitude. An extension of the classic weakly non-parallel analysis is then applied to the bifurcated flows, that have a strong dependence on the cross-stream planes and a mild dependence on the streamwise direction. The spanwise distortion of the separated flow induced by the primary instability is found to strongly destabilize the Kelvin–Helmholtz waves, leading to their absolute instability and the appearance of a global oscillator-type instability. This sequence of instabilities triggers the laminar–turbulent transition without requiring external disturbances or actuation. The characteristic frequency and streamwise and spanwise wavelengths of the self-excited instability are in good agreement with those reported for low-turbulence wind-tunnel experiments without explicit forcing. This indicates that the inherent dynamics described by the self-excited instability can also be relevant when external disturbances are present.


