Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T17:38:31.989Z Has data issue: false hasContentIssue false
  • English
  • Français

Sedimentation of a sphere in a viscoelastic fluid: a multiscale simulation approach

Published online by Cambridge University Press:  18 January 2012

A. Abedijaberi  and
B. Khomami
A. Abedijaberi
Affiliation:
Material Research & Innovation Laboratory (MRAIL), Department of Chemical & Biomolecular Engineering, University of Tennessee in Knoxville, Knoxville, TN 37996-5334, USA
B. Khomami*
Affiliation:
Material Research & Innovation Laboratory (MRAIL), Department of Chemical & Biomolecular Engineering, University of Tennessee in Knoxville, Knoxville, TN 37996-5334, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A long-standing problem in non-Newtonian fluid mechanics, namely the relationship between drag experienced by a sphere settling in a tube filled with a dilute polymeric solution and the sphere sedimentation velocity, is investigated via self-consistent multiscale flow simulations. Comparison with experimental measurements by Arigo et al. (J. Non-Newtonian Fluid Mech., vol. 60, 1995, pp. 225–257) have revealed that the evolution of the drag coefficient as a function of fluid elasticity can be accurately predicted when the macromolecular dynamics is described by realistic micromechanical models that closely capture the transient extensional viscosity of the experimental fluid at high extension rates. 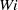Specifically, for the first time we have computed the drag coefficient on the sphere at high Weissenberg number utilizing multi-segment bead–spring chain models with appropriate molecular parameters and have demonstrated that a hi-fidelity multiscale simulation is not only capable of accurately describing the drag on the sphere as a function of 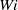at various sphere-to-tube diameter ratios but also it can closely reproduce the experimentally observed velocity and stresses in the wake of the sphere.

JFM classification

Mathematical Foundations: Computational methods Non-Newtonian Flows: Viscoelasticity
Type
Papers
Information
Journal of Fluid Mechanics , Volume 694 , 10 March 2012 , pp. 78 - 99
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abedijaberi, A. & Khomami, B. 2011 On the limitations of elastic dumbbell based constitutive equations in simulation of flow of dilute polymeric solutions with stagnation points. J. Non-Newtonian Fluid Mech. 166, 533–545.CrossRefGoogle Scholar
2. Abedijaberi, A., Soulages, J., Kroger, M. & Khomami, B. 2008 Flow of branched polymer melts in a lubricated cross-slot channel: a combined computational and experimental study. Rheol. Acta 48, 97–108.CrossRefGoogle Scholar
3. Arigo, M. T., Rajagopalan, D. R., Shapely, N. T. & McKinley, G. H. 1995 The sedimentation of a sphere through an elastic fluid. Part I. Steady motion. J. Non-Newtonian Fluid Mech. 60, 225–257.CrossRefGoogle Scholar
4. Baaijens, F. P. T., Baaijens, H. P. W., Peters, G. W. M. & Meijer, H. E. H. 1994 An exprimental and numerical investigation of a viscoelastic flow around a cylinder. J. Rheol. 38, 351–376.CrossRefGoogle Scholar
5. Baaijens, H. P. W., Peters, G. W. M., baaijens, F. P. T. & Meijer, H. E. H. 1995 Viscoelastic flow past a confined cylinder of a polyisobutylene solution. J. Rheol. 39, 1243–1277.CrossRefGoogle Scholar
6. Bird, R. B., Curtiss, C. F., Armstrong, R. C. & Hassager, O. 1987 Dynamics of Polymeric Liquids, Vol. 2. Wiley.Google Scholar
7. Brooks, A. N. & Hughes, T. J. R. 1982 Streamline Upwind/Petrov–Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier–Stokes equations. Comput. Meth. Appl. Mech. Engng 32, 199–259.CrossRefGoogle Scholar
8. Burghardt, W. R., Li, J., Yang, B. & Khomami, B. 1999 Uniaxial extensional characterization of a shear thinning fluid using axisymmetric flow birefringence. J. Rheol. 43, 147–165.CrossRefGoogle Scholar
9. Doyle, P. S., Shaqfeh, E. S. G. & Spiegelberg, G. H. 1998 Relaxation of dilute polymeric solutions following extensional flow. J. Non-Newtonian Fluid Mech. 76, 79–110.CrossRefGoogle Scholar
10. Gigras, P. G. & Khomami, B. 2002 Adaptive configuration fields: a new multiscale simulation technique for reptation-based models with a stochastic strain measure and local variations of life span distribution. J. Non-Newtonian Fluid Mech. 108, 99–122.CrossRefGoogle Scholar
11. Grillet, A. M., Yang, B. & Khomami, B. 1999 Modelling of viscoelastic lid driven cavity flow using finite element simulations. J. Non-Newtonian Fluid Mech. 88, 99–131.CrossRefGoogle Scholar
12. Guenette, R. & Fortin, M. 1995 A new mixed finite element method for computing viscoelastic flows. J. Non-Newtonian Fluid Mech. 60, 27–52.CrossRefGoogle Scholar
13. Halin, P., Lielens, G., Keunings, R. & Legat, V. 1998 The Lagrangian particle method for macroscopic and micro–macro viscoelastic flow computations. J. Non-Newtonian Fluid Mech. 77, 153–190.Google Scholar
14. Happel, J. & Brenner, H. 1973 Low Reynolds Number Hydrodynamics. Martinus Nijhoff.Google Scholar
15. Harlen, O. G., Rallison, J. M. & Chilcott, M. D. 1990 High-Deborah-number flow of a dilute polymer solution past a sphere falling along the axis of a cylindrical tube. J. Non-Newtonian Fluid Mech. 33, 157–173.CrossRefGoogle Scholar
16. Hulsen, M. A., van Heel, A. P. G. & van den Brule, B. H. A. A. 1997 Simulation of viscoelastic flows usign Brownian configuration fields. J. Non-Newtonian Fluid Mech. 70, 79–101.CrossRefGoogle Scholar
17. Khomami, B., Talwar, K. K. & Ganpule, H. K. 1994 A comparative study of higher and lower order finite element techniques for computation of viscoelastic flows. J. Rheol. 38, 255–289.CrossRefGoogle Scholar
18. Koppol, A. P., Sureshkumar, R., Abedijaberi, A. & Khomami, B. 2009 Anomalous pressure drop behaviour of mixed kinematics flows of viscoelastic polymer solutions: a multiscale simulation approach. J. Fluid Mech. 631, 231–253.CrossRefGoogle Scholar
19. Koppol, A. P., Sureshkumar, R. & Khomami, B. 2007 An efficient algorithm for multiscale flow simulation of dilute polymeric solutions using bead-spring chains. J. Non-Newtonian Fluid Mech. 141, 180–192.CrossRefGoogle Scholar
20. Larson, R. 2005 The rheology of dilute solutions of flexible polymers: progress and problems. J. Rheol. 49, 1–70.CrossRefGoogle Scholar
21. Laso, M. & Öttinger, H. C. 1993 Calculation of viscoelastic flow using molecular models: the CONNFFESSIT approach. J. Non-Newtonian Fluid Mech. 47, 1–20.CrossRefGoogle Scholar
22. Li, J., Burghardt, W. R., Yang, B. & Khomami, B. 1998 Flow birefringence and computational studies of a shear thinning polymer solution in axisymmetric stagnation flow. J. Non-Newtonian Fluid Mech. 74, 151–193.CrossRefGoogle Scholar
23. Li, J., Burghardt, W. R., Yang, B. & Khomami, B. 2000 Birefringence and computational studies of a polystyrene Boger fluid in axisymmetric stagnation flow. J. Non-Newtonian Fluid Mech. 91, 189–220.CrossRefGoogle Scholar
24. Lunsmann, W. J., Geniser, L., Brown, R. A. & Armstrong, R. C. 1993 Finite element analysis of steady viscoelastic flow around a sphere: calculations with constant viscosity models. J. Non-Newtonian Fluid Mech. 48, 63–99.CrossRefGoogle Scholar
25. McKinley, G. H. 2001 Transport Processes in Bubbles, Drops and Particles. Taylor & Francis.Google Scholar
26. McKinley, G. H., Armstrong, R. C. & Brown, R. A. 1993 The wake instability in viscoelastic flow past confined circular cylinders. Phil. Trans. R. Soc. Lond. A 344, 265–304.Google Scholar
27. Öttinger, H. C., van den Brule, B. H. A. A. & Hulsen, M. A. 1997 Brownian configuration fields and variance reduce CONNFFESSIT. J. Non-Newtonian Fluid Mech. 70, 255–261.CrossRefGoogle Scholar
28. Perkins, T. T., Smith, D. E. & Chu, S. 1997 Single polymer dynamics in an elongational flow. Science 276, 2016–2021.CrossRefGoogle Scholar
29. Quinzani, L. M., Armstrong, R. C. & Brown, R. A. 1994 Birefringence and laser-doppler velocimetry (LDV) studies of viscoelastic flow through a planar contraction. J. Non-Newtonian Fluid Mech. 52, 1–36.CrossRefGoogle Scholar
30. Rasmussen, H. K. & Hassager, O. 1996 On the sedimentation velocity of spheres in a polymeric liquid. Chem. Engng Sci. 51, 1431–1440.CrossRefGoogle Scholar
31. Rothstein, J. P. & McKinley, G. H. 1999 Extensional flow of a polystyrene Boger fluid through a 4:1:4 contraction/expansion. J. Non-Newtonian Fluid Mech. 86, 61–88.CrossRefGoogle Scholar
32. Rothstein, J. P. & McKinley, G. H. 2001 The axisymmetric contraction–expansion: the role of extensional rheology on vortex growth dynamics and the enhanced pressure drop. J. Non-Newtonian Fluid Mech. 98, 33–63.CrossRefGoogle Scholar
33. Satrape, J. V. & Crochet, M. J. 1994 Numerical simulation of the motion of a sphere in a Boger fluid. J. Non-Newtonian Fluid Mech. 55, 91–111.CrossRefGoogle Scholar
34. Shaqfeh, E. S. G. 2005 The dynamics of single-molecule DNA in flow. J. Non-Newtonian Fluid Mech. 130, 1–28.CrossRefGoogle Scholar
35. Somasi, M. 2001 Dynamics of polymeric fluids, a combined Brownian dynamics finite element approach. PhD Thesis, Washington University in St Louis.Google Scholar
36. Somasi, M. & Khomami, B. 2000 Linear stability and dynamics of viscoelastic flows using time-dependent stochastic simulation techniques. J. Non-Newtonian Fluid Mech. 93, 339–362.CrossRefGoogle Scholar
37. Somasi, M. & Khomami, B. 2001 A new approach for studying the hydrodynamic stability of fluids with microstructure. Phys. Fluids 13, 1811–1814.CrossRefGoogle Scholar
38. Somasi, M., Khomami, B., Woo, N. J., Hur, J. S. & Shaqfeh, J. S. 2002 Brownian dynamics simulations of bead-rod and bead-spring chains: numerical algorithms and coarse-graining issues. J. Non-Newtonian Fluid Mech. 108, 227–255.CrossRefGoogle Scholar
39. Szabó, B. & Babus˜ka, Ivo 1987 Finite Element Analysis. John Wiley and Sons Inc.Google Scholar
40. Szady, M. J., Salamon, T., Liu, A. W., Bornside, D. E, Armstrong, R. C. & Brown, R. A. 1995 A new mixed finite element method for viscoelastic flows governed by differential constitutive equations. J. Non-Newtonian Fluid Mech. 59, 215–243.CrossRefGoogle Scholar
41. Talwar, K. K., Ganpule, H. K. & Khomami, B. 1994 A note on the selection of spaces in computation of viscoelastic flows using the hp-finite element method. J. Non-Newtonian Fluid Mech. 52, 293–307.CrossRefGoogle Scholar
42. Talwar, K. K. & Khomami, B. 1992 Application of higher order finite element methods to viscoelastic flow in porous media. J. Rheol. 36, 1377–1416.CrossRefGoogle Scholar
43. Talwar, K. K. & Khomami, B. 1995 Flow of viscoelastic fluids past periodic square arrays of cylinders: inertial and shear thinning viscosity and elasticity effects. J. Non-Newtonian Fluid Mech. 57, 197–202.CrossRefGoogle Scholar
44. Thomas, D. G., DePuit, R. J. & Khomami, B. 2009 Simulations of single DNA molecules in oscillatory shear flow. J. Rheol. 53, 275.CrossRefGoogle Scholar
45. Venkataramani, V., Sureshkumar, R. & Khomami, B. 2008a Coarse-grained modelling of macromolecular solutions using a configuration-based approach. J. Rheol. 52, 1143.CrossRefGoogle Scholar
46. Venkataramani, V., Sureshkumar, R. & Khomami, B. 2008b A computationally efficient approach for Hi fidelity fine graining from bead-spring models to bead-rod models. J. Non-Newtonian Fluid Mech. 149, 20–27.CrossRefGoogle Scholar
47. Verhoef, M. R. J., van den Brule, B. H. A. A. & Hulsen, M. A. 1999 On the modelling of a PIB/PB Boger fluid in extensional flow. J. Non-Newtonian Fluid Mech. 80, 155–182.CrossRefGoogle Scholar
48. Wapperom, P., Keunings, R. & Legat, V. 2000 The backward-tracking Lagrangian particle method for transient viscoelastic flows. J. Non-Newtonian Fluid Mech. 91, 273–295.CrossRefGoogle Scholar
49. Wiest, J. M. & Tanner, R. I. 1989 Rheology of bead-nonlinear spring chain macromolecules. J. Rheol. 33, 281–316.CrossRefGoogle Scholar
50. Yang, B. & Khomami, B. 1999 Simulation of sedimentation of a sphere in a viscoelastic fluid using molecular based constitutive models. J. Non-Newtonian Fluid Mech. 82, 429–452.CrossRefGoogle Scholar