Article contents
Secondary instability analysis of crossflow on a hypersonic yawed straight circular cone
Published online by Cambridge University Press: 28 December 2016
Abstract
The purpose of this paper is to provide secondary instability analysis of stationary crossflow vortices on a hypersonic yawed straight circular cone with a 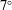 $7^{\circ }$ half-angle at
$7^{\circ }$ half-angle at 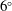 $6^{\circ }$ angle of attack, free-stream Mach number 6 and unit Reynolds number
$6^{\circ }$ angle of attack, free-stream Mach number 6 and unit Reynolds number 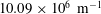 $10.09\times 10^{6}~\text{m}^{-1}$. At an angle of attack, a three-dimensional boundary layer is developed between the windward and leeward symmetry planes. Under the action of azimuthal pressure gradients, the flow near the surface is deflected more than the flow near the edge of the boundary layer. This results in an inflectional velocity profile that can sustain the growth of crossflow vortices. The stationary crossflow instability is computed by means of the nonlinear parabolized stability equations, including a methodology to predict the stationary-crossflow marching path and variation of the spanwise number of waves in the marching direction solely from the basic state. Secondary instability analysis is performed using spatial BiGlobal equations based on two-dimensional partial differential equations. The secondary instabilities are calculated at different axial locations along two crossflow vortex trajectories selected to complement experiments conducted in the Mach 6 Quiet Tunnel at Texas A&M University and in the Boeing/AFOSR Mach 6 Quiet Tunnel at Purdue University. The secondary instability analysis captures various instability modes. Similar to observations in the low-speed regime for an infinite swept wing, secondary shear-layer instabilities are amplified as a consequence of the three-dimensional shear layer formed by crossflow vortices. Also, low-frequency travelling crossflow and high-frequency second modes coexist with the shear-layer instabilities. These results are shown to be in good agreement with the two sets of hypersonic yawed cone experiments (one with natural surface roughness and one with artificial discrete roughness) and compare well with experimental measurements of an incompressible swept wing.
$10.09\times 10^{6}~\text{m}^{-1}$. At an angle of attack, a three-dimensional boundary layer is developed between the windward and leeward symmetry planes. Under the action of azimuthal pressure gradients, the flow near the surface is deflected more than the flow near the edge of the boundary layer. This results in an inflectional velocity profile that can sustain the growth of crossflow vortices. The stationary crossflow instability is computed by means of the nonlinear parabolized stability equations, including a methodology to predict the stationary-crossflow marching path and variation of the spanwise number of waves in the marching direction solely from the basic state. Secondary instability analysis is performed using spatial BiGlobal equations based on two-dimensional partial differential equations. The secondary instabilities are calculated at different axial locations along two crossflow vortex trajectories selected to complement experiments conducted in the Mach 6 Quiet Tunnel at Texas A&M University and in the Boeing/AFOSR Mach 6 Quiet Tunnel at Purdue University. The secondary instability analysis captures various instability modes. Similar to observations in the low-speed regime for an infinite swept wing, secondary shear-layer instabilities are amplified as a consequence of the three-dimensional shear layer formed by crossflow vortices. Also, low-frequency travelling crossflow and high-frequency second modes coexist with the shear-layer instabilities. These results are shown to be in good agreement with the two sets of hypersonic yawed cone experiments (one with natural surface roughness and one with artificial discrete roughness) and compare well with experimental measurements of an incompressible swept wing.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 59
- Cited by



