Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-24T22:51:25.772Z Has data issue: false hasContentIssue false
  • English
  • Français

Scaling of the turbulent/non-turbulent interface in boundary layers

Published online by Cambridge University Press:  19 June 2014

Kapil Chauhan ,
Jimmy Philip  and
Ivan Marusic
Kapil Chauhan*
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Parkville, VIC 3010, Australia
Jimmy Philip
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Parkville, VIC 3010, Australia
Ivan Marusic
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Parkville, VIC 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

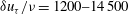Scaling of the interface that demarcates a turbulent boundary layer from the non-turbulent free stream is sought using theoretical reasoning and experimental evidence in a zero-pressure-gradient boundary layer. The data-analysis, utilising particle image velocimetry (PIV) measurements at four different Reynolds numbers ($\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\delta u_{\tau }/\nu =1200\mbox{--}14\, 500$), indicates the presence of a viscosity dominated interface at all Reynolds numbers. It is found that the mean normal velocity across the interface and the tangential velocity jump scale with the skin-friction velocity 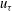$u_{\tau }$ and are approximately 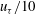$u_{\tau }/10$ and 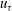$u_{\tau }$, respectively. The width of the superlayer is characterised by the local vorticity thickness 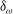$\delta _{\omega }$ and scales with the viscous length scale 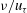$\nu /u_{\tau }$. An order of magnitude analysis of the tangential momentum balance within the superlayer suggests that the turbulent motions also scale with inner velocity and length scales 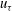$u_{\tau }$ and 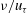$\nu /u_{\tau }$, respectively. The influence of the wall on the dynamics in the superlayer is considered via Townsend’s similarity hypothesis, which can be extended to account for the viscous influence at the turbulent/non-turbulent interface. Similar to a turbulent far-wake the turbulent motions in the superlayer are of the same order as the mean velocity deficit, which lends to a physical explanation for the emergence of the wake profile in the outer part of the boundary layer.

JFM classification

Boundary Layers: Boundary Layers Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 751 , 25 July 2014 , pp. 298 - 328
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.CrossRefGoogle Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Anand, R., Boersma, B. J. & Agrawal, A. 2009 Detection of turbulent/non-turbulent interface for an axisymmetric turbulent jet: evaluation of known criteria and proposal of a new criterion. Exp. Fluids 47 (6), 995–1007.CrossRefGoogle Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2014 Velocity statistics in turbulent channel flow up to $Re_{\tau }=4000$ . J. Fluid Mech. 742, 171–191.CrossRefGoogle Scholar
Bisset, D. K., Hunt, J. C. R. & Rogers, M. M. 2002 The turbulent/non-turbulent interface bounding a far wake. J. Fluid Mech. 451, 383–410.CrossRefGoogle Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64, 775–816.CrossRefGoogle Scholar
Chauhan, K. A., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41, 021404.CrossRefGoogle Scholar
Chauhan, K., Philip, J., de Silva, C., Hutchins, N. & Marusic, I. 2014 The turbulent/non-turbulent interface and entrainment in a boundary layer. J. Fluid Mech. 742, 119–151.CrossRefGoogle Scholar
Christensen, K. T. 2004 The influence of peak-locking errors on turbulence statistics computed from PIV ensembles. Exp. Fluids 36 (3), 484–497.CrossRefGoogle Scholar
Coles, D. E. & Hirst, E. A.1968 Computation of turbulent boundary layers. In Proceedings of AFOSR-IFP Stanford Conference, Stanford, CA, vol. 2.Google Scholar
Corrsin, S. & Kistler, A. L.1955 Free-stream boundaries of turbulent flows. NACA Tech. Rep. TN-1244, Washington, DC.Google Scholar
Dimotakis, P. E. 2005 Turbulent mixing. Annu. Rev. Fluid Mech. 37, 329–356.CrossRefGoogle Scholar
Falco, R. E. 1977 Coherent motions in the outer region of turbulent boundary layers. Phys. Fluids Suppl. 20, S132.Google Scholar
Hambleton, W., Hutchins, N. & Marusic, I. 2005 Simultaneous orthogonal plane PIV measurements in a turbulent boundary layer. J. Fluid Mech. 560, 53–64.CrossRefGoogle Scholar
Head, M. R. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–338.CrossRefGoogle Scholar
Herpin, S., Stanislas, M., Foucaut, J. M. & Coudert, S. 2013 Influence of the Reynolds number on the vortical structures in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 716, 5–50.CrossRefGoogle Scholar
Holzner, M., Liberzon, A., Nikitin, N., Kinzelbach, W. & Tsinober, A. 2007 Small-scale aspects of flows in proximity of the turbulent/nonturbulent interface. Phys. Fluids 19, 071702.CrossRefGoogle Scholar
Holzner, M., Liberzon, A., Nikitin, N., Lüthi, B., Kinzelbach, W. & Tsinober, A. 2008 A Lagrangian investigation of the small-scale features of turbulent entrainment through particle tracking and direct numerical simulation. J. Fluid Mech. 598, 465–475.CrossRefGoogle Scholar
Holzner, M. & Lüthi, B. 2011 Laminar superlayer at the turbulence boundary. Phys. Rev. Lett. 106, 134503.CrossRefGoogle ScholarPubMed
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to $\mathit{Re} = 2003$ . Phys. Fluids 18, 011702.CrossRefGoogle Scholar
Huffman, D. G. & Bradshaw, P. 1972 A note on von Kármán’s constant in low Reynolds number turbulent flows. J. Fluid Mech. 53 (1), 45–60.CrossRefGoogle Scholar
Hunt, J. C. R., Rottman, J. W. & Britter, R. E. 1984 Some physical processes involved in the dispersion of dense gases. In Proceedings of IUTAM Symposium ‘Atmospheric Dispersion of Heavy Gases and Small Particles’ (ed. Ooms, G. & Tennekes, H.), pp. 361–395. Springer.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.CrossRefGoogle Scholar
Jiménez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611, 215–236.CrossRefGoogle Scholar
Kovasznay, L. S. G. 1967 Structure of the turbulent boundary layer. Phys. Fluids Suppl. 10, S25–S30.CrossRefGoogle Scholar
Kulandaivelu, V.2012 Evolution of zero pressure gradient turbulent boundary layers from different initial conditions. PhD thesis, The University of Melbourne, Melbourne, Australia.Google Scholar
Marusic, I. & Adrian, R. J. 2012 The eddies and scales of wall turbulence. In Ten Chapters in Turbulence (ed. Kaneda, Y., Sreenivasan, K. R. & Davidson, P. A.), pp. 176–220. Cambridge University Press.CrossRefGoogle Scholar
Marusic, I., Uddin, A. K. M. & Perry, A. E. 1997 Similarity law for the streamwise turbulence intensity in zero-pressure-gradient turbulent boundary layers. Phys. Fluids 9, 3718–3726.CrossRefGoogle Scholar
Meinhart, C. D. & Adrian, R. J. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phys. Fluids 7, 694–696.CrossRefGoogle Scholar
Monkewitz, P. A., Chauhan, K. A. & Nagib, H. M. 2007 Self-consistent high-Reynolds-number asymptotics for zero-pressure-gradient turbulent boundary layers. Phys. Fluids 19, 115101.CrossRefGoogle Scholar
Monkewitz, P. A., Chauhan, K. A. & Nagib, H. M. 2008 Comparison of mean flow similarity laws in zero pressure gradient turbulent boundary layers. Phys. Fluids 20, 105102.CrossRefGoogle Scholar
Morrill-Winter, C. & Klewicki, J. 2013 Influences of boundary layer scale separation on the vorticity transport contribution to turbulent inertia. Phys. Fluids 25, 015108.CrossRefGoogle Scholar
Morton, B. R., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Phil. Trans. R. Soc. Lond. A 234 (1196), 1–23.Google Scholar
Murlis, J., Tsai, H. M. & Bradshaw, P. 1982 The structure of turbulent boundary layers at low Reynolds numbers. J. Fluid Mech. 122 (1), 13–56.CrossRefGoogle Scholar
Nagib, H. M. & Chauhan, K. A. 2008 Variations of von Kármán coefficient in canonical flows. Phys. Fluids 20, 101518.CrossRefGoogle Scholar
Nee, V. W. & Kovasznay, L. S. G. 1969 Simple phenomenological theory of turbulent shear flows. Phys. Fluids 12, 473.CrossRefGoogle Scholar
Paizis, S. T. & Schwarz, W. H. 1974 An investigation of the topography and motion of the turbulent interface. J. Fluid Mech. 63 (2), 315–343.CrossRefGoogle Scholar
Philip, J. & Marusic, I. 2012 Large-scale eddies and their role in entrainment in turbulent jets and wakes. Phys. Fluids 24, 055108.CrossRefGoogle Scholar
Philip, J., Meneveau, C., de Silva, C. M. & Marusic, I. 2014 Multiscale analysis of fluxes at the turbulent/non-turbulent interface in high Reynolds number boundary layers. Phys. Fluids 26 (1), 015105.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Reynolds, W. C. 1972 Large-scale instabilities of turbulent wakes. J. Fluid Mech. 54, 481–488.CrossRefGoogle Scholar
Schultz, M. P. & Flack, K. A. 2007 The rough-wall turbulent boundary layer from the hydraulically smooth to the fully rough regime. J. Fluid Mech. 580, 381–405.CrossRefGoogle Scholar
da Silva, C. B. & dos Reis, R. J. N. 2011 The role of coherent vortices near the turbulent/non-turbulent interface in a planar jet. Phil. Trans. R. Soc. Lond. A 369, 738–753.Google Scholar
da Silva, C. B., Hunt, J. C. R., Eames, I. & Westerweel, J. 2014 Interfacial layers between regions of different turbulence intensity. Annu. Rev. Fluid Mech. 46 (1), 567–590.CrossRefGoogle Scholar
da Silva, C. B. & Pereira, J. C. F. 2008 Invariants of the velocity-gradient, rate-of-strain, and rate-of-rotation tensors across the turbulent/nonturbulent interface in jets. Phys. Fluids 20 (5), 055101.CrossRefGoogle Scholar
da Silva, C. B. & Taveira, R. R. 2010 The thickness of the turbulent/nonturbulent interface is equal to the radius of the large vorticity structures near the edge of the shear layer. Phys. Fluids 22, 121702.CrossRefGoogle Scholar
da Silva, C. B. & Taveira, R. R.2013 The turbulent/non-turbulent interface and viscous superlayer in turbulent planar jets. In Proceedings of 14th European Turbulence Conference, 1–4 September, Lyon, France.CrossRefGoogle Scholar
de Silva, C. M., Chauhan, K. A., Atkinson, C. H., Buchmann, N. A., Hutchins, N., Soria, J. & Marusic, I.2012 Implementation of large scale PIV measurements for wall bounded turbulence at high Reynolds numbers. In Proceedings of 18th Australasian Fluid Mechanics Conference, 3–7 December, Launceston, Australia.Google Scholar
de Silva, C. M., Gnanamanickam, E. P., Atkinson, C., Buchmann, N. A., Hutchins, N., Soria, J. & Marusic, I. 2014 High spatial range velocity measurements in a high Reynolds number turbulent boundary layer. Phys. Fluids 26 (2), 025117.CrossRefGoogle Scholar
de Silva, C. M., Philip, J., Chauhan, K., Meneveau, C. & Marusic, I. 2013 Multiscale geometry and scaling of the turbulent-nonturbulent interface in high Reynolds number boundary layers. Phys. Rev. Lett. 111, 044501.CrossRefGoogle ScholarPubMed
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.CrossRefGoogle Scholar
Sreenivasan, K. R., Prasad, R. R., Meneveau, C. & Ramshankar, R. 1989a The fractal geometry of interfaces and the multifractal distribution of dissipation in fully turbulent flows. Pure Appl. Geophys. 131 (1), 43–60.CrossRefGoogle Scholar
Sreenivasan, K. R., Ramshankar, R. & Meneveau, C. 1989b Mixing, entrainment and fractal dimensions of surfaces in turbulent flows. Phil. Trans. R. Soc. Lond. A 421 (1860), 79–108.Google Scholar
Taveira, R. R. & da Silva, C. B. 2013 Kinetic energy budgets near the turbulent/nonturbulent interface in jets. Phys. Fluids 25, 015114.CrossRefGoogle Scholar
Taylor, G. I. 1938 Production and dissipation of vorticity in a turbulent fluid. Phil. Trans. R. Soc. Lond. A 164 (916), 15–23.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. The MIT Press.CrossRefGoogle Scholar
Townsend, A. A. 1956 The Structure of Turbulent Shear Flow, 1st edn. Cambridge University Press.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Turner, J. S. 1986 Turbulent entrainment: the development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech. 173, 431–471.CrossRefGoogle Scholar
Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2005 Mechanics of the turbulent-nonturbulent interface of a jet. Phys. Rev. Lett. 95, 174501.Google ScholarPubMed
Wolf, M., Holzner, M., Lüthi, B., Krug, D., Kinzelbach, W. & Tsinober, A. 2013 Effects of mean shear on the local turbulent entrainment process. J. Fluid Mech. 731, 95–116.CrossRefGoogle Scholar
Wolf, M., Lüthi, B., Holzner, M., Krug, D., Kinzelbach, W. & Tsinober, A. 2012 Investigations on the local entrainment velocity in a turbulent jet. Phys. Fluids 24, 105110.CrossRefGoogle Scholar
Wu, Y. & Christensen, K. T. 2007 Outer-layer similarity in the presence of a practical rough-wall topography. Phys. Fluids 19, 085108.CrossRefGoogle Scholar