Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T19:38:44.952Z Has data issue: false hasContentIssue false
  • English
  • Français

The scaling of the turbulent/non-turbulent interface at high Reynolds numbers

Published online by Cambridge University Press:  21 March 2018

Tiago S. Silva ,
Marco Zecchetto  and
Carlos B. da Silva Open the ORCID record for Carlos B. da Silva [Opens in a new window]
Tiago S. Silva
Affiliation:
LAETA, IDMEC, Instituto Superior Técnico, Universidade de Lisboa, Avenida Rovisco Pais 1, 1049-001 Lisboa, Portugal
Marco Zecchetto
Affiliation:
LAETA, IDMEC, Instituto Superior Técnico, Universidade de Lisboa, Avenida Rovisco Pais 1, 1049-001 Lisboa, Portugal
Carlos B. da Silva*
Affiliation:
LAETA, IDMEC, Instituto Superior Técnico, Universidade de Lisboa, Avenida Rovisco Pais 1, 1049-001 Lisboa, Portugal
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

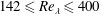The scaling of the turbulent/non-turbulent interface (TNTI) at high Reynolds numbers is investigated by using direct numerical simulations (DNS) of temporal turbulent planar jets (PJET) and shear free turbulence (SFT), with Reynolds numbers in the range $142\leqslant Re_{\unicode[STIX]{x1D706}}\leqslant 400$. For 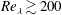$Re_{\unicode[STIX]{x1D706}}\gtrsim 200$ the thickness of the TNTI (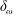$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}$), like that of its two sublayers – the viscous superlayer (VSL, 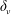$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$) and the turbulent sublayer (TSL, 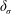$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}}$) – all scale with the Kolmogorov micro-scale 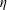$\unicode[STIX]{x1D702}$, while the particular scaling constant depends on the sublayer. Specifically, for 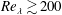$Re_{\unicode[STIX]{x1D706}}\gtrsim 200$ while the VSL is always of the order of 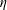$\unicode[STIX]{x1D702}$, with 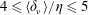$4\leqslant \langle \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}\rangle /\unicode[STIX]{x1D702}\leqslant 5$, the TSL and the TNTI are typically equal to 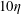$10\unicode[STIX]{x1D702}$, with 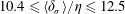$10.4\leqslant \langle \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}}\rangle /\unicode[STIX]{x1D702}\leqslant 12.5$, and 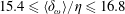$15.4\leqslant \langle \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}\rangle /\unicode[STIX]{x1D702}\leqslant 16.8$, respectively.

JFM classification

Wakes/Jets: Jets Turbulent Flows: Shear layer turbulence Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 843 , 25 May 2018 , pp. 156 - 179
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alvelius, K. 1999 Random forcing of three-dimensional homogeneous turbulence. Phys. Fluids 11 (7), 1880–1889.Google Scholar
Attili, A., Cristancho, J. C. & Bisetti, F. 2014 Statistics of the turbulent/non-turbulent interface in a spatially developing mixing layer. J. Turbul. 15, 555–568.Google Scholar
Bisset, D. K., Hunt, J. C. R. & Rogers, M. M. 2002 The turbulent/non-turbulent interface bounding a far wake. J. Fluid Mech. 451, 383–410.Google Scholar
Borrell, G. & Jiménez, J. 2016 Properties of the turbulent/non-turbulent interface in boundary layers. J. Fluid Mech. 801, 554–596.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 1987 Spectral Methods in Fluid Dynamics. Springer.Google Scholar
Carruthers, D. J. & Hunt, J. C. R. 1986 Velocity fluctuations near an interface between a turbulent region and a stably stratified layer. J. Fluid Mech. 165, 475–501.Google Scholar
Chauhan, K., Philip, J. & Marusic, I. 2014 Scaling of the turbulent/non-turbulent interface in boundary layers. J. Fluid Mech. 751, 1–31.Google Scholar
Cimarelli, A., Cocconi, G., Frohnapfel, B. & Angelis, E. D. 2015 Spectral enstrophy budget in a shear-less flow with turbulent/non-turbulent interface. Phys. Fluids 27, 125106.Google Scholar
Corrsin, S. & Kistler, A. L.1955 Free-stream boundaries of turbulent flows. NACA Tech. Rep. TN-1244.Google Scholar
Elsinga, G., Ishihara, T., Goudar, M. V., da Silva, C. B. & Hunt, J. C. R. 2017 The scaling of straining motions in homogeneous isotropic turbulence. J. Fluid Mech. 829, 31–64.Google Scholar
Gampert, M., Narayanaswamy, V., Schaefer, P. & Peters, N. 2013 Conditional statistics of the turbulent/non-turbulent interface in a jet flow. J. Fluid Mech. 731, 615–638.Google Scholar
Holzner, M., Liberzon, A., Luthi, B., Nikitin, N., Kinzelbach, W. & Tsinober, A. 2008 A Lagrangian investigation of the small-scale features of turbulent entrainment through particle tracking and direct numerical simulation. J. Fluid Mech. 598, 465–475.Google Scholar
Holzner, M., Liberzon, A., Nikitin, N., Kinzelbach, W. & Tsinober, A. 2007 Small-scale aspects of flows in proximity of the turbulent/nonturbulent interface. Phys. Fluids 19, 071702.Google Scholar
Hunt, J. C. R., Eames, I., Westerweel, J., Davidson, P. A., Voropayev, S., Fernando, J. & Braza, M. 2010 Thin shear layers: the key to turbulence structure. J. Hydro-environment Res. 4, 75–82.Google Scholar
Ishihara, T., Kaneda, Y. & Hunt, J. C. R. 2013 Thin shear layers in high Reynolds number turbulence—DNS results. Flow Turbul. Combust. 91, 895–929.Google Scholar
Ishihara, T., Ogasawara, H. & Hunt, J. C. R. 2015 Analysis of conditional statistics obtained near the turbulent/non-turbulent interface of turbulent boundary layers. J. Fluids Struct. 53, 50–57.Google Scholar
Jiménez, J. & Wray, A. 1998 On the characteristics of vortex filaments in isotropic turbulence. J. Fluid Mech. 373, 255–285.Google Scholar
Khashehchi, M. & Marusic, I. 2013 Evolution of the turbulent/non-turbulent interface of an axisymmetric turbulent jet. Exp. Fluids 54, 1449.Google Scholar
Martín, J., Ooi, A., Chong, S. & Soria, J. 1998 Dynamics of the velocity gradient tensor invariants in isotropic turbulence. Phys. Fluids 10 (9), 2336–2346.Google Scholar
Mathew, J. & Basu, A. 2002 Some characteristics of entrainment at a cylindrical turbulent boundary. Phys. Fluids 14 (7), 2065–2072.Google Scholar
Perot, B. & Moin, P. 1995 Shear-free turbulent boundary layers. Part 1. Physical insights into near-wall turbulence. J. Fluid Mech. 295, 199–227.Google Scholar
van Reeuwijk, M. & Holzner, M. 2014 The turbulence boundary of a temporal jet. J. Fluid Mech. 739, 254–275.Google Scholar
da Silva, C. B., Hunt, J. C. R., Eames, I. & Westerweel, J. 2014a Interfacial layers between regions of different turbulent intensity. Annu. Rev. Fluid Mech. 46, 567–590.Google Scholar
da Silva, C. B. & Pereira, J. C. F. 2008 Invariants of the velocity-gradient, rate-of-strain, and rate-of-rotation tensors across the turbulent/nonturbulent interface in jets. Phys. Fluids 20, 055101.Google Scholar
da Silva, C. B., dos Reis, R. J. N. & Pereira, J. C. F. 2011 The intense vorticity structures near the turbulent/non-turbulent interface in a jet. J. Fluid Mech. 685, 165–190.Google Scholar
da Silva, C. B. & Taveira, R. R. 2010 The thickness of the turbulent/nonturbulent interface is equal to the radius of the large vorticity structures near the edge of the shear layer. Phys. Fluids 22, 121702.Google Scholar
da Silva, C. B., Taveira, R. R. & Borrell, G. 2014b Characteristics of the turbulent–nonturbulent interface in boundary layers, jets and shear free turbulence. J. Phys. 506, 012015.Google Scholar
Stanley, S. & Sarkar, S. 2000 Influence of nozzle conditions and discrete forcing on turbulent planar jets. AIAA J. 38, 1615–1623.Google Scholar
Stanley, S., Sarkar, S. & Mellado, J. P. 2002 A study of the flowfield evolution and mixing in a planar turbulent jet using direct numerical simulation. J. Fluid Mech. 450, 377–407.Google Scholar
Taveira, R. R., Diogo, J. S., Lopes, D. C. & da Silva, C. B. 2013 Lagrangian statistics across the turbulent–nonturbulent interface in a turbulent plane jet. Phys. Rev. E 88, 043001.Google Scholar
Taveira, R. R. & da Silva, C. B. 2014 Characteristics of the viscous superlayer in free shear turbulence and in planar turbulent jets. Phys. Fluids 26, 021702.Google Scholar
Teixeira, M. A. C. & da Silva, C. B. 2012 Turbulence dynamics near a turbulent/non-turbulent interface. J. Fluid Mech. 695, 257–287.Google Scholar
Watanabe, T., Nagata, K. & da Silva, C. B. 2017 Vorticity evolution near the turbulent/non-turbulent interfaces in free-shear flows. In Vortex Structures in Fluid Dynamic Problems (ed. Perez-De-Tejada, H.), pp. 1–18. InTech.Google Scholar
Watanabe, T., Riley, J. J., de Bruyn Kops, S. M., Diamessis, P. J. & Zhou, Q. 2016a Turbulent/non-turbulent interfaces in wakes in stably stratified fluids. J. Fluid Mech. 797, 1–11.Google Scholar
Watanabe, T., Sakai, Y., Nagata, K., Ito, Y. & Hayase, T. 2014 Vortex stretching and compression near the turbulent/non-turbulent interface in a planar jet. J. Fluid Mech. 758, 754–784.Google Scholar
Watanabe, T., Sakai, Y., Nagata, K., Ito, Y. & Hayase, T. 2015 Turbulent mixing of passive scalar near turbulent and non-turbulent interface in mixing layers. Phys. Fluids 27, 085109.Google Scholar
Watanabe, T., da Silva, C. B., Sakai, Y., Nagata, K. & Hayase, T. 2016b Lagrangian properties of the entrainment across turbulent/non-turbulent interface layers. Phys. Fluids 28, 031701.Google Scholar
Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2009 Momentum and scalar transport at the turbulent/non-turbulent interface of a jet. J. Fluid Mech. 631, 199–230.Google Scholar
Williamson, J. H. 1980 Low-storage Runge–Kutta schemes. J. Comput. Phys. 35, 48–56.Google Scholar
Wolf, M., Holzner, M., Luthi, B., Krug, D., Kinzelbach, W. & Tsinober, A. 2013 Effects of mean shear on the local turbulent entrainment process. J. Fluid Mech. 731, 95–116.Google Scholar
Zhou, Y. & Vassilicos, J. C. 2017 Related self-similar statistics of the turbulent/non-turbulent interface and the turbulence dissipation. J. Fluid Mech. 821, 440–457.Google Scholar