Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-28T07:05:15.540Z Has data issue: false hasContentIssue false
  • English
  • Français

Scaling arguments for the fluxes in turbulent miscible fountains

Published online by Cambridge University Press:  11 March 2014

H. C. Burridge  and
G. R. Hunt
H. C. Burridge
Affiliation:
Department of Engineering, University of Cambridge, Cambridge CB2 1PZ, UK
G. R. Hunt*
Affiliation:
Department of Engineering, University of Cambridge, Cambridge CB2 1PZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For established axisymmetric turbulent miscible Boussinesq fountains in quiescent uniform environments, expressions are developed for the fluxes of volume, momentum and buoyancy at the outflow from the fountain: the outflow referring to the counterflow at the horizontal plane of the source. The fluxes are expressed in terms of the fountain source conditions and two dimensionless functions of the source Froude number, 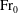${\rm Fr}_{0}$: a radial function (relating a horizontal scale of the outflow to the source radius) and a volume flux function (relating the outflow and source volume fluxes). The forms taken by these two functions at low 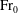${\rm Fr}_{0}$ and high ${\rm Fr}_{0}$ are deduced, thereby providing the outflow fluxes and outflow Froude number solely in terms of the source conditions. For high 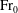${\rm Fr}_{0}$, the outflow Froude number, 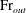${\rm Fr}_{out}$, is shown to be invariant, indicating (by analogy with plumes for which the ‘far-field’ Froude number is invariant with source Froude number) that the outflow may be regarded as ‘far-field’ since the fluxes within the fountain have adjusted to attain a balance which is independent of the source conditions. Based on 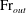${\rm Fr}_{out}$, the fluxes in the plume that forms beyond the fountain outflow are deduced. Finally, from the results of previously published studies, we show that the scalings deduced for fountains are valid for 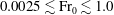$0.0025 \lesssim {\rm Fr}_{0} \lesssim 1.0 $ for low 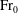${\rm Fr}_{0}$ and 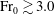$ {\rm Fr}_{0} \gtrsim 3.0 $ for high 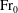${\rm Fr}_{0}$.

JFM classification

Wakes/Jets: Jets Convection: Plumes/thermals Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 744 , 10 April 2014 , pp. 273 - 285
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baines, W. D., Corriveau, A. F. & Reedman, T. J. 1993 Turbulent fountains in a closed chamber. J. Fluid Mech. 255, 621–646.Google Scholar
Baines, W. D., Turner, J. S. & Campbell, I. H. 1990 Turbulent fountains in an open chamber. J. Fluid Mech. 212, 557–592.Google Scholar
Bloomfield, L. J. & Kerr, R. C. 2000 A theoretical model of a turbulent fountain. J. Fluid Mech. 424, 197–216.Google Scholar
Burridge, H. C. & Hunt, G. R. 2012 The rise heights of low- and high-Froude-number turbulent axisymmetric fountains. J. Fluid Mech. 691, 392–416.Google Scholar
Burridge, H. C. & Hunt, G. R. 2013 The rhythm of fountains: the length and time scales of rise height fluctuations at low and high Froude numbers. J. Fluid Mech. 728, 91–119.CrossRefGoogle Scholar
Campbell, I. H. & Turner, J. S. 1989 Fountains in magma chambers. J. Petrol. 30, 885–923.CrossRefGoogle Scholar
Carazzo, G., Kaminski, E. & Tait, S. 2010 The rise and fall of turbulent fountains: a new model for improved quantitative predictions. J. Fluid Mech. 657, 265–284.Google Scholar
Devenish, B. J., Rooney, G. G. & Thompson, D. J. 2010 Large-eddy simulation of a buoyant plume in uniform and stably stratified environments. J. Fluid Mech. 652, 75–103.CrossRefGoogle Scholar
Fischer, H. B., List, E. J., Koh, R. C. Y., Imberger, J. & Brooks, N. H. 1979 Mixing in Inland and Coastal Waters. Academic.Google Scholar
Hunt, G. R. & Kaye, N. G. 2001 Virtual origin correction for lazy turbulent plumes. J. Fluid Mech. 435, 377–396.CrossRefGoogle Scholar
Kaye, N. B. & Hunt, G. R. 2006 Weak fountains. J. Fluid Mech. 558, 319–328.Google Scholar
Lin, W. & Armfield, S. W. 2000 Very weak fountains in a homogeneous fluid. Num. Heat Transfer Part A 38, 377–396.Google Scholar
Lin, Y. J. P. & Linden, P. F. 2005a The entrainment due to a turbulent fountain at a density interface. J. Fluid Mech. 542, 25–52.Google Scholar
Lin, Y. J. P. & Linden, P. F. 2005b A model for an under floor air distribution system. Energy Build. 37 (4), 399–409.Google Scholar
McDougall, T. J. 1981 Negatively buoyant vertical jets. Tellus 33, 313–320.CrossRefGoogle Scholar
Morton, B. R. 1959 Forced plumes. J. Fluid Mech. 5, 151–163.Google Scholar
Morton, B. R. & Middleton, J. 1973 Scale diagrams for forced plumes. J. Fluid Mech. 58, 165–176.Google Scholar
Rajaratnam, N. 1976 Turbulent Jets. Elsevier Science.Google Scholar
Rooney, G. G. & Linden, P. F. 1996 Similarity considerations for non-Boussinesq plumes in an unstratified environment. J. Fluid Mech. 318, 237–250.CrossRefGoogle Scholar
Suzuki, Y. J., Koyaguchi, T., Ogawa, M. & Hachisu, I. 2005 A numerical study of turbulent mixing in eruption clouds using a three-dimensional fluid dynamics model. J. Geophys. Res. 110 (B8).Google Scholar
Turner, J. S. 1966 Jets and plumes with negative or reversing buoyancy. J. Fluid Mech. 26, 779–792.Google Scholar
Van Dyke, M. 1982 An Album of Fluid Motion. Parabolic Press.Google Scholar