Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T21:49:51.522Z Has data issue: false hasContentIssue false
  • English
  • Français

Scaling and dynamics of turbulence over sparse canopies

Published online by Cambridge University Press:  06 February 2020

Akshath Sharma Open the ORCID record for Akshath Sharma [Opens in a new window]  and
Ricardo García-Mayoral Open the ORCID record for Ricardo García-Mayoral [Opens in a new window]
Akshath Sharma
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, CambridgeCB2 1PZ, UK
Ricardo García-Mayoral*
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, CambridgeCB2 1PZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

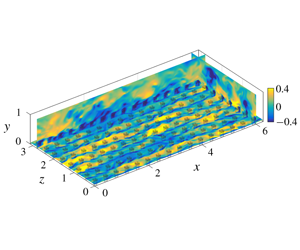
Turbulent flows within and over sparse canopies are investigated using direct numerical simulations at moderate friction Reynolds numbers $Re_{\unicode[STIX]{x1D70F}}\approx 520$ and 1000. The height of the canopies studied is $h^{+}\approx 110{-}200$, which is typical of some engineering canopies but much lower than for most vegetation canopies. The analysis of the effect of Reynolds number in our simulations, however, suggests that the dynamics observed would be relevant for larger Reynolds numbers as well. In channel flows, the distribution of the total stress is linear with height. Over smooth walls, the total stress is the sum of the viscous and the Reynolds shear stresses, the ‘fluid stress’ $\unicode[STIX]{x1D70F}_{f}$. In canopies, in turn, there is an additional contribution from the canopy drag, which can dominate within. Furthermore, the full Reynolds shear stress has contributions from the dispersive, element-induced flow and from the background turbulence, the part of the flow that remains once the element-induced flow is filtered out. For the present sparse canopies, we find that the ratio of the viscous stress and the background Reynolds shear stress to their sum, $\unicode[STIX]{x1D70F}_{f}$, is similar to that over smooth walls at each height, even within the canopy. From this, a height-dependent scaling based on $\unicode[STIX]{x1D70F}_{f}$ is proposed. Using this scaling, the background turbulence within the canopy shows similarities with turbulence over smooth walls. This suggests that the background turbulence scales with $\unicode[STIX]{x1D70F}_{f}$, rather than the conventional scaling based on the total stress. This effect is essentially captured when the canopy is substituted by a drag force that acts on the mean-velocity profile alone, aiming to produce the correct $\unicode[STIX]{x1D70F}_{f}$, without the discrete presence of the canopy elements acting directly on the fluctuations. The proposed mean-only forcing is shown to produce better estimates for the turbulent fluctuations compared to a conventional, homogeneous-drag model. These results suggest that a sparse canopy acts on the background turbulence primarily through the change it induces on the mean-velocity profile, which in turn sets the scale for turbulence, rather than through a direct interaction of the canopy elements with the fluctuations. The effect of the element-induced flow, however, requires the representation of the individual canopy elements.

JFM classification

Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 888 , 10 April 2020 , A1
Copyright
© 2020 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abderrahaman-Elena, N., Fairhall, C. T. & García-Mayoral, R. 2019 Modulation of near-wall turbulence in the transitionally rough regime. J. Fluid Mech. 865, 1042–1071.CrossRefGoogle Scholar
Bai, K., Katz, J. & Meneveau, C. 2015 Turbulent flow structure inside a canopy with complex multi-scale elements. Boundary-Layer Meteorol. 155 (3), 435–457.CrossRefGoogle Scholar
Bailey, B. N. & Stoll, R. 2013 Turbulence in sparse, organized vegetative canopies: a large-eddy simulation study. Boundary-Layer Meteorol. 147 (3), 369–400.CrossRefGoogle Scholar
Bailey, B. N. & Stoll, R. 2016 The creation and evolution of coherent structures in plant canopy flows and their role in turbulent transport. J. Fluid Mech. 789, 425–460.CrossRefGoogle Scholar
Balachandar, S., Mittal, R. & Najjar, F. M. 1997 Properties of the mean recirculation region in the wakes of two-dimensional bluff bodies. J. Fluid Mech. 351, 167–199.CrossRefGoogle Scholar
Bejan, A. & Morega, A. M. 1993 Optimal arrays of pin fins and plate fins in laminar forced convection. Trans. ASME J. Heat Transfer 115 (1), 75–81.CrossRefGoogle Scholar
Belcher, S. E., Harman, I. N. & Finnigan, J. J. 2012 The wind in the willows: flows in forest canopies in complex terrain. Annu. Rev. Fluid Mech. 44, 479–504.CrossRefGoogle Scholar
Böhm, M., Finnigan, J. J., Raupach, M. R. & Hughes, D. 2013 Turbulence structure within and above a canopy of bluff elements. Boundary-Layer Meteorol. 146 (3), 393–419.CrossRefGoogle Scholar
Busse, A. & Sandham, N. D. 2012 Parametric forcing approach to rough-wall turbulent channel flow. J. Fluid Mech. 712, 169–202.CrossRefGoogle Scholar
Cheng, H. & Castro, I. P. 2002 Near wall flow over urban-like roughness. Boundary-Layer Meteorol. 104 (2), 229–259.CrossRefGoogle Scholar
Coceal, O., Thomas, T. & Belcher, S. 2008 Spatially-averaged flow statistics within a canopy of large bluff bodies: results from direct numerical simulations. Acta Geophys. 56 (3), 862–875.CrossRefGoogle Scholar
Coceal, O., Thomas, T. G., Castro, I. P. & Belcher, S. E. 2006 Mean flow and turbulence statistics over groups of urban-like cubical obstacles. Boundary-Layer Meteorol. 121 (3), 491–519.CrossRefGoogle Scholar
Dunn, C., Lopez, F. & Garcia, M. H.1996 Mean flow and turbulence in a laboratory channel with simulated vegatation. Tech. Rep. HES 51. University of Illinois.Google Scholar
Dupont, S. & Brunet, Y. 2008 Influence of foliar density profile on canopy flow: a large-eddy simulation study. Agric. Forest Meteorol. 148 (6–7), 976–990.CrossRefGoogle Scholar
Elahi, H., Eugeni, M. & Gaudenzi, P. 2018 A review on mechanisms for piezoelectric-based energy harvesters. Energies 11 (7), 1850.CrossRefGoogle Scholar
Fairhall, C. T. & García-Mayoral, R. 2018 Spectral analysis of the slip-length model for turbulence over textured superhydrophobic surfaces. Flow Turbul. Combust. 100 (4), 961–978.CrossRefGoogle ScholarPubMed
Fazu, C. & Schwerdtfeger, P. 1989 Flux-gradient relationships for momentum and heat over a rough natural surface. Q. J. R. Meteorol. Soc. 115 (486), 335–352.CrossRefGoogle Scholar
Finnigan, J. J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32 (1), 519–571.CrossRefGoogle Scholar
Finnigan, J. J., Shaw, R. H. & Patton, E. G. 2009 Turbulence structure above a vegetation canopy. J. Fluid Mech. 637, 387–424.CrossRefGoogle Scholar
García-Mayoral, R. & Jiménez, J. 2011 Hydrodynamic stability and breakdown of the viscous regime over riblets. J. Fluid Mech. 678, 317–347.CrossRefGoogle Scholar
Ghisalberti, M. & Nepf, H. M. 2002 Mixing layers and coherent structures in vegetated aquatic flows. J. Geophys. Res. 107 (C2), 3-1–3-11.CrossRefGoogle Scholar
Ghisalberti, M. & Nepf, H. M. 2004 The limited growth of vegetated shear layers. Water Resour. Res. 40 (7), W07502.CrossRefGoogle Scholar
Giometto, M. G., Christen, A., Meneveau, C., Fang, J., Krafczyk, M. & Parlange, M. B. 2016 Spatial characteristics of roughness sublayer mean flow and turbulence over a realistic urban surface. Boundary-Layer Meteorol. 160 (3), 425–452.CrossRefGoogle Scholar
Green, S. R., Grace, J. & Hutchings, N. J. 1995 Observations of turbulent air flow in three stands of widely spaced Sitka spruce. Agric. Forest Meteorol. 74 (3-4), 205–225.CrossRefGoogle Scholar
Högström, U., Bergström, H. & Alexandersson, H. 1982 Turbulence characteristics in a near neutrally stratified urban atmosphere. Boundary-Layer Meteorol. 23 (4), 449–472.CrossRefGoogle Scholar
Huang, J., Cassiani, M. & Albertson, J. D. 2009 The effects of vegetation density on coherent turbulent structures within the canopy sublayer: a large-eddy simulation study. Boundary-Layer Meteorol. 133 (2), 253–275.CrossRefGoogle Scholar
Jackson, P. S. 1981 On the displacement height in the logarithmic velocity profile. J. Fluid Mech. 111, 15–25.CrossRefGoogle Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.CrossRefGoogle Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30 (4), 741–773.CrossRefGoogle Scholar
de Langre, E. 2008 Effects of Wind on Plants. Annu. Rev. Fluid Mech. 40 (1), 141–168.CrossRefGoogle Scholar
Le, H. & Moin, P. 1991 An improvement of fractional step methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 92 (2), 369–379.CrossRefGoogle Scholar
Ledda, P. G., Siconolfi, L., Viola, F., Gallaire, F. & Camarri, S. 2018 Suppression of von Kármán vortex streets past porous rectangular cylinders. Phys. Rev. Fluids 3, 103901.CrossRefGoogle Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 ≈ 5200. J. Fluid Mech. 774, 395–415.CrossRefGoogle Scholar
Lozano-Durán, A. & Bae, H. J. 2019 Characteristic scales of Townsend’s wall-attached eddies. J. Fluid Mech. 868, 698–725.CrossRefGoogle ScholarPubMed
Lozano-Durán, A. & Jiménez, J. 2014 Effect of the computational domain on direct simulations of turbulent channels up to Re 𝜏 = 4200. Phys. Fluids 26 (1), 011702.CrossRefGoogle Scholar
Luhar, M. & Nepf, H. M. 2013 From the blade scale to the reach scale: a characterization of aquatic vegetative drag. Adv. Water Resour. 51, 305–316.CrossRefGoogle Scholar
Luhar, M., Rominger, J. & Nepf, H. 2008 Interaction between flow, transport and vegetation spatial structure. Environ. Fluid Mech. 8 (5-6), 423.CrossRefGoogle Scholar
McCloskey, M. A., Mosher, C. L. & Henderson, E. R. 2017 Wind energy conversion by plant-inspired designs. PLoS One 12 (1), e0170022.CrossRefGoogle ScholarPubMed
McGarry, S. & Knight, C. 2011 The potential for harvesting energy from the movement of trees. Sensors 11 (10), 9275–9299.CrossRefGoogle Scholar
Nepf, H. M. 2012 Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 44 (1), 123–142.CrossRefGoogle Scholar
Nikuradse, J. 1933 Laws of Flow in Rough Pipes. National Advisory Committee for Aeronautics.Google Scholar
Novak, M. D., Warland, J. S., Orchansky, A. L., Ketler, R. & Green, S. 2000 Wind tunnel and field measurements of turbulent flow in forests. Part I: Uniformly thinned stands. Boundary-Layer Meteorol. 95 (3), 457–495.CrossRefGoogle Scholar
Pietri, L., Petroff, A., Amielh, M. & Anselmet, F. 2009 Turbulence characteristics within sparse and dense canopies. Environ. Fluid Mech. 9 (3), 297.CrossRefGoogle Scholar
Poggi, D. & Katul, G. G. 2008 The effect of canopy roughness density on the constitutive components of the dispersive stresses. Exp. Fluids 45 (1), 111–121.CrossRefGoogle Scholar
Poggi, D., Porporato, A., Ridolfi, L., Albertson, J. D. & Katul, G. G. 2004 The effect of vegetation density on canopy sub-layer turbulence. Boundary-Layer Meteorol. 111 (3), 565–587.CrossRefGoogle Scholar
Raupach, M. R., Finnigan, J. J. & Brunet, Y. 1996 Coherent eddies and turbulence in vegetation canopies: the mixing-layer analogy. In Boundary-Layer Meteorology 25th Anniversary Volume, 1970–1995, pp. 351–382. Springer.CrossRefGoogle Scholar
Raupach, M. R., Hughes, D. E. & Cleugh, H. A. 2006 Momentum absorption in rough-wall boundary layers with sparse roughness elements in random and clustered distributions. Boundary-Layer Meteorology 120 (2), 201–218.CrossRefGoogle Scholar
Raupach, M. R. & Shaw, R. H. 1982 Averaging procedures for flow within vegetation canopies. Boundary-Layer Meteorology 22 (1), 79–90.CrossRefGoogle Scholar
Reynolds, W. C. & Hussain, A. K. M. F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54 (2), 263–288.CrossRefGoogle Scholar
Gómez-de Segura, G., Sharma, A. & García-Mayoral, R. 2018 Turbulent drag reduction using anisotropic permeable substrates. Flow Turbul. Combust. 100 (4), 995–1014.CrossRefGoogle ScholarPubMed
Sharma, A. & García-Mayoral, R.2018a Scaling and modelling of turbulent flow over a sparse canopy. arXiv:1810.10028.CrossRefGoogle Scholar
Sharma, A. & García-Mayoral, R. 2018b Turbulent flows over sparse canopies. J. Phys.: Conf. Ser. 1001, 012012.Google Scholar
Sharma, A. & García-Mayoral, R.2019 Turbulent flows over dense filament canopies. arXiv:1907.04020.CrossRefGoogle Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 25 (10), 105102.CrossRefGoogle Scholar
Tanino, Y. & Nepf, H. M. 2008 Laboratory investigation of mean drag in a random array of rigid, emergent cylinders. J. Hydraul. Engng 134 (1), 34–41.CrossRefGoogle Scholar
Taylor, Z. J., Palombi, E., Gurka, R. & Kopp, G. A. 2011 Features of the turbulent flow around symmetric elongated bluff bodies. J. Fluids Struct. 27 (2), 250–265.CrossRefGoogle Scholar
Tuerke, F. & Jiménez, J. 2013 Simulations of turbulent channels with prescribed velocity profiles. J. Fluid Mech. 723, 587–603.CrossRefGoogle Scholar
Yan, C., Huang, W., Miao, S., Cui, G. & Zhang, Z. 2017 Large-eddy simulation of flow over a vegetation-like canopy modelled as arrays of bluff-body elements. Boundary-layer Meteorol. 165 (2), 233–249.CrossRefGoogle Scholar
Yu, P., Zeng, Y., Lee, T. S., Bai, H. X. & Low, H. T. 2010 Wake structure for flow past and through a porous square cylinder. Intl J. Heat Fluid Flow 31 (2), 141–153.CrossRefGoogle Scholar
Yue, W., Parlange, M. B., Meneveau, C., Zhu, W., van Hout, R. & Katz, J. 2007 Large-eddy simulation of plant canopy flows using plant-scale representation. Boundary-Layer Meteorol. 124 (2), 183–203.CrossRefGoogle Scholar
Zampogna, G. A. & Bottaro, A. 2016 Fluid flow over and through a regular bundle of rigid fibres. J. Fluid Mech. 792, 5–35.CrossRefGoogle Scholar
Zhu, W., Van Hout, R., Luznik, L., Kang, H. S., Katz, J. & Meneveau, C. 2006 A comparison of PIV measurements of canopy turbulence performed in the field and in a wind tunnel model. Exp. Fluids 41 (2), 309–318.CrossRefGoogle Scholar