Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-24T17:03:45.688Z Has data issue: false hasContentIssue false
  • English
  • Français

Saturation of a turbulent mixing layer over a cavity: response to harmonic forcing around mean flows

Published online by Cambridge University Press:  23 August 2018

E. Boujo Open the ORCID record for E. Boujo [Opens in a new window] ,
M. Bauerheim  and
N. Noiray
E. Boujo*
Affiliation:
CAPS Lab, Mechanical and Process Engineering Department, ETH Zürich, CH-8092 Zürich, Switzerland
M. Bauerheim
Affiliation:
CAPS Lab, Mechanical and Process Engineering Department, ETH Zürich, CH-8092 Zürich, Switzerland
N. Noiray*
Affiliation:
CAPS Lab, Mechanical and Process Engineering Department, ETH Zürich, CH-8092 Zürich, Switzerland
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Turbulent mixing layers over cavities can couple with acoustic waves and lead to undesired oscillations. To understand the nonlinear aspects of this phenomenon, a turbulent mixing layer over a deep cavity is considered and its response to harmonic forcing is analysed with large-eddy simulations (LES) and linearised Navier–Stokes equations (LNSE). The Reynolds number is 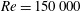$Re=150\,000$. As a model of incoming acoustic perturbations, spatially uniform time-harmonic velocity forcing is applied at the cavity end, with amplitudes spanning the wide range 0.045–8.9 % of the main channel bulk velocity. Compressible LES provide reference nonlinear responses of the shear layer, and the associated mean flows. Linear responses are calculated with the incompressible LNSE around the LES mean flows; they predict well the amplification (both measured with kinetic energy and with a proxy for vortex sound production in the mixing layer) and capture the nonlinear saturation observed as the forcing amplitude increases and the mixing layer thickens. Perhaps surprisingly, LNSE calculations based on a monochromatic (single-frequency) assumption yield a good agreement even though higher harmonics and their nonlinear interaction (Reynolds stresses) are not negligible. However, it is found that the leading Reynolds stresses do not force the mixing layer efficiently, as shown by a comparison with the optimal volume forcing obtained from a resolvent analysis. Therefore they cannot fully benefit from the potential for amplification available in the flow. Finally, the sensitivity of the optimal harmonic forcing at the cavity end is computed with an adjoint method. The sensitivities to mean flow modification and to a localised feedback (structural sensitivity) both identify the upstream cavity corner as the region where a small-amplitude modification has the strongest effect. This can guide in a systematic way the design of strategies aiming at controlling the amplification and saturation mechanisms.

JFM classification

Acoustics: Acoustics Instability: Instability Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 853 , 25 October 2018 , pp. 386 - 418
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Åkervik, E., Hœpffner, J., Ehrenstein, U. & Henningson, D. 2007 Optimal growth, model reduction and control in a separated boundary-layer flow using global eigenmodes. J. Fluid Mech. 579, 305–314.Google Scholar
del Álamo, J. C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.Google Scholar
Alvarez, J. O., Kerschen, E. J. & Tumin, A. 2004 A theoretical model for cavity acoustic resonances in subsonic flow. In 10th AIAA/CEAS Aeroacoustics Conference. American Institute of Aeronautics and Astronautics.Google Scholar
Barbagallo, A., Sipp, D. & Schmid, P. J. 2009 Closed-loop control of an open cavity flow using reduced-order models. J. Fluid Mech. 641, 1–50.Google Scholar
Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75 (5), 750–756.Google Scholar
Beneddine, S., Sipp, D., Arnault, A., Dandois, J. & Lesshafft, L. 2016 Conditions for validity of mean flow stability analysis. J. Fluid Mech. 798, 485–504.Google Scholar
Bottaro, A., Corbett, P. & Luchini, P. 2003 The effect of base flow variation on flow stability. J. Fluid Mech. 476, 293–302.Google Scholar
Boujo, E., Ehrenstein, U. & Gallaire, F. 2013 Open-loop control of noise amplification in a separated boundary layer flow. Phys. Fluids 25 (12), 124106.Google Scholar
Boujo, E. & Gallaire, F. 2015 Sensitivity and open-loop control of stochastic response in a noise amplifier flow: the backward-facing step. J. Fluid Mech. 762, 361–392.Google Scholar
Brandt, L., Sipp, D., Pralits, J. O. & Marquet, O. 2011 Effect of base-flow variation in noise amplifiers: the flat-plate boundary layer. J. Fluid Mech. 687, 503–528.Google Scholar
Cain, A. B., Bower, W. W., McCotter, F. & Romer, W. W.1996 Modeling and prediction of weapons bay acoustic amplitude and frequency. Tech. Rep. VEDA Inc.Google Scholar
Chomaz, J. M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.Google Scholar
Dergham, G., Sipp, D. & Robinet, J.-Ch. 2013 Stochastic dynamics and model reduction of amplifier flows: the backward facing step flow. J. Fluid Mech. 719, 406–430.Google Scholar
Edstrand, A. M., Davis, T. B., Schmid, P. J., Taira, K. & Cattafesta, L. N. 2016 On the mechanism of trailing vortex wandering. J. Fluid Mech. 801, R1.Google Scholar
Fani, A., Camarri, S. & Salvetti, M. V. 2012 Stability analysis and control of the flow in a symmetric channel with a sudden expansion. Phys. Fluids 24 (8), 084102.Google Scholar
Farrell, B. F. & Ioannou, P. J. 1993 Stochastic forcing of the linearized Navier–Stokes equations. Phys. Fluids A 5 (11), 2600–2609.Google Scholar
Garnaud, X., Lesshafft, L., Schmid, P. J. & Huerre, P. 2013 The preferred mode of incompressible jets: linear frequency response analysis. J. Fluid Mech. 716, 189–202.Google Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.Google Scholar
Gikadi, J., Föller, S. & Sattelmayer, T. 2014 Impact of turbulence on the prediction of linear aeroacoustic interactions: acoustic response of a turbulent shear layer. J. Sound Vib. 333, 6548–6559.Google Scholar
Graf, H. R. & Ziada, S. 2010 Excitation source of a side-branch shear layer. J. Sound Vib. 329, 2825–2842.Google Scholar
Gudmundsson, K. & Colonius, T. 2011 Instability wave models for the near-field fluctuations of turbulent jets. J. Fluid Mech. 689, 97–128.Google Scholar
Hecht, F. 2012 New development in FreeFem++. J. Numer. Maths 20 (3–4), 251–265.Google Scholar
Hill, D. C.1992 A theoretical approach for analyzing the restabilization of wakes. AIAA Paper 92-0067.Google Scholar
Howe, M. S. 1980 The dissipation of sound at an edge. J. Sound Vib. 70 (3), 407–411.Google Scholar
Hwang, Y. & Cossu, C. 2010 Amplification of coherent streaks in the turbulent Couette flow: an input–output analysis at low Reynolds number. J. Fluid Mech. 643, 333–348.Google Scholar
Iungo, G. V., Viola, F., Camarri, S., Porté-Agel, F. & Gallaire, F. 2013 Linear stability analysis of wind turbine wakes performed on wind tunnel measurements. J. Fluid Mech. 737, 499–526.Google Scholar
Kitsios, V., Cordier, L., Bonnet, J.-P., Ooi, A. & Soria, J. 2010 Development of a nonlinear eddy-viscosity closure for the triple-decomposition stability analysis of a turbulent channel. J. Fluid Mech. 664, 74–107.Google Scholar
Kooijman, G., Golliard, J. & Hirschberg, A. 2004 Orifice impedance under grazing flow measured with a single microphone method. In 10th AIAA/CEAS Aeroacoustics Conference. American Institute of Aeronautics and Astronautics.Google Scholar
Luchini, P. & Bottaro, A. 2014 Adjoint equations in stability analysis. Annu. Rev. Fluid Mech. 46 (1), 493–517.Google Scholar
Magri, L. & Juniper, M. P. 2013 Sensitivity analysis of a time-delayed thermo-acoustic system via an adjoint-based approach. J. Fluid Mech. 719, 183–202.Google Scholar
Mantič-Lugo, V., Arratia, C. & Gallaire, F. 2014 Self-consistent mean flow description of the nonlinear saturation of the vortex shedding in the cylinder wake. Phys. Rev. Lett. 113, 084501.Google Scholar
Mantič-Lugo, V. & Gallaire, F. 2016 Self-consistent model for the saturation mechanism of the response to harmonic forcing in the backward-facing step flow. J. Fluid Mech. 793, 777–797.Google Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.Google Scholar
Marquillie, M., Ehrenstein, U. & Laval, J.-P. 2011 Instability of streaks in wall turbulence with adverse pressure gradient. J. Fluid Mech. 681, 205–240.Google Scholar
McKeon, B. J., Sharma, A. S. & Jacobi, I. 2013 Experimental manipulation of wall turbulence: a systems approach. Phys. Fluids 25 (3), 031301.Google Scholar
Meliga, P. 2017 Harmonics generation and the mechanics of saturation in flow over an open cavity: a second-order self-consistent description. J. Fluid Mech. 826, 503–521.Google Scholar
Meliga, P., Pujals, G. & Serre, E. 2012 Sensitivity of 2-D turbulent flow past a D-shaped cylinder using global stability. Phys. Fluids 24 (6), 061701.Google Scholar
Meliga, P., Sipp, D. & Chomaz, J.-M. 2010 Open-loop control of compressible afterbody flows using adjoint methods. Phys. Fluids 22 (5), 054109.Google Scholar
Mettot, C., Sipp, D. & Bézard, H. 2014 Quasi-laminar stability and sensitivity analyses for turbulent flows: prediction of low-frequency unsteadiness and passive control. Phys. Fluids 26 (4).Google Scholar
Morris, S. C. 2011 Shear-layer instabilities: particle image velocimetry measurements and implications for acoustics. Annu. Rev. Fluid Mech. 43 (1), 529–550.Google Scholar
Nakiboğlu, G., Manders, H. B. M. & Hirschberg, A. 2012 Aeroacoustic power generated by a compact axysymmetric cavity: prediction of self-sustained oscillation and influence of the depth. J. Fluid Mech. 703, 163–191.Google Scholar
Oberleithner, K., Paschereit, C. O. & Wygnanski, I. 2014 On the impact of swirl on the growth of coherent structures. J. Fluid Mech. 741, 156–199.Google Scholar
Oberleithner, K., Schimek, S. & Paschereit, C. O. 2015 Shear flow instabilities in swirl-stabilized combustors and their impact on the amplitude dependent flame response: a linear stability analysis. Combust. Flame 162 (1), 86–99.Google Scholar
Piot, E., Casalis, G., Muller, F. & Bailly, C. 2006 Investigation of the PSE approach for subsonic and supersonic hot jets. Detailed comparisons with LES and linearized Euler equations results. Intl J. Aeroacoust. 5 (4), 361–393.Google Scholar
Poinsot, T., Yip, B., Veynante, D., Trouvé, A., Samaniego, J. M. & Candel, S. 1992 Active control: an investigation method for combustion instabilities. J. Phys. III 2 (7), 1331–1357.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Pujals, G., García-Villalba, M., Cossu, C. & Depardon, S. 2009 A note on optimal transient growth in turbulent channel flows. Phys. Fluids 21 (1), 015109.Google Scholar
Qadri, U. A. & Schmid, P. J. 2017 Frequency selection mechanisms in the flow of a laminar boundary layer over a shallow cavity. Phys. Rev. Fluids 2, 013902.Google Scholar
Reynolds, W. C. & Hussain, A. K. M. F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54, 263–288.Google Scholar
Rockwell, D. 1983 Oscillations of impinging shear layers. AIAA J. 21 (5), 645–664.Google Scholar
Rockwell, D. & Naudascher, E. 1978 Review – self-sustaining oscillations of flow past cavities. J. Fluids Engng 100 (2), 152–165.Google Scholar
Rockwell, D. & Naudascher, E. 1979 Self-sustained oscillations of impinging free shear layers. Annu. Rev. Fluid Mech. 11 (1), 67–94.Google Scholar
Rossiter, J. E.1964 Wind tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds. Tech. Rep. Aeronautical Research Council Reports and Memoranda.Google Scholar
Rowley, C. W. & Williams, D. R. 2006 Dynamics and control of high-Reynolds-number flow over open cavities. Annu. Rev. Fluid Mech. 38, 251–276.Google Scholar
Sipp, D. & Lebedev, A. 2007 Global stability of base and mean flows: a general approach and its applications to cylinder and open cavity flows. J. Fluid Mech. 593, 333–358.Google Scholar
Tam, C. K. W. & Block, P. J. W. 1978 On the tones and pressure oscillations induced by flow over rectangular cavities. J. Fluid Mech. 89 (2), 373–399.Google Scholar
Tammisola, O. & Juniper, M. P. 2016 Coherent structures in a swirl injector at Re = 4800 by nonlinear simulations and linear global modes. J. Fluid Mech. 792, 620–657.Google Scholar
Tonon, D., Hirschberg, A., Golliard, J. & Ziada, S. 2011 Aeroacoustics of pipe systems with closed branches. Intl J. Aeroacoust. 10 (2–3), 201–275.Google Scholar
Turton, S. E., Tuckerman, L. S. & Barkley, D. 2015 Prediction of frequencies in thermosolutal convection from mean flows. Phys. Rev. E 91, 043009.Google Scholar
Viola, F., Iungo, G. V., Camarri, S., Porté-Agel, F. & Gallaire, F. 2014 Prediction of the hub vortex instability in a wind turbine wake: stability analysis with eddy-viscosity models calibrated on wind tunnel data. J. Fluid Mech. 750, R1.Google Scholar