Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-01T03:52:02.069Z Has data issue: false hasContentIssue false
  • English
  • Français

The route to dissipation in strongly stratified and rotating flows

Published online by Cambridge University Press:  27 February 2013

Enrico Deusebio ,
A. Vallgren  and
E. Lindborg
Enrico Deusebio*
Affiliation:
Linné Flow Centre, Department of Mechanics, Royal Institute of Technology, Stockholm, 10044, Sweden
A. Vallgren
Affiliation:
Linné Flow Centre, Department of Mechanics, Royal Institute of Technology, Stockholm, 10044, Sweden
E. Lindborg
Affiliation:
Linné Flow Centre, Department of Mechanics, Royal Institute of Technology, Stockholm, 10044, Sweden
*
†Email address for correspondence: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate the route to dissipation in strongly stratified and rotating systems through high-resolution numerical simulations of the Boussinesq equations (BQs) and the primitive equations (PEs) in a triply periodic domain forced at large scales. By applying geostrophic scaling to the BQs and using the same horizontal length scale in defining the Rossby and the Froude numbers, 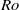$\mathit{Ro}$ and 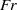$\mathit{Fr}$, we show that the PEs can be obtained from the BQs by taking the limit 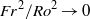${\mathit{Fr}}^{2} / {\mathit{Ro}}^{2} \rightarrow 0$. When 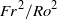${\mathit{Fr}}^{2} / {\mathit{Ro}}^{2} $ is small the difference between the results from the BQ and the PE simulations is shown to be small. For large rotation rates, quasi-geostrophic dynamics are recovered with a forward enstrophy cascade and an inverse energy cascade. As the rotation rate is reduced, a fraction of the energy starts to cascade towards smaller scales, leading to a shallowing of the horizontal spectra from 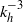${ k}_{h}^{- 3} $ to 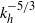${ k}_{h}^{- 5/ 3} $ at the small-scale end. The vertical spectra show a similar transition as the horizontal spectra and we find that Charney isotropy is approximately valid also at larger wavenumbers than the transition wavenumber. The high resolutions employed allow us to capture both ranges within the same simulation. At the transition scale, kinetic energy in the rotational and in the horizontally divergent modes attain comparable values. The divergent energy is several orders of magnitude larger than the quasi-geostrophic divergent energy given by the 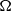$\Omega $-equation. The amount of energy cascading downscale is mainly controlled by the rotation rate, with a weaker dependence on the stratification. A larger degree of stratification favours a downscale energy cascade. For intermediate degrees of rotation and stratification, a constant energy flux and a constant enstrophy flux coexist within the same range of scales. In this range, the enstrophy flux is a result of triad interactions involving three geostrophic modes, while the energy flux is a result of triad interactions involving at least one ageostrophic mode, with a dominant contribution from interactions involving two ageostrophic and one geostrophic mode. Dividing the ageostrophic motions into two classes depending on the sign of the linear wave frequency, we show that the energy transfer is for the largest part supported by interactions within the same class, ruling out the wave–wave–vortex resonant triad interaction as a mean of the downscale energy transfer. The role of inertia-gravity waves is studied through analyses of time-frequency spectra of single Fourier modes. At large scales, distinct peaks at frequencies predicted for linear waves are observed, whereas at small scales no clear wave activity is observed. Triad interactions show a behaviour which is consistent with turbulent dynamics, with a large exchange of energy in triads with one small and two large comparable wavenumbers. The exchange of energy is mainly between the modes with two comparable wavenumbers.

JFM classification

Geophysical and Geological Flows: Geostrophic turbulence Turbulent Flows: Rotating turbulence Turbulent Flows: Stratified turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 720 , 10 April 2013 , pp. 66 - 103
Copyright
©2013 Cambridge University Press.

References

Augier, P., Chomaz, J.-M. & Billant, P. 2012 Spectral analysis of the transition to turbulence from a dipole in stratified fluids. J. Fluid Mech. 713, 86–108.CrossRefGoogle Scholar
Bartello, P. 1995 Geostrophic adjustment and inverse cascades in rotating stratified turbulence. J. Atmos. Sci. 52, 4410–4428.Google Scholar
Bartello, P. 2010 Quasigeostrophic and stratified turbulence in the atmosphere. In IUTAM Symposium on Turbulence in the Atmosphere and Oceans (ed. Dritschel, D.), IUTAM Bookseries (closed), vol. 28, pp. 117–130. Springer.CrossRefGoogle Scholar
Bellet, F., Godeferd, F. S., Scott, J. F. & Cambon, C. 2006 Wave turbulence in rapidly rotating flows. J. Fluid Mech. 562, 83–121.CrossRefGoogle Scholar
Billant, P. & Chomaz, J.-M. 2001 Self-similarity of strongly stratified inviscid flows. Phys. Fluids 13 (6), 1645–1651.CrossRefGoogle Scholar
Boer, G. J. & Shepherd, T. G. 1983 Large-scale two-dimensional turbulence in the atmosphere. J. Atmos. Sci. 40, 164–184.2.0.CO;2>CrossRefGoogle Scholar
Boffetta, G. & Musacchio, S. 2010 Evidence for the double cascade scenario in two-dimensional turbulence. Phys. Rev. E 82, 016307.CrossRefGoogle ScholarPubMed
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J.-M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.CrossRefGoogle Scholar
Cambon, C., Mansour, N. N. & Godeferd, F. S. 1997 Energy transfer in rotating turbulence. J. Fluid Mech. 337, 303–332.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 1988 Spectral methods in Fluid Dynamics. Springer.CrossRefGoogle Scholar
Charney, Jule G. 1971 Geostrophic turbulence. J. Atmos. Sci. 28 (6), 1087–1094.Google Scholar
Cho, J. Y. N. & Lindborg, E. 2001 Horizontal velocity structure functions in the upper troposphere and lower stratosphere 1. Observations. J. Geophys. Res. 106 (D10), 10223–10232.CrossRefGoogle Scholar
Ferrari, R. & Wunsch, C. 2009 Ocean circulation kinetic energy: reservoirs, sources, and sinks. Annu. Rev. Fluid Mech. 41, 253–282.CrossRefGoogle Scholar
Gargett, A. E., Hendricks, P. J., Sanford, T. B., Osborn, T. R. & Williams, A. J. 1981 A composite spectrum of vertical shear in the upper ocean. J. Phys. Oceanogr. 11, 1258–1271.Google Scholar
Garrett, C. & Munk, W. 1979 Internal waves in the ocean. Annu. Rev. Fluid Mech. 11, 339–369.CrossRefGoogle Scholar
Gill, A. E. 1982 Atmosphere–Ocean Dynamics. Academic.Google Scholar
Godeferd, F. S. & Cambon, C. 1994 Detailed investigation of energy transfers in homogeneous stratified turbulence. Phys. Fluids 6 (6), 2084–2100.Google Scholar
Hamilton, K., Takahashi, Y. O. & Ohfuchi, W. 2008 Mesoscale spectrum of atmospheric motions investigated in a very fine resolution global general circulation model. J. Geophys. Res. 113 (18).Google Scholar
Kitamura, Y. & Matsuda, Y. 2006 The ${ k}_{H}^{- 3} $ and ${ k}_{H}^{- 5/ 3} $ energy spectra in stratified turbulence. Geophys. Res. Lett. 33, L05809.Google Scholar
Kraichnan, R. H. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10 (7), 1417–1423.CrossRefGoogle Scholar
Leith, C. E. & Kraichnan, R. H. 1972 Predictability of turbulent flows. J. Atmos. Sci. 29, 1041–1058.2.0.CO;2>CrossRefGoogle Scholar
Lelong, M.-P. & Riley, J. J. 1991 Internal wave-vortical mode interactions in strongly stratified flows. J. Fluid Mech. 232, 1–19.CrossRefGoogle Scholar
Lilly, D. K. 1983 Stratified turbulence and the mesoscale variability of the atmosphere. J. Atmos. Sci. 40 (3), 749–761.Google Scholar
Lindborg, E. 2006 The energy cascade in a strongly stratified fluid. J. Fluid Mech. 550, 207–242.CrossRefGoogle Scholar
Lindborg, E. 2007 Horizontal wavenumber spectra of vertical vorticity and horizontal divergence in the upper troposphere and lower stratosphere. J. Atmos. Sci. 64, 1017.Google Scholar
Lindborg, E. & Brethouwer, G. 2007 Stratified turbulence forced in rotational and divergent modes. J. Fluid Mech. 586, 83–108.CrossRefGoogle Scholar
Lvov, Y. V., Polzin, K. L. & Yokoyama, N. 2011 Resonant and near-resonant internal wave interactions. J. Phys. Oceanogr. 42 (5), 669–691. ArXiv e-prints.CrossRefGoogle Scholar
Maltrud, M. E. & Vallis, G. K. 1993 Energy and enstrophy transfer in numerical simulations of two-dimensional turbulence. Phys. Fluids 5, 1760–1775.CrossRefGoogle Scholar
McComas, C. H. & Bretherton, F. P. 1977 Resonant interaction of oceanic internal waves. J. Geophys. Res. 82, 1397–1412.CrossRefGoogle Scholar
McWilliams, James C. 2010 A perspective on submesoscale geophysical turbulence. In IUTAM Symposium on Turbulence in the Atmosphere and Oceans (ed. Dritschel, D.), IUTAM Bookseries (closed), vol. 28, pp. 131–141. Springer.CrossRefGoogle Scholar
Ménesguen, C., Hua, B. L., Papenberg, C., Klaeschen, D., Géli, L. & Hobbs, R. 2009 Effect of bandwidth on seismic imaging of rotating stratified turbulence surrounding an anticyclonic eddy from field data and numerical simulations. Geophys. Res. Lett. 360.Google Scholar
Molemaker, M. J. & McWilliams, J. C. 2010 Local balance and cross-scale flux of available potential energy. J. Fluid Mech. 645, 295–314.CrossRefGoogle Scholar
Molemaker, M. J., McWilliams, J. C. & Capet, X. 2010 Balanced and unbalanced routes to dissipation in an equilibrated Eady flow. J. Fluid Mech. 654, 35–63.Google Scholar
Molemaker, M. J., McWilliams, J. C. & Yavneh, I. 2005 Baroclinic instability and loss of balance. J. Phys. Ocean. 35, 1505–1517.CrossRefGoogle Scholar
Muller, P., McWilliams, J. C. & Molemaker, M. J. 2005 Routes to dissipation in the ocean: the 2D/3D turbulence conundrum. In Marine Turbulence: Theories, Observations, and Models (ed. Baumert, H. Z., Simpson, J. & Sündermann, J.), pp. 397–405. Cambridge University Press.Google Scholar
Munk, W. 1981 Internal waves and small-scale processes. Evol. Phys. Oceanogr. 264–291.Google Scholar
Nastrom, G. D. & Gage, K. S. 1985 A climatology of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft. J. Atmos. Sci. 42, 950–960.2.0.CO;2>CrossRefGoogle Scholar
Nikurashin, M. & Ferrari, R. 2011 Global energy conversion rate from geostrophic flows into internal lee waves in the deep ocean. Geophys. Res. Lett. 38, 8610.Google Scholar
Ohkitani, K. 1990 Non-locality in a forced two-dimensional turbulence. Phys. Fluids A 2 (9), 1529–1531.CrossRefGoogle Scholar
Ohkitani, K. & Kida, S. 1992 Triad interactions in a forced turbulence. Phys. Fluids A 4 (4), 794–802.CrossRefGoogle Scholar
Pedlosky, J. 1987 Geophysical Fluid Dynamics. Springer.CrossRefGoogle Scholar
Phillips, O. M. 1981 Wave interactions – the evolution of an idea. J. Fluid Mech. 106, 215–227.CrossRefGoogle Scholar
Polzin, K. L. & Lvov, Y. V. 2011 Toward regional characterizations of the oceanic internal wavefield. Rev. Geophys. 49, 4003.CrossRefGoogle Scholar
Riley, J. J. & deBruynKops, S. M. 2003 Dynamics of turbulence strongly influenced by buoyancy. Phys. Fluids 15 (7), 2047–2059.CrossRefGoogle Scholar
Scott, R. K. 2007 Nonrobustness of the two-dimensional turbulent inverse cascade. Phys. Rev. E 75, 046301.CrossRefGoogle ScholarPubMed
Skamarock, W. C. 2004 Evaluating mesoscale NWP models using kinetic energy spectra. Mon. Weath. Rev. 132 (12), 3019–3032.CrossRefGoogle Scholar
Staquet, C. & Sommeria, J. 2002 Internal gravity waves: from instabilities to turbulence. Annu. Rev. Fluid Mech. 34, 559–593.CrossRefGoogle Scholar
Takahashi, Y. O., Hamilton, K. & Ohfuchi, W. 2006 Explicit global simulation of the mesoscale spectrum of atmospheric motions. Geophys. Res. Lett. 33, L12812.Google Scholar
Vallgren, A. 2011 Infrared reynolds number dependency of the two-dimensional inverse energy cascade. J. Fluid Mech. 667, 463–473.Google Scholar
Vallgren, A., Deusebio, E. & Lindborg, E. 2011 A possible explanation of the atmospheric kinetic and potential energy spectra. Phys. Rev. Lett. 99, 99–101.Google Scholar
Vallgren, A. & Lindborg, E. 2010 Charney isotropy and equipartition in quasi-geostrophic turbulence. J. Fluid Mech. 656, 448–457.Google Scholar
Vallgren, A. & Lindborg, E. 2011 The enstrophy cascade in forced two-dimensional turbulence. J. Fluid Mech. 671, 168–183.CrossRefGoogle Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-scale Circulation (electronic version). Cambridge University Press.CrossRefGoogle Scholar
Viúdez, Á. & Dritschel, D. G. 2006 Spontaneous generation of inertiagravity wave packets by balanced geophysical flows. J. Fluid Mech. 553, 107–117.CrossRefGoogle Scholar
Waite, M. L. & Bartello, P. 2004 Stratified turbulence dominated by vortical motion. J. Fluid Mech. 517, 281–308.CrossRefGoogle Scholar
Waite, M. L. & Bartello, P. 2006 The transition from geostrophic to stratified turbulence. J. Fluid Mech. 568, 89–108.CrossRefGoogle Scholar
Waite, M. L. & Snyder, C. 2009 The mesoscale kinetic energy spectrum of a baroclinic life cycle. J. Atmos. Sci. 66, 883.CrossRefGoogle Scholar
Wunsch, C. & Ferrari, R. 2004 Vertical mixing, energy, and the general circulation of the oceans. Annu. Rev. Fluid Mech. 36, 281–314.CrossRefGoogle Scholar