Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-12-02T22:04:37.823Z Has data issue: false hasContentIssue false
  • English
  • Français

Rough-wall turbulent boundary layers with constant skin friction

Published online by Cambridge University Press:  28 March 2017

A. Sridhar Open the ORCID record for A. Sridhar [Opens in a new window] ,
D. I. Pullin  and
W. Cheng Open the ORCID record for W. Cheng [Opens in a new window]
A. Sridhar*
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, Pasadena, CA 91125, USA
D. I. Pullin
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, Pasadena, CA 91125, USA
W. Cheng
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, Pasadena, CA 91125, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A semi-empirical model is presented that describes the development of a fully developed turbulent boundary layer in the presence of surface roughness with length scale 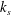$k_{s}$ that varies with streamwise distance $x$. Interest is centred on flows for which all terms of the von Kármán integral relation, including the ratio of outer velocity to friction velocity 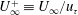$U_{\infty }^{+}\equiv U_{\infty }/u_{\unicode[STIX]{x1D70F}}$, are streamwise constant. For 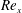$Re_{x}$ assumed large, use is made of a simple log-wake model of the local turbulent mean-velocity profile that contains a standard mean-velocity correction for the asymptotic fully rough regime and with assumed constant parameter values. It is then shown that, for a general power-law external velocity variation 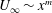$U_{\infty }\sim x^{m}$, all measures of the boundary-layer thickness must be proportional to $x$ and that the surface sand-grain roughness scale variation must be the linear form 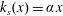$k_{s}(x)=\unicode[STIX]{x1D6FC}x$, where $x$ is the distance from the boundary layer of zero thickness and $\unicode[STIX]{x1D6FC}$ is a dimensionless constant. This is shown to give a two-parameter 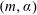$(m,\unicode[STIX]{x1D6FC})$ family of solutions, for which 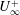$U_{\infty }^{+}$ (or equivalently 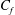$C_{f}$) and boundary-layer thicknesses can be simply calculated. These correspond to perfectly self-similar boundary-layer growth in the streamwise direction with similarity variable 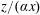$z/(\unicode[STIX]{x1D6FC}x)$, where $z$ is the wall-normal coordinate. Results from this model over a range of $\unicode[STIX]{x1D6FC}$ are discussed for several cases, including the zero-pressure-gradient (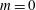$m=0$) and sink-flow (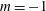$m=-1$) boundary layers. Trends observed in the model are supported by wall-modelled large-eddy simulation of the zero-pressure-gradient case for 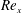$Re_{x}$ in the range 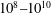$10^{8}{-}10^{10}$ and for four values of $\unicode[STIX]{x1D6FC}$. Linear streamwise growth of the displacement, momentum and nominal boundary-layer thicknesses is confirmed, while, for each $\unicode[STIX]{x1D6FC}$, the mean-velocity profiles and streamwise turbulent variances are found to collapse reasonably well onto 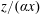$z/(\unicode[STIX]{x1D6FC}x)$. For given $\unicode[STIX]{x1D6FC}$, calculations of 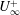$U_{\infty }^{+}$ obtained from large-eddy simulations are streamwise constant and independent of 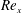$Re_{x}$ when this is large. The present results suggest that, in the sense that 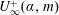$U_{\infty }^{+}(\unicode[STIX]{x1D6FC},m)$ is constant, these flows can be interpreted as the fully rough limit for boundary layers in the presence of small-scale linear roughness.

JFM classification

Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 818 , 10 May 2017 , pp. 26 - 45
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Mechanical Engineering, Physical Sciences and Engineering Division, King Abdullah University of Science and Technology, Thuwal, Saudi Arabia, 23955-6900.

References

Cheng, W., Pullin, D. I. & Samtaney, R. 2015 Large-eddy simulation of separation and reattachment of a flat plate turbulent boundary layer. J. Fluid Mech. 785, 78–108.CrossRefGoogle Scholar
Chung, D. & Pullin, D. I. 2009 Large-eddy simulation and wall-modeling of turbulent chanel flow. J. Fluid Mech. 631, 281–309.CrossRefGoogle Scholar
Clauser, F. H. 1954 Turbulent boundary layers in adverse pressure gradients. J. Aero. Sci. 21, 91–108.Google Scholar
Colebrook, C. F. 1939 Turbulent flow in pipes, with particular reference to the transition region between the smooth and rough pipe laws. J. Inst. Civil Engrs Lond. 11, 133–156.CrossRefGoogle Scholar
Coles, D. 1956 The law of the wake in the turbulent boundary layer. J. Fluid Mech. 1 (2), 191–226.CrossRefGoogle Scholar
Coles, D. 1957 Remarks on the equilibrium turbulent boundary layer. J. Aero. Sci. 24, 495–506.Google Scholar
Granville, P. S. 1958 The frictional resistance and turbulent boundary layer of rough surfaces. J. Ship Res. 2, 52–74.CrossRefGoogle Scholar
Inoue, M. & Pullin, D. I. 2011 Large-eddy simulation of the zero-pressure-gradient turbulent boundary layer up to Re 𝜃 = O (1012). J. Fluid Mech. 686, 507–533.CrossRefGoogle Scholar
Jewkes, J. W., Chung, Y. M. & Carpenter, P. W. 2011 Modification to a turbulent inflow generation method for boundary-layer flows. AIAA J. 49 (1), 247–250.CrossRefGoogle Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36 (1), 173–196.CrossRefGoogle Scholar
Jones, M. B., Marusic, I. & Perry, A. E. 2001 Evolution and structure of sink-flow turbulent boundary layers. J. Fluid Mech. 428, 1–27.CrossRefGoogle Scholar
Kameda, T., Mochizuki, S., Osaka, H. & Higaki, K. 2008 Realization of the turbulent boundary layer over the rough wall satisfied the conditions of complete similarity and its mean flow quantities. J. Fluid Sci. Technol. 3 (1), 31–42.CrossRefGoogle Scholar
Krogstad, P.-Å., Antonia, R. A. & Browne, L. W. B. 1992 Comparison between rough- and smooth-wall turbulent boundary layers. J. Fluid Mech. 245, 599–617.CrossRefGoogle Scholar
Lund, T. S., Wu, X. & Squires, K. D. 1998 Generation of turbulent inflow data for spatially-developing boundary layer simulations. J. Comput. Phys. 140 (2), 233–258.CrossRefGoogle Scholar
Lundgren, T. S. 1982 Strained spiral vortex model for turbulent fine structure. Phys. Fluids 25, 2193–2203.CrossRefGoogle Scholar
Misra, A. & Pullin, D. I. 1997 A vortex-based subgrid stress model for large-eddy simulation. Phys. Fluids 9, 2443–2454.CrossRefGoogle Scholar
Moody, L. F. 1944 Friction factors for pipe flow. Trans. ASME 66 (8), 671–684.Google Scholar
Nikuradse, J.1933 Law of the wall in rough pipes. NASA Tech. Memo. 1292.Google Scholar
Perot, J. B. 1993 An analysis of the fractional step method. J. Comput. Phys. 108, 51–58.CrossRefGoogle Scholar
Pope, S. B. 2002 Turbulent Flows. Cambridge University Press.Google Scholar
Prandtl, L. & Schlichting, H. 1934 Das widerstandsgesetz rauher platten. Werft, Reederei, Hafen 15 (1), 4.Google Scholar
Rotta, J. C. 1962 Turbulent boundary layers in incompressible flow. Prog. Aerosp. Sci. 2 (1), 1–219.CrossRefGoogle Scholar
Saito, N., Pullin, D. I. & Inoue, M. 2012 Large eddy simulation of smooth-wall, transitional and fully rough-wall channel flow. Phys. Fluids 24 (7), 075103.CrossRefGoogle Scholar
Spalart, P. R., Moser, R. D. & Rogers, M. M. 1991 Spectral methods for the Navier–Stokes equations with one infinite and two periodic directions. J. Comput. Phys. 96, 297–324.CrossRefGoogle Scholar
Squire, D. T., Morrill-Winter, C., Hutchins, N., Schultz, M. P., Klewicki, J. C. & Marusic, I. 2016 Comparison of turbulent boundary layers over smooth and rough surfaces up to high Reynolds numbers. J. Fluid Mech. 795, 210–240.CrossRefGoogle Scholar
Talluru, K. M., Djenidi, L., Kamruzzaman, Md. & Antonia, R. A. 2016 Self preservation in a zero pressure gradient rough-wall turbulent boundary layer. J. Fluid Mech. 788, 57–69.CrossRefGoogle Scholar