Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-25T01:36:01.413Z Has data issue: false hasContentIssue false
  • English
  • Français

Roughness effects in turbulent forced convection

Published online by Cambridge University Press:  19 December 2018

M. MacDonald Open the ORCID record for M. MacDonald [Opens in a new window] ,
N. Hutchins  and
D. Chung Open the ORCID record for D. Chung [Opens in a new window]
M. MacDonald*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
N. Hutchins
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
D. Chung
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We conducted direct numerical simulations of turbulent flow over three-dimensional sinusoidal roughness in a channel. A passive scalar is present in the flow with Prandtl number 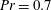$Pr=0.7$, to study heat transfer by forced convection over this rough surface. The minimal-span channel is used to circumvent the high cost of simulating high-Reynolds-number flows, which enables a range of rough surfaces to be efficiently simulated. The near-wall temperature profile in the minimal-span channel agrees well with that of the conventional full-span channel, indicating that it can be readily used for heat-transfer studies at a much reduced cost compared to conventional direct numerical simulation. As the roughness Reynolds number, 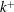$k^{+}$, is increased, the Hama roughness function, 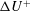$\unicode[STIX]{x0394}U^{+}$, increases in the transitionally rough regime before tending towards the fully rough asymptote of 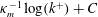$\unicode[STIX]{x1D705}_{m}^{-1}\log (k^{+})+C$, where 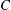$C$ is a constant that depends on the particular roughness geometry and 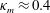$\unicode[STIX]{x1D705}_{m}\approx 0.4$ is the von Kármán constant. In this fully rough regime, the skin-friction coefficient is constant with bulk Reynolds number, 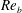$Re_{b}$. Meanwhile, the temperature difference between smooth- and rough-wall flows, 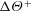$\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}^{+}$, appears to tend towards a constant value, 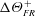$\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}_{FR}^{+}$. This corresponds to the Stanton number (the temperature analogue of the skin-friction coefficient) monotonically decreasing with 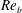$Re_{b}$ in the fully rough regime. Using shifted logarithmic velocity and temperature profiles, the heat-transfer law as described by the Stanton number in the fully rough regime can be derived once both the equivalent sand-grain roughness 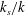$k_{s}/k$ and the temperature difference 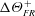$\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}_{FR}^{+}$ are known. In meteorology, this corresponds to the ratio of momentum and heat-transfer roughness lengths, 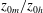$z_{0m}/z_{0h}$, being linearly proportional to the inner-normalised momentum roughness length, 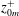$z_{0m}^{+}$, where the constant of proportionality is related to 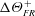$\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}_{FR}^{+}$. While Reynolds analogy, or similarity between momentum and heat transfer, breaks down for the bulk skin-friction and heat-transfer coefficients, similar distribution patterns between the heat flux and viscous component of the wall shear stress are observed. Instantaneous visualisations of the temperature field show a thin thermal diffusive sublayer following the roughness geometry in the fully rough regime, resembling the viscous sublayer of a contorted smooth wall.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 861 , 25 February 2019 , pp. 138 - 162
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andreas, E. L. 1987 A theory for the scalar roughness and the scalar transfer coefficients over snow and sea ice. Boundary-Layer Meteorol. 38, 159–184.Google Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2014 Velocity statistics in turbulent channel flow up to Re 𝜏 = 4000. J. Fluid Mech. 742, 171–191.Google Scholar
Bird, R. B., Stewart, W. E. & Lightfoot, E. N. 2002 Transport Phenomena, 2nd edn. Wiley.Google Scholar
Breugem, W. P., Boersma, B. J. & Uittenbogaard, R. E. 2006 The influence of wall permeability on turbulent channel flow. J. Fluid Mech. 562, 35–72.Google Scholar
Brutsaert, W. 1975 The roughness length for water vapor sensible heat, and other scalars. J. Atmos. Sci. 32, 2028–2031.Google Scholar
Busse, A., Thakkar, M. & Sandham, N. D. 2017 Reynolds-number dependence of the near-wall flow over irregular rough surfaces. J. Fluid Mech. 810, 196–224.Google Scholar
Cebeci, T. & Bradshaw, P. 1984 Physical and Computational Aspects of Convective Heat Transfer. Springer.Google Scholar
Chamberlain, A. C. 1966 Transport of gases to and from grass and grass-like surfaces. Proc. R. Soc. Lond. A 290, 236–265.Google Scholar
Chan, L., MacDonald, M., Chung, D., Hutchins, N. & Ooi, A. 2015 A systematic investigation of roughness height and wavelength in turbulent pipe flow in the transitionally rough regime. J. Fluid Mech. 771, 743–777.Google Scholar
Chung, D., Chan, L., MacDonald, M., Hutchins, N. & Ooi, A. 2015 A fast direct numerical simulation method for characterising hydraulic roughness. J. Fluid Mech. 773, 418–431.Google Scholar
Chung, D. & Matheou, G. 2012 Direct numerical simulation of stationary homogeneous stratified sheared turbulence. J. Fluid Mech. 696, 434–467.Google Scholar
Coceal, O. & Belcher, S. E. 2004 A canopy model of mean winds through urban areas. Q. J. R. Meteorol. Soc. 130, 1349–1372.Google Scholar
Dean, R. B. 1978 Reynolds number dependence of skin friction and other bulk flow variables in two-dimensional rectangular duct flow. J. Fluids Engng 100, 215–223.Google Scholar
Dipprey, D. F. & Sabersky, R. H. 1963 Heat and momentum transfer in smooth and rough tubes at various Prandtl numbers. Intl J. Heat Mass Transfer 6, 329–353.Google Scholar
Finnigan, J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32, 519–571.Google Scholar
Flack, K. A. & Schultz, M. P. 2014 Roughness effects on wall-bounded turbulent flows. Phys. Fluids 26, 101305.Google Scholar
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22, 071704.Google Scholar
Garratt, J. R. & Hicks, B. B. 1973 Momentum, heat and water vapour transfer to and from natural and artificial surfaces. Q. J. R. Meteorol. Soc. 99, 680–687.Google Scholar
Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.Google Scholar
Ham, F. & Iaccarino, G. 2004 Energy conservation in collocated discretization schemes on unstructured meshes. In Annual Research Briefs 2004, pp. 3–14. Center for Turbulence Research, Stanford University/NASA Ames.Google Scholar
Hama, F. R. 1954 Boundary-layer characteristics for smooth and rough surfaces. Trans. Soc. Nav. Archit. Mar. Engrs 62, 333–358.Google Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.Google Scholar
Kader, B. A. 1981 Temperature and concentration profiles in fully turbulent boundary layers. Intl J. Heat Mass Transfer 24, 1541–1544.Google Scholar
Kasagi, N., Tomita, Y. & Kuroda, A. 1992 Direct numerical simulation of passive scalar field in a turbulent channel flow. Trans. ASME J. Heat Transfer 114, 598–606.Google Scholar
Kawamura, H., Abe, H. & Matsuo, Y. 1999 DNS of turbulent heat transfer in channel flow with respect to Reynolds and Prandtl number effects. Intl J. Heat Fluid Flow 20, 196–207.Google Scholar
Kawamura, H., Ohsaka, K., Abe, H. & Yamamoto, K. 1998 DNS of turbulent heat transfer in channel flow with low to medium-high Prandtl number fluid. Intl J. Heat Fluid Flow 19, 482–491.Google Scholar
Kays, W. M., Crawford, M. E. & Weigand, B. 2005 Convective Heat and Mass Transfer, 4th edn. McGraw-Hill.Google Scholar
Kim, J. & Moin, P. 1989 Transport of passive scalars in a turbulent channel flow. In Turbulent Shear Flows, vol. 6, pp. 85–96. Springer.Google Scholar
Kozul, M., Chung, D. & Monty, J. P. 2016 Direct numerical simulation of the incompressible temporally developing turbulent boundary layer. J. Fluid Mech. 796, 437–472.Google Scholar
Kraichnan, R. H. 1962 Turbulent thermal convection at arbitrary Prandtl number. Phys. Fluids 5, 1374–1389.Google Scholar
Leonardi, S., Orlandi, P. & Antonia, R. A. 2007 Heat transfer in a turbulent channel flow with roughness. In Proc. 5th Intl Symp. on Turbulence and Shear Flow, Munich, Germany, pp. 785–790.Google Scholar
MacDonald, M., Chan, L., Chung, D., Hutchins, N. & Ooi, A. 2016 Turbulent flow over transitionally rough surfaces with varying roughness density. J. Fluid Mech. 804, 130–161.Google Scholar
MacDonald, M., Chung, D., Hutchins, N., Chan, L., Ooi, A. & García-Mayoral, R. 2017 The minimal-span channel for rough-wall turbulent flows. J. Fluid Mech. 816, 5–42.Google Scholar
Macdonald, R. W., Griffiths, R. F. & Hall, D. J. 1998 An improved method for the estimation of surface roughness of obstacle arrays. Atmos. Environ. 32, 1857–1864.Google Scholar
Mahesh, K., Constantinescu, G. & Moin, P. 2004 A numerical method for large-eddy simulation in complex geometries. J. Comput. Phys. 197, 215–240.Google Scholar
Miyake, Y., Tsujimoto, K. & Nakaji, M. 2001 Direct numerical simulation of rough-wall heat transfer in a turbulent channel flow. Intl J. Heat Fluid Flow 22, 237–244.Google Scholar
Nagib, H. M. & Chauhan, K. A. 2008 Variations of von Kármán coefficient in canonical flows.. Phys. Fluids 20, 101518.Google Scholar
Ng, C. S., Ooi, A., Lohse, D. & Chung, D. 2017 Changes in the boundary-layer structure at the edge of the ultimate regime in vertical natural convection. J. Fluid Mech. 825, 550–572.Google Scholar
Nikora, V., Goring, D., McEwan, I. & Griffiths, G. 2001 Spatially averaged open-channel flow over rough bed. J. Hydraul. Engng 127, 123–133.Google Scholar
Nikuradse, J.1933 Laws of flow in rough pipes. English transl. 1950, NACA Tech. Mem. 1292.Google Scholar
Owen, P. R. & Thomson, W. R. 1963 Heat transfer across rough surfaces. J. Fluid Mech. 15, 321–334.Google Scholar
Pirozzoli, S., Bernardini, M. & Orlandi, P. 2016 Passive scalars in turbulent channel flow at high Reynolds number. J. Fluid Mech. 788, 614–639.Google Scholar
Raupach, M. R., Antonia, R. A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44, 1–25.Google Scholar
Schultz, M. P. & Flack, K. A. 2009 Turbulent boundary layers on a systematically varied rough wall. Phys. Fluids 21, 015104.Google Scholar
Schultz, M. P. & Flack, K. A. 2013 Reynolds-number scaling of turbulent channel flow. Phys. Fluids 25, 025104.Google Scholar
Sekimoto, A., Dong, S. & Jiménez, J. 2016 Direct numerical simulation of statistically stationary and homogeneous shear turbulence and its relation to other shear flows. Phys. Fluids 28, 035101.Google Scholar
Tiselj, I., Bergant, R., Mavko, B., Bajsić, I. & Hetsroni, G. 2001 DNS of turbulent heat transfer in channel flow with heat conduction in the solid wall. Trans. ASME J. Heat Transfer 123, 849–857.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Webb, R. L. 1981 Performance evaluation criteria for use of enhanced heat transfer surfaces in heat exchanger design. Intl J. Heat Fluid Flow 24, 715–726.Google Scholar
Wood, N. & Mason, P. 1991 The influence of static stability on the effective roughness lengths for momentum and heat transfer. Q. J. R. Meteorol. Soc. 117, 1025–1056.Google Scholar
Yaglom, A. M. 1979 Similarity laws for constant-pressure and pressure-gradient turbulent wall flows. Annu. Rev. Fluid Mech. 11, 505–540.Google Scholar