Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T19:21:40.633Z Has data issue: false hasContentIssue false
  • English
  • Français

Rotations and accumulation of ellipsoidal microswimmers in isotropic turbulence

Published online by Cambridge University Press:  12 January 2018

N. Pujara Open the ORCID record for N. Pujara [Opens in a new window] ,
M. A. R. Koehl  and
E. A. Variano
N. Pujara*
Affiliation:
Department of Civil and Engineering, University of California, Berkeley, CA 94720, USA
M. A. R. Koehl
Affiliation:
Department of Integrative Biology, University of California, Berkeley, CA 94720, USA
E. A. Variano
Affiliation:
Department of Civil and Engineering, University of California, Berkeley, CA 94720, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Aquatic micro-organisms and artificial microswimmers locomoting in turbulent flow encounter velocity gradients that rotate them, thereby changing their swimming direction and possibly providing cues about the local flow environment. Using numerical simulations of ellipsoidal particles in isotropic turbulence, we investigate the effects of body shape and swimming velocity on particle motion. 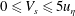Four particle shapes (sphere, rod, disc and triaxial ellipsoid) are investigated at five different swimming velocities in the range $0\leqslant V_{s}\leqslant 5u_{\unicode[STIX]{x1D702}}$, where $V_{s}$ is the swimming velocity and 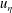$u_{\unicode[STIX]{x1D702}}$ is the Kolmogorov velocity scale. We find that anisotropic, swimming particles preferentially sample regions of lower fluid vorticity than passive particles do, and hence they accumulate in these regions. While this effect is monotonic with swimming velocity, the particle enstrophy (variance of particle angular velocity) varies non-monotonically with swimming velocity. In contrast to passive particles, the particle enstrophy is a function of shape for swimming particles. The particle enstrophy is largest for triaxial ellipsoids swimming at a velocity smaller than 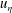$u_{\unicode[STIX]{x1D702}}$. We also observe that the average alignment of particles with the directions of the velocity gradient tensor are altered by swimming leading to a more equal distribution of rotation about different particle axes.

JFM classification

Turbulent Flows: Isotropic turbulence Biological Fluid Dynamics: Micro-organism dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 838 , 10 March 2018 , pp. 356 - 368
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Byron, M., Einarsson, J., Gustavsson, K., Voth, G., Mehlig, B. & Variano, E. 2015 Shape-dependence of particle rotation in isotropic turbulence. Phys. Fluids 27, 035101.CrossRefGoogle Scholar
Chevillard, L. & Meneveau, C. 2013 Orientation dynamics of small, triaxial–ellipsoidal particles in isotropic turbulence. J. Fluid Mech. 737, 571–596.Google Scholar
De Lillo, F., Cencini, M., Durham, W. M., Barry, M., Stocker, R., Climent, E. & Boffetta, G. 2014 Turbulent fluid acceleration generates clusters of gyrotactic microorganisms. Phys. Rev. Lett. 112, 044502.Google Scholar
Dreyfus, R., Baudry, J., Roper, M. L., Fermigier, M., Stone, H. A. & Bibette, J. 2005 Microscopic artificial swimmers. Nature 437, 862–865.CrossRefGoogle ScholarPubMed
Durham, W. M., Climent, E., Barry, M., De Lillo, F., Boffetta, G., Cencini, M. & Stocker, R. 2013 Turbulence drives microscale patches of motile phytoplankton. Nature Commun. 4, 2148.CrossRefGoogle ScholarPubMed
Durham, W. M., Kessler, J. O. & Stocker, R. 2009 Disruption of vertical motility by shear triggers formation of thin phytoplankton layers. Science 323, 1067–1070.CrossRefGoogle ScholarPubMed
Dusenbery, D. B. 2009 Living at Micro Scale: The Unexpected Physics of being Small. Harvard University Press.Google Scholar
Fouxon, I. & Leshansky, A. 2015 Phytoplankton’s motion in turbulent ocean. Phys. Rev. E 92, 013017.Google Scholar
Fuchs, H. L. & Gerbi, G. P. 2016 Seascape-level variation in turbulence- and wave-generated hydrodynamic signals experienced by plankton. Prog. Oceanogr. 141, 109–129.Google Scholar
Guasto, J. S., Rusconi, R. & Stocker, R. 2012 Fluid mechanics of planktonic microorganisms. Annu. Rev. Fluid Mech. 44, 373–400.Google Scholar
Gustavsson, K., Berglund, F., Jonsson, P. R. & Mehlig, B. 2016 Preferential sampling and small-scale clustering of gyrotactic microswimmers in turbulence. Phys. Rev. Lett. 116, 108104.Google Scholar
ten Hagen, B., Kümmel, F., Wittkowski, R., Takagi, D., Löwen, H. & Bechinger, C. 2014 Gravitaxis of asymmetric self-propelled colloidal particles. Nature Communications 5, 4829.CrossRefGoogle ScholarPubMed
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 161–179.Google Scholar
Kessler, J. O. 1985 Hydrodynamic focusing of motile algal cells. Nature 313, 218–220.Google Scholar
Khurana, N., Blawzdziewicz, J. & Ouellette, N. T. 2011 Reduced transport of swimming particles in chaotic flow due to hydrodynamic trapping. Phys. Rev. Lett. 106, 198104.Google Scholar
Khurana, N. & Ouellette, N. T. 2012 Interactions between active particles and dynamical structures in chaotic flow. Phys. Fluids 24, 091902.Google Scholar
Kiørboe, T. 2008 A Mechanistic Approach to Plankton Ecology. Princeton University Press.Google Scholar
Koehl, M. A. R. & Cooper, T. 2015 Swimming in an unsteady world. Integr. Compar. Biol. 55, 683–697.Google Scholar
Kramel, S., Voth, G. A., Tympel, S. & Toschi, F. 2016 Preferential rotation of chiral dipoles in isotropic turbulence. Phys. Rev. Lett. 117, 154501.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26, 883–889.Google Scholar
Ni, R., Ouellette, N. T. & Voth, G. A. 2014 Alignment of vorticity and rods with Lagrangian fluid stretching in turbulence. J. Fluid Mech. 743, R3.CrossRefGoogle Scholar
Parsa, S., Calzavarini, E., Toschi, F. & Voth, G. A. 2012 Rotation rate of rods in turbulent fluid flow. Phys. Rev. Lett. 109, 134501.Google Scholar
Perlman, E., Burns, R., Li, Y. & Meneveau, C. 2007 Data exploration of turbulence simulations using a database cluster. In Proceedings of the 2007 ACM/IEEE Conference on Supercomputing Series: SC ’07, Reno, NV, ACM.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Pujara, N. & Variano, E. A. 2017 Rotations of small, inertialess triaxial ellipsoids in isotropic turbulence. J. Fluid Mech. 821, 517–538.Google Scholar
Takatori, S. C., Yan, W. & Brady, J. F. 2014 Swim pressure: stress generation in active matter. Phys. Rev. Lett. 113, 028103.Google Scholar
Torney, C. & Neufeld, Z. 2007 Transport and aggregation of self-propelled particles in fluid flows. Phys. Rev. Lett. 99, 078101.Google Scholar
Underhill, P. T., Hernandez-Ortiz, J. P. & Graham, M. D. 2008 Diffusion and spatial correlations in suspensions of swimming particles. Phys. Rev. Lett. 100, 248101.Google Scholar
Zeff, B. W., Lanterman, D. D., McAllister, R., Roy, R., Kostelich, E. J. & Lathrop, D. P. 2003 Measuring intense rotation and dissipation in turbulent flows. Nature 421, 146–149.CrossRefGoogle ScholarPubMed
Zhan, C., Sardina, G., Lushi, E. & Brandt, L. 2013 Accumulation of motile elongated micro-organisms in turbulence. J. Fluid Mech. 739, 22–36.Google Scholar