Rotation of a superhydrophobic cylinder in a viscous liquid

Abstract

The hydrodynamic quantification of superhydrophobic slipperiness has traditionally employed two canonical problems – namely, shear flow about a single surface and pressure-driven channel flow. We here advocate the use of a new class of canonical problems, defined by the motion of a superhydrophobic particle through an otherwise quiescent liquid. In these problems the superhydrophobic effect is naturally measured by the enhancement of the Stokes mobility relative to the corresponding mobility of a homogeneous particle. We focus upon what may be the simplest problem in that class – the rotation of an infinite circular cylinder whose boundary is periodically decorated by a finite number of infinite grooves – with the goal of calculating the rotational mobility (velocity-to-torque ratio). The associated two-dimensional flow problem is defined by two geometric parameters – namely, the number 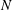$N$ of grooves and the solid fraction 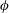$\unicode[STIX]{x1D719}$. Using matched asymptotic expansions we analyse the large-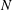$N$ limit, seeking the mobility enhancement from the respective homogeneous-cylinder mobility value. We thus find the two-term approximation,

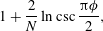$$\begin{eqnarray}\displaystyle 1+{\displaystyle \frac{2}{N}}\ln \csc {\displaystyle \frac{\unicode[STIX]{x03C0}\unicode[STIX]{x1D719}}{2}}, & & \displaystyle \nonumber\end{eqnarray}$$

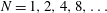for the ratio of the enhanced mobility to the homogeneous-cylinder mobility. Making use of conformal-mapping techniques and inductive arguments we prove that the preceding approximation is actually exact for $N=1,2,4,8,\ldots$. We conjecture that it is exact for all 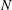$N$.