Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-01T03:49:00.875Z Has data issue: false hasContentIssue false
  • English
  • Français

The role of wake stiffness on the wake-induced vibration of the downstream cylinder of a tandem pair

Published online by Cambridge University Press:  08 February 2013

G. R. S. Assi ,
P. W. Bearman ,
B. S. Carmo ,
J. R. Meneghini ,
S. J. Sherwin  and
R. H. J. Willden
G. R. S. Assi
Affiliation:
Department of Naval Architecture and Ocean Engineering, University of São Paulo, São Paulo, 05508-030, Brazil
P. W. Bearman
Affiliation:
Department of Aeronautics, Imperial College, London SW7 2AZ, UK
B. S. Carmo
Affiliation:
Department of Mechanical Engineering, University of São Paulo, São Paulo, 05508-030, Brazil
J. R. Meneghini
Affiliation:
Department of Mechanical Engineering, University of São Paulo, São Paulo, 05508-030, Brazil
S. J. Sherwin
Affiliation:
Department of Aeronautics, Imperial College, London SW7 2AZ, UK
R. H. J. Willden
Affiliation:
Department of Engineering Science, University of Oxford, Oxford OX1 3PJ, UK
Get access Rights & Permissions [Opens in a new window]

Abstract

When a pair of tandem cylinders is immersed in a flow the downstream cylinder can be excited into wake-induced vibrations (WIV) due to the interaction with vortices coming from the upstream cylinder. Assi, Bearman & Meneghini (J. Fluid Mech., vol. 661, 2010, pp. 365–401) concluded that the WIV excitation mechanism has its origin in the unsteady vortex–structure interaction encountered by the cylinder as it oscillates across the wake. In the present paper we investigate how the cylinder responds to that excitation, characterising the amplitude and frequency of response and its dependency on other parameters of the system. 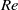We introduce the concept of wake stiffness, a fluid dynamic effect that can be associated, to a first approximation, with a linear spring with stiffness proportional to $\mathit{Re}$ and to the steady lift force occurring for staggered cylinders. By a series of experiments with a cylinder mounted on a base without springs we verify that such wake stiffness is not only strong enough to sustain oscillatory motion, but can also dominate over the structural stiffness of the system. We conclude that while unsteady vortex–structure interactions provide the energy input to sustain the vibrations, it is the wake stiffness phenomenon that defines the character of the WIV response.

JFM classification

Aerodynamics: Flow-structure interactions Wakes/Jets: Vortex streets Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 718 , 10 March 2013 , pp. 210 - 245
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Assi, G. R. S. 2009 Mechanisms for flow-induced vibration of interfering bluff bodies. PhD thesis, Imperial College London, London, UK. available from www.ndf.poli.usp.br/~gassi.Google Scholar
Assi, G. R. S., Bearman, P. W. & Meneghini, J. R. 2010 On the wake-induced vibration of tandem circular cylinders: the vortex interaction excitation mechanism. J. Fluid Mech. 661, 365–401.Google Scholar
Assi, G. R. S., Meneghini, J. R., Aranha, J. A. P., Bearman, P. W. & Casaprima, E. 2006 Experimental investigation of flow-induced vibration interference between two circular cylinders. J. Fluids Struct. 22, 819–827.CrossRefGoogle Scholar
Bearman, P. W. 1984 Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 16, 195–222.CrossRefGoogle Scholar
Blevins, R. D. 1990 Flow-Induced Vibration, 2nd edn. Van Nostrand Reinhold.Google Scholar
Bokaian, A. & Geoola, F. 1984 Wake-induced galloping of two interfering circular cylinders. J. Fluid Mech. 146, 383–415.CrossRefGoogle Scholar
Brika, D & Laneville, A. 1999 The flow interaction between a stationary cylinder and a downstream flexible cylinder. J. Fluids Struct. 13, 579–606.CrossRefGoogle Scholar
Govardhan, R. & Williamson, C. H. K. 2002 Resonance forever: existence of a critical mass and an infinite regime of resonance in vortex-induced vibration. J. Fluid Mech. 473, 147–166.CrossRefGoogle Scholar
Hover, F. S. & Triantafyllou, M. S. 2001 Galloping response of a cylinder with upstream wake interference. J. Fluids Struct. 15, 503–512.Google Scholar
Igarashi, T. 1981 Characteristics of the flow around two circular cylinders arranged in tandem. Bull. Japan Soc. Mech. Engrs 24, 323–331.Google Scholar
Khalak, A. & Williamson, C. H. K. 1999 Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13, 813–851.Google Scholar
King, R. & Johns, D. J. 1976 Wake interaction experiments with two flexible circular cylinders in flowing water. J. Sound Vib. 45, 259–283.CrossRefGoogle Scholar
Laneville, A. & Brika, D. 1999 The fluid and mechanical coupling between two circular cylinders in tandem arrangement. J. Fluids Struct. 13, 967–986.CrossRefGoogle Scholar
Morse, T. L. & Williamson, C. H. K. 2009 Prediction of vortex-induced vibration response by employing controlled motion. J. Fluid Mech. 634, 5–39.CrossRefGoogle Scholar
Norberg, C. 1998 LDV-measurements in the near wake of a circular cylinder. In Advances in Understanding of Bluff Body Wakes and Flow-Induced Vibration (ed. Williamson, C. H. K. & Bearman, P. W.). pp. 1–12. ASME.Google Scholar
Parkinson, G. V. 1989 Phenomena and modelling of flow-induced vibrations of bluff bodies. Prog. Aeronaut. Sci. 26, 169–224.Google Scholar
Price, S. J. 1975 Wake-induced flutter of power transmission conductors. J. Sound Vib. 38, 125–147.CrossRefGoogle Scholar
Price, S. J. 1976 The origin and nature of the lift force on the leeward of two bluff bodies. Aeronaut. Q. 26, 1154–1168.Google Scholar
Ruscheweyh, H. P. 1983 Aeroelastic interference effects between slender structures. J. Wind Engng Ind. Aerodyn. 14, 129–140.Google Scholar
Sarpkaya, T. 1979 Vortex-induced oscillations, a selective review. J. Appl. Mech. 46, 241–258.Google Scholar
Schaefer, J. W. & Eskinazi, S. 1958 An analysis of the vortex street generated in a viscous fluid. J. Fluid Mech. 6, 241–260.CrossRefGoogle Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.CrossRefGoogle Scholar
Zdravkovich, M. M. 1974 Flow-induced vibrations of two cylinders in tandem and their suppression. In International Symposium of Flow Induced Structural Vibrations (ed. Naudascher, E.). pp. 631–639. Springer.CrossRefGoogle Scholar
Zdravkovich, M. M. 1977 Review of flow interference between two circular cylinders in various arrangements. Trans. ASME: J. Fluids Engng 99, 618–633.Google Scholar
Zdravkovich, M. M. 1985 Flow induced oscillations of two interfering circular cylinders. J. Sound Vib. 101, 511–521.Google Scholar
Zdravkovich, M. M. 1988 Review of interference-induced oscillations in flow past two circular cylinders in various arrangements. J. Wind Engng Ind. Aerodyn. 28, 183–200.CrossRefGoogle Scholar
Zdravkovich, M. M. 1997 Flow Around Circular Cylinders, vol. 1. 1st edn. Oxford University Press.Google Scholar
Zdravkovich, M. M. & Medeiros, E. B. 1991 Effect of damping on interference-induced oscillations of two identical circular cylinders. J. Wind Engng Ind. Aerodyn. 38, 197–211.Google Scholar