Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-30T20:10:44.204Z Has data issue: false hasContentIssue false
  • English
  • Français

The role of surface charge convection in the electrohydrodynamics and breakup of prolate drops

Published online by Cambridge University Press:  02 November 2017

Rajarshi Sengupta ,
Lynn M. Walker  and
Aditya S. Khair Open the ORCID record for Aditya S. Khair [Opens in a new window]
Rajarshi Sengupta
Affiliation:
Department of Chemical Engineering, Carnegie Mellon University, Pittsburgh, PA 15213, USA
Lynn M. Walker
Affiliation:
Department of Chemical Engineering, Carnegie Mellon University, Pittsburgh, PA 15213, USA
Aditya S. Khair
Affiliation:
Department of Chemical Engineering, Carnegie Mellon University, Pittsburgh, PA 15213, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

The deformation of a weakly conducting, ‘leaky dielectric’, drop in a density matched, immiscible weakly conducting medium under a uniform direct current (DC) electric field is quantified computationally. We exclusively consider prolate drops, for which the drop elongates in the direction of the applied field. Furthermore, for the majority of this study, we assume the drop and medium to have equal viscosities. Using axisymmetric boundary integral computations, we delineate drop deformation and breakup regimes in the $Ca_{E}-Re_{E}$ parameter space, where 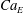$Ca_{E}$ is the electric capillary number (ratio of the electric to capillary stresses); and 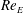$Re_{E}$ is the electric Reynolds number (ratio of charge relaxation to flow time scales), which characterizes the strength of surface charge convection along the interface. For so-called ‘prolate A’ drops, where the surface charge is convected towards the ‘poles’ of the drop, we demonstrate that increasing 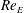$Re_{E}$ reduces the critical capillary number for breakup. Moreover, surface charge convection is the cause of an abrupt transition in the breakup mode of a drop from end pinching, where the drop elongates and develops bulbs at its ends that eventually detach, to a breakup mode characterized by the formation of conical ends. On the contrary, the deformation of ‘prolate B’ drops, where the surface charge is convected away from the poles, is essentially unaffected by the magnitude of 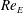$Re_{E}$.

JFM classification

Low-Reynolds-number flows: Boundary integral methods Drops and Bubbles: Drops and Bubbles Drops and Bubbles: Electrohydrodynamic effects
Type
Papers
Information
Journal of Fluid Mechanics , Volume 833 , 25 December 2017 , pp. 29 - 53
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ajayi, O. O. 1978 A note on Taylor’s electrohydrodynamic theory. Proc. R. Soc. Lond. A 364, 499–507.Google Scholar
Allan, R. S. & Mason, S. G. 1962 Particle behaviour in shear and electric fields. I. Deformation and burst of fluid drops. Proc. R. Soc. Lond. A 267, 45–61.Google Scholar
Basaran, O. A., Patzek, T. W., Brenner, R. E. Jr & Scriven, L. E. 1995 Nonlinear oscillations and breakup of conducting, inviscid drops in an externally applied electric field. Ind. Engng Chem. Res. 34, 3454–3465.Google Scholar
Baygents, J. C., Rivette, N. J. & Stone, H. A. 1990 Electrohydrodynamic deformation and interaction of drop pairs. J. Fluid Mech. 368, 359–375.Google Scholar
Baygents, J. C. & Saville, D. A. 1990 The circulation produced in a drop by an electric field: a high field strength electrokinetic model. In Drops and Bubbles: Third International Colloquium, vol. 197, pp. 7–17. AIP Conference Proceedings.Google Scholar
Collins, R. T., Jones, J. J., Harris, M. T. & Basaran, O. A. 2008 Electrohydrodynamic tip streaming and emission of charged drops from liquid cones. Nat. Phys. 4, 149–154.Google Scholar
Collins, R. T., Sambath, K., Harris, M. T. & Basaran, O. A. 2013 Universal scaling laws for the disintegration of electrified drops. Proc. Natl Acad. Sci. USA 110, 4905–4910.Google Scholar
Das, D. & Saintillan, D. 2016 A nonlinear small-deformation theory for transient droplet electrohydrodynamics. J. Fluid Mech. 810, 225–253.Google Scholar
Feng, J. Q. 1999 Electrohydrodynamic behaviour of a drop subjected to a steady uniform electric field at finite electric Reynolds number. Proc. R. Soc. Lond. A 455, 2245–2269.Google Scholar
Feng, J. Q. & Scott, T. C. 1996 A computational analysis of electrohydrodynamics of a leaky dielectric drop in an electric field. J. Fluid Mech. 311, 289–326.CrossRefGoogle Scholar
Fernandez, A. 2013 Modeling of electroconvective effects on the interaction between electric fields and low conductive drops. In ASME 2013 Fluids Engineering Division Summer Meeting, pp. V01CT25A004–V01CT25A004. American Society of Mechanical Engineers.Google Scholar
Gennari, O., Battista, L., Silva, B., Grilli, S., Miccio, L., Vespini, V., Coppola, S., Orlando, P., Aprin, L., Slangen, P. et al. 2015 Investigation on cone jetting regimes of liquid droplets subjected to pyroelectric fields induced by laser blasts. Appl. Phys. Lett. 106, 054103.Google Scholar
Ha, J. W. & Yang, S. M. 1995 Effects of surfactant on the deformation and stability of a drop in a viscous fluid in an electric field. J. Colloid Interface Sci. 175, 369–385.CrossRefGoogle Scholar
Ha, J. W. & Yang, S. M. 2000 Drop deformation and breakup of Newtonian and non-Newtonian conducting drops in an electric field. J. Fluid Mech. 405, 131–156.Google Scholar
Lac, E. & Homsy, G. M. 2007 Axisymmetric deformation and stability of a viscous drop in a steady electric field. J. Fluid Mech. 590, 239–264.Google Scholar
Lanauze, J. A.2016 Transient electrohydrodynamics of low-conductivity drops. PhD thesis, Carnegie Mellon University.Google Scholar
Lanauze, J. A., Walker, L. M. & Khair, A. S. 2013 The influence of inertia and charge relaxation on electrohydrodynamic drop deformation. Phys. Fluids 25, 112101.Google Scholar
Lanauze, J. A., Walker, L. M. & Khair, A. S. 2015 Nonlinear electrohydrodynamics of slightly deformed oblate drops. J. Fluid Mech. 774, 245–266.CrossRefGoogle Scholar
Macky, W. A. 1931 Some investigations on the deformation and breaking of water drops in strong electric fields. Proc. R. Soc. Lond. A 133, 565–587.Google Scholar
Melcher, J. R. & Taylor, G. I. 1969 Electrohydrodynamics: a review of the role of interfacial shear stresses. Annu. Rev. Fluid Mech. 1, 111–146.Google Scholar
Nganguia, H., Young, Y. N., Layton, A. T., Lai, M. C. & Hu, W. F. 2016 Electrohydrodynamics of a viscous drop with inertia. Phys. Rev. E 93, 053114.Google Scholar
O’Konski, C. T. & Thacher, H. C. Jr 1953 The distortion of aerosol droplets by an electric field. J. Phys. Chem. 57, 955–958.CrossRefGoogle Scholar
Pillai, R., Berry, J. D., Harvie, D. J. E. & Davidson, M. R. 2015 Electrolytic drops in an electric field: a numerical study of drop deformation and breakup. Phys. Rev. E 92, 013007.Google Scholar
Pillai, R., Berry, J. D., Harvie, D. J. E. & Davidson, M. R. 2016 Electrokinetics of isolated electrified drops. Soft Matt. 12, 3310–3325.CrossRefGoogle ScholarPubMed
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge University Press.Google Scholar
Pozrikidis, C. 2010 A Practical Guide to Boundary Element Methods with the Software Library BEMLIB. CRC Press.Google Scholar
Rallison, J. M. 1981 Numerical study of the deformation and burst of a viscous drop in general shear flows. J. Fluid Mech. 109, 465–482.Google Scholar
Salipante, P. F. & Vlahovska, P. M. 2010 Electrohydrodynamics of drops in strong uniform dc electric fields. Phys. Fluids 22, 112110.Google Scholar
Saville, D. A. 1997 Electrohydrodynamics: the Taylor–Melcher leaky dielectric model. Annu. Rev. Fluid Mech. 29, 27–64.CrossRefGoogle Scholar
Sherwood, J. D. 1988 Breakup of fluid droplets in electric and magnetic fields. J. Fluid Mech. 188, 133–146.CrossRefGoogle Scholar
Stone, H. A. & Leal, L. G. 1990 The effects of surfactants on drop deformation and breakup. J. Fluid Mech. 220, 161–186.CrossRefGoogle Scholar
Stone, H. A., Lister, J. A. & Brenner, M. P. 1999 Drops with conical ends in electric and magnetic fields. Proc. R. Soc. Lond. A 455, 329–347.Google Scholar
Supeene, G., Koch, C. R. & Bhattacharjee, S. 2008 Deformation of a droplet in an electric field: nonlinear transient response in perfect and leaky dielectric media. J. Colloid Interface Sci. 318, 436–476.CrossRefGoogle Scholar
Suvorov, V. G. & Litvinov, E. A. 2000 Dynamic Taylor cone formation on liquid metal surface: numerical modelling. J. Phys. D 33, 1245–1251.CrossRefGoogle Scholar
Taylor, G. I. 1964 Disintegration of water drops in an electric field. Proc. R. Soc. Lond. A 280, 383–397.Google Scholar
Taylor, G. I. 1966 Studies in electrohydrodynamics. I. The circulation produced in a drop by electrical field. Proc. R. Soc. Lond. A 291, 159–166.Google Scholar
Taylor, G. I. 1969 Electrically driven jets. Proc. R. Soc. Lond. A 313, 453–475.Google Scholar
Torza, S., Cox, R. G. & Mason, S. G. 1971 Electrohydrodynamic deformation and burst of liquid drops. Phil. Trans. R. Soc. Lond. A 269, 295–319.Google Scholar
Vizika, O. & Saville, D. A. 1992 The electrohydrodynamic deformation of drops suspended in liquids in steady and oscillatory electric fields. J. Fluid Mech. 239, 1–21.Google Scholar
Wilson, C. T. R. & Taylor, G. I. 1925 The bursting of soap-bubbles in a uniform electric field. Math. Proc. Cambridge Philos. Soc. 22, 728–730.Google Scholar
Yacubowicz, J. & Narkis, M. 1986 Dielectric behavior of carbon black filled polymer composites. Polym. Engng Sci. 26, 1568–1573.Google Scholar
Yariv, E. & Rhodes, D. 2013 Electrohydrodynamic drop deformation by strong electric fields: slender-body analysis. SIAM J. Appl. Maths 73, 2143–2161.CrossRefGoogle Scholar
Yezer, B. A., Khair, A. S., Sides, P. J. & Prieve, D. C. 2015 Use of electrochemical impedance spectroscopy to determine double-layer capacitance in doped nonpolar liquids. J. Colloid Interface Sci. 449, 2–12.CrossRefGoogle ScholarPubMed
Yezer, B. A., Khair, A. S., Sides, P. J. & Prieve, D. C. 2016 Determination of charge carrier concentration in doped nonpolar liquids by impedance spectroscopy in the presence of charge adsorption. J. Colloid Interface Sci. 469, 325–337.CrossRefGoogle ScholarPubMed
Youngren, G. K. & Acrivos, A. 1975 Stokes flow past a particle of arbitrary shape: a numerical method of solution. J. Fluid Mech. 69, 377–403.Google Scholar
Zeleny, J. 1917 Instability of electrified liquid surfaces. Phys. Rev. 10, 1.Google Scholar
Zubarev, N. M. 2001 Formation of conic cusps at the surface of liquid metal in electric field. JETP Lett. 73, 544–548.CrossRefGoogle Scholar
Zubarev, N. M. 2002 Self-similar solutions for conic cusps formation at the surface of dielectric liquids in electric field. Phy. Rev. E 65, 055301.Google Scholar