Article contents
The role of soluble surfactant in the linear instability of a film coating inside a tube
Published online by Cambridge University Press: 23 October 2023
Abstract
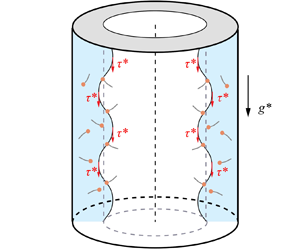
This study investigates the linear instability of a thin-film coating inside a rigid tube. The flow is assumed to be inertialess and driven by an axial body force (e.g. gravity), an interfacial shearing force, or their combinations. The interface and the bulk of the film are laden with soluble surfactant. The properties of the soluble surfactant, i.e. solubility, sorption kinetics and bulk diffusivity, modulate the interfacial dynamics of the film. The influence of these properties on the linear instability of the film is comprehensively investigated via long-wave approximation analysis and numerical calculation. Two modes, namely the interface mode and the surfactant mode, are identified to dominate the instability. For a quiescent film, it is found that solubility, sorption kinetics and bulk diffusivity act to improve the uniformity of the surface surfactant and mitigate the stabilizing effect of the Marangoni force. For the film driven by the axial body/interfacial shearing force, the results reveal that solubility plays contrasting roles in the interface mode and the surfactant mode. A window with intermediate solubility is detected where the film can be linearly stabilized. Moreover, sorption kinetics is found to destabilize the perturbations with long wavelength whereas it stabilizes the perturbations with finite wavelength. The bulk diffusivity of the surfactant has a non-monotonic influence on the flow instability, and the film can be relatively stable at both strong and weak diffusivity.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 1
- Cited by



