Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T12:54:01.408Z Has data issue: false hasContentIssue false
  • English
  • Français

Role of overturns in optimal mixing in stratified mixing layers

Published online by Cambridge University Press:  08 August 2017

A. Mashayek Open the ORCID record for A. Mashayek [Opens in a new window] ,
C. P. Caulfield Open the ORCID record for C. P. Caulfield [Opens in a new window]  and
W. R. Peltier
A. Mashayek*
Affiliation:
Department of Earth Atmosphere and Planetary Sciences, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
C. P. Caulfield
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
W. R. Peltier
Affiliation:
Department of Physics, University of Toronto, Ontario, M5S 1A7, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Turbulent mixing plays a major role in enabling the large-scale ocean circulation. The accuracy of mixing rates estimated from observations depends on our understanding of basic fluid mechanical processes underlying the nature of turbulence in a stratified fluid. Several of the key assumptions made in conventional mixing parameterizations have been increasingly scrutinized in recent years, primarily on the basis of adequately high resolution numerical simulations. We add to this evidence by compiling results from a suite of numerical simulations of the turbulence generated through stratified shear instability processes. We study the inherently intermittent and time-dependent nature of wave-induced turbulent life cycles and more specifically the tight coupling between inherently anisotropic scales upon which small-scale isotropic turbulence grows. The anisotropic scales stir and stretch fluid filaments enhancing irreversible diffusive mixing at smaller scales. We show that the characteristics of turbulent mixing depend on the relative time evolution of the Ozmidov length scale 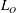$L_{O}$ compared to the so-called Thorpe overturning scale 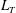$L_{T}$ which represents the scale containing available potential energy upon which turbulence feeds and grows. We find that when 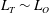$L_{T}\sim L_{O}$, the mixing is most active and efficient since stirring by the largest overturns becomes ‘optimal’ in the sense that it is not suppressed by ambient stratification. We argue that the high mixing efficiency associated with this phase, along with observations of 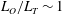$L_{O}/L_{T}\sim 1$ in oceanic turbulent patches, together point to the potential for systematically underestimating mixing in the ocean if the role of overturns is neglected. This neglect, arising through the assumption of a clear separation of scales between the background mean flow and small-scale quasi-isotropic turbulence, leads to the exclusion of an highly efficient mixing phase from conventional parameterizations of the vertical transport of density. Such an exclusion may well be significant if the mechanism of shear-induced turbulence is assumed to be representative of at least some turbulent events in the ocean. While our results are based upon simulations of shear instability, we show that they are potentially more generic by making direct comparisons with 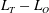$L_{T}-L_{O}$ data from ocean and lake observations which represent a much wider range of turbulence-inducing physical processes.

JFM classification

Turbulent Flows: Stratified turbulence Mixing: Turbulent mixing Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 522 - 552
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alford, M. H. & Pinkel, R. 2000 Observations of overturning in the thermocline: the context of ocean mixing. J. Phys. Oceanogr. 30 (5), 805–832.Google Scholar
Bartello, P. & Tobias, S. M. 2013 Sensitivity of stratified turbulence to the buoyancy Reynolds number. J. Fluid Mech. 725, 1–22.Google Scholar
Bouffard, D. & Boegman, L. 2013 A diapycnal diffusivity model for stratified environmental flows. Dyn. Atmos. Oceans 61–62, 14–34.Google Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J.-M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.Google Scholar
Caulfield, C. P. & Peltier, W. R. 1994 Three-dimensionalization of the stratified mixing layer. Phys. Fluids 6, 3803–3805.Google Scholar
Caulfield, C. P. & Peltier, W. R. 2000 Anatomy of the mixing transition in homogeneous and stratified free shear layers. J. Fluid Mech. 413, 1–47.Google Scholar
Crawford, W. R. 1986 A comparison of length scales and decay times of turbulence in stably stratified flows. J. Phys. Oceanogr. 16 (11), 1847–1854.Google Scholar
Dillon, T. M. 1982 Vertical overturns: a comparison of Thorpe and Ozmidov length scales. J. Geophys. Res. 87 (C12), 9601–9613.Google Scholar
Ferron, B., Mercier, H., Speer, K., Gargett, A. & Polzin, K. 1998 Mixing in the Romanche fracture zone. J. Phys. Oceanogr. 28 (10), 1929–1945.Google Scholar
Frants, M., Damerell, G. M., Gille, S. T., Heywood, K. J., MacKinnon, J. & Sprintall, J. 2013 An assessment of density-based finescale methods for estimating diapycnal diffusivity in the Southern Ocean. J. Atmos. Ocean. Technol. 30 (11), 2647–2661.Google Scholar
Fritts, D. C., Bizon, C., Werne, J. A. & Meyer, C. K. 2003 Layering accompanying turbulence generation due to shear instability and gravity-wave breaking. J. Geophys. Res. 108 (D8), 8452.Google Scholar
Gargett, A. E., Osborn, T. R. & Nasmyth, P. W. 1984 Local isotropy and the decay of turbulence in a stratified fluid. J. Fluid Mech. 144 (1), 231–280.Google Scholar
Garrett, C. 2003 Internal tides and ocean mixing. Science 301 (5641), 1858–1859.Google Scholar
Geyer, W. R., Lavery, A. C., Scully, M. E. & Trowbridge, J. H. 2010 Mixing by shear instability at high Reynolds number. Geophys. Res. Lett. 37, L22607.Google Scholar
Gibson, C. H. 1980 Fossil temperature, salinity, and vorticity turbulence in the ocean. Elsevier Oceanogr. Series 28, 221–257.Google Scholar
van Haren, H. & Gostiaux, L. 2010 A deep-ocean Kelvin–Helmholtz billow train. Geophys. Res. Lett. 37, L03605.Google Scholar
van Haren, H. & Gostiaux, L. 2012 Detailed internal wave mixing above a deep-ocean slope. J. Mar. Res. 70, 173–197.Google Scholar
Howard, L. N. 1961 Note on a paper of John W. Miles. J. Fluid Mech. 10, 509–512.Google Scholar
Itsweire, E. C., Koseff, J. R., Briggs, D. A. & Ferziger, J. H. 1993 Turbulence in stratified shear flows: implications for interpreting shear-induced mixing in the ocean. J. Phys. Oceanogr. 23 (7), 1508–1522.Google Scholar
Ivey, G. N. & Imberger, J. 1991 On the nature of turbulence in a stratified fluid. Part I: the energetics of mixing. J. Phys. Oceanogr. 21, 650–658.Google Scholar
Ivey, G. N., Winters, K. B. & Koseff, J. R. 2008 Density stratification, turbulence, but how much mixing? Annu. Rev. Fluid Mech. 40, 169–184.Google Scholar
Klaassen, G. P. & Peltier, W. R. 1985a The effect of Prandtl number on the evolution and stability of Kelvin–Helmholtz billows. Geophys. Astrophys. Fluid Dyn. 32, 23–60.Google Scholar
Klaassen, G. P. & Peltier, W. R. 1985b The onset of turbulence in finite amplitude Kelvin–Helmholtz billows. J. Fluid Mech. 155, 1–35.Google Scholar
Kunze, E. 2014 The relation between unstable shear layer thicknesses and turbulence lengthscales. J. Mar. Res. 72 (2), 95–104.Google Scholar
Kunze, E., Firing, E., Hummon, J. M., Chereskin, T. K. & Thurnherr, A. M. 2006 Global abyssal mixing inferred from lowered ADCP shear and CTD strain profiles. J. Phys. Oceanogr. 36 (8), 1553–1576.Google Scholar
Lien, R.-C., Caldwell, D. R., Gregg, M. C. & Moum, J. N. 1995 Turbulence variability at the equator in the central Pacific at the beginning of the 1991–1993 El Nino. J. Geophys. Res. 100 (C4), 6881–6898.Google Scholar
Mashayek, A.2013 Diapycnal mixing in the ocean: from dissipation scale to large scale meridional overturning circulation. PhD thesis, University of Toronto.Google Scholar
Mashayek, A., Caulfield, C. P. & Peltier, W. R. 2013 Time-dependent, non-monotonic mixing in stratified turbulent shear flows: implications for oceanographic estimates of buoyancy flux. J. Fluid Mech. 736, 570–593.Google Scholar
Mashayek, A. & Peltier, W. R. 2011 Turbulence transition in stratified atmospheric and oceanic shear flows: Reynolds and Prandtl number controls upon the mechanism. Geophys. Res. Lett. 38 (16), L16612.Google Scholar
Mashayek, A. & Peltier, W. R. 2012a The ‘zoo’ of secondary instabilities precursory to stratified shear flow transition. Part 1 shear aligned convection, pairing, and braid instabilities. J. Fluid Mech. 708, 5–44.Google Scholar
Mashayek, A. & Peltier, W. R. 2012b The ‘zoo’ of secondary instabilities precursory to stratified shear flow transition. Part 2 the influence of stratification. J. Fluid Mech. 708, 45–70.Google Scholar
Mashayek, A. & Peltier, W. R. 2013 Shear-induced mixing in geophysical flows: does the route to turbulence matter to its efficiency? J. Fluid Mech. 725, 216–261.Google Scholar
Mashayek, A., Salehipour, H., Bouffard, D., Caulfield, C. P., Ferrari, R., Nikurashin, M., Peltier, W. R. & Smyth, W. D. 2017 Efficiency of turbulent mixing in the abyssal ocean circulation. Geophys. Res. Lett. 44, 6296–6306.Google Scholar
Mater, B. D., Schaad, S. M. & Venayagamoorthy, S. K. 2013 Relevance of the Thorpe length scale in stably stratified turbulence. Phys. Fluids 25 (7), 076604.Google Scholar
Mater, B. D. & Venayagamoorthy, S. K. 2014 A unifying framework for parameterizing stably stratified shear-flow turbulence. Phys. Fluids 26 (3), 036601.Google Scholar
Mater, B. D., Venayagamoorthy, S. K., St. Laurent, L. & Moum, J. N. 2015 Biases in Thorpe scale estimates of turbulence dissipation Part I: assessments from large-scale overturns in oceanographic data. J. Phys. Oceanogr. 45 (10), 2497–2521.Google Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10, 496–508.Google Scholar
Moum, J. N. 1996 Energy-containing scales of turbulence in the ocean thermocline. J. Geophys. Res. 101 (C6), 14095–14109.Google Scholar
Nikurashin, M. & Ferrari, R. 2011 Global energy conversion rate from geostrophic flows into internal lee waves in the deep ocean. Geophys. Res. Lett. 38 (8), L08610.Google Scholar
Osborn, T. R. 1980 Estimates of the local rate of vertical diffusion from dissipation measurements. J. Phys. Oceanogr. 10, 83–89.Google Scholar
Osborn, T. R. & Cox, C. S. 1972 Oceanic fine structure. Geophys. Astrophys. Fluid Dyn. 3 (1), 321–345.Google Scholar
Peltier, W. R. & Caulfield, C. P. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35, 135–167.Google Scholar
Pham, H. T. & Sarkar, S. 2010 Transport and mixing of density in a continuously stratified shear layer. J. Turb. 24, 1–23.Google Scholar
Potylitsin, P. G. & Peltier, W. R. 1998 Stratification effects on the stability of columnar vortices on the f-plane. J. Fluid Mech. 355, 45–79.Google Scholar
Potylitsin, P. G. & Peltier, W. R. 1999 Three-dimensional destabilization of Stuart vortices: the influence of rotation and ellipticity. J. Fluid Mech. 387, 205–226.Google Scholar
Rahmani, M., Lawrence, G. A. & Seymour, B. R. 2014 The effect of Reynolds number on mixing in Kelvin–Helmholtz billows. J. Fluid Mech. 759, 612–641.Google Scholar
Salehipour, H., Caulfield, C. P. & Peltier, W. R. 2016a Turbulent mixing due to the Holmboe wave instability at high Reynolds number. J. Fluid Mech. 803, 591–621.Google Scholar
Salehipour, H. & Peltier, W. R. 2015 Diapycnal diffusivity, turbulent Prandtl number and mixing efficiency in boussinesq stratified turbulence. J. Fluid Mech. 775, 464–500.Google Scholar
Salehipour, H., Peltier, W. R. & Mashayek, A. 2015 Turbulent diapycnal mixing in stratified shear flows: the influence of Prandtl number on mixing efficiency and transition at high Reynolds number. J. Fluid Mech. 773, 178–223.Google Scholar
Salehipour, H., Peltier, W. R., Whalen, C. B. & MacKinnon, J. A. 2016b A new characterization of the turbulent diapycnal diffusivities of mass and momentum in the ocean. Geophys. Res. Lett. 43, 3370–3379.Google Scholar
Scotti, A. 2015 Biases in Thorpe scale estimates of turbulence dissipation Part II: energetics arguments and turbulence simulations. J. Phys. Oceanogr. 45 (10), 2522–2543.Google Scholar
Smyth, W. D., Moum, J. & Caldwell, D. 2001 The efficiency of mixing in turbulent patches: inferences from direct simulations and microstructure observations. J. Phys. Oceanogr. 31, 1969–1992.Google Scholar
Smyth, W. D. & Moum, J. N. 2000a Length scales of turbulence in stably stratified mixing layers. Phys. Fluids 12, 1327–1342; herein SM00.Google Scholar
Smyth, W. D. & Moum, J. N. 2000b Anisotropy of turbulence in stably stratified mixing layers. Phys. Fluids 12, 1343–1362.Google Scholar
Smyth, W. D. & Moum, J. N. 2001 Three-dimensional turbulence. In Encyclopedia of Ocean Sciences, vol. 6, pp. 2947–2955. Academic.Google Scholar
Smyth, W. D. & Moum, J. N. 2012 Ocean mixing by Kelvin–Helmholtz instability. Oceanography 25, 140–149.Google Scholar
Smyth, W. D. & Moum, J. N 2013 Marginal instability and deep cycle turbulence in the eastern equatorial Pacific ocean. Geophys. Res. Lett. 40, 6181–6185.Google Scholar
Smyth, W. D. & Peltier, W. R. 1994 Three-dimensionalization of barotropic vortices on the f-plane. J. Fluid Mech. 265, 25–64.Google Scholar
St. Laurent, L. & Simmons, H. 2006 Estimates of power consumed by mixing in the ocean interior. J. Clim. 19, 4877–4890.Google Scholar
Thorpe, S. A. 1977 Turbulence and mixing in a Scottish loch. Phil. Trans. R. Soc. Lond. A 286 (1334), 125–181.Google Scholar
Thorpe, S. A. 2005 The Turbulent Ocean. Cambridge University Press.Google Scholar
Van Haren, H., Gostiaux, L., Morozov, E. & Tarakanov, R. 2014 Extremely long Kelvin–Helmholtz billow trains in the Romanche Fracture zone. Geophys. Res. Lett. 41, 8445–8451.Google Scholar
Voet, G., Girton, J. B., Alford, M. H., Carter, G. S., Klymak, J. M. & Mickett, J. B. 2015 Pathways, volume transport, and mixing of abyssal water in the samoan passage. J. Phys. Oceanogr. 45 (2), 562–588.Google Scholar
Waterhouse, A. F., Mackinnon, J. A., Nash, J. D., Alford, M. H., Kunze, E., Simmons, H. L., Polzin, K. L., St Laurent, L. C., Sun, O., Pinkel, R. et al. 2014 Global patterns of diapycnal mixing from measurements of the turbulent dissipation rate. J. Phys. Oceanogr. 44 (7), 1854–1872.Google Scholar
Wijesekera, H. W & Dillon, T. M. 1997 Shannon entropy as an indicator of age for turbulent overturns in the oceanic thermocline. J. Geophys. Res. 102 (C2), 3279–3291.Google Scholar
Winters, K., Lombard, P., Riley, J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.Google Scholar
Woods, A. W., Caulfield, C. P., Landel, J. R. & Kuesters, A. 2010 Non-invasive turbulent mixing across a density interface in a turbulent Taylor–Couette flow. J. Fluid Mech. 663, 343–347.Google Scholar
Wunsch, C. & Ferrari, R. 2004 Vertical mixing, energy, and the general circulation of the oceans. Annu. Rev. Fluid Mech. 36, 281–314.Google Scholar