Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-12-01T03:55:54.779Z Has data issue: false hasContentIssue false
  • English
  • Français

Rogue wave occurrence and dynamics by direct simulations of nonlinear wave-field evolution

Published online by Cambridge University Press:  27 February 2013

Wenting Xiao ,
Yuming Liu ,
Guangyu Wu  and
Dick K. P. Yue
Wenting Xiao
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Yuming Liu
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Guangyu Wu
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Dick K. P. Yue*
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the occurrence and dynamics of rogue waves in three-dimensional deep water using phase-resolved numerical simulations based on a high-order spectral (HOS) method. We obtain a large ensemble of nonlinear wave-field simulations (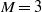$M= 3$ in HOS method), initialized by spectral parameters over a broad range, from which nonlinear wave statistics and rogue wave occurrence are investigated. The HOS results are compared to those from the broad-band modified nonlinear Schrödinger (BMNLS) equations. Our results show that for (initially) narrow-band and narrow directional spreading wave fields, modulational instability develops, resulting in non-Gaussian statistics and a probability of rogue wave occurrence that is an order of magnitude higher than linear theory prediction. For longer times, the evolution becomes quasi-stationary with non-Gaussian statistics, a result not predicted by the BMNLS equations (without consideration of dissipation). When waves spread broadly in frequency and direction, the modulational instability effect is reduced, and the statistics and rogue wave probability are qualitatively similar to those from linear theory. To account for the effects of directional spreading on modulational instability, we propose a new modified Benjamin–Feir index for effectively predicting rogue wave occurrence in directional seas. For short-crested seas, the probability of rogue waves based on number frequency is imprecise and problematic. We introduce an area-based probability, which is well defined and convergent for all directional spreading. Based on a large catalogue of simulated rogue wave events, we analyse their geometry using proper orthogonal decomposition (POD). We find that rogue wave profiles containing a single wave can generally be described by a small number of POD modes.

JFM classification

Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 720 , 10 April 2013 , pp. 357 - 392
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Chevron Energy Technology Company, 1400 Smith Street, Houston, TX 77002, USA.

References

Abdalla, S. & Cavaleri, L. 2002 Effect of wind variability and variable air density on wave modelling. J. Geophys. Res. 107 (C7), 3080.Google Scholar
Alber, I. E. 1978 The effects of randomness on the stability of two-dimensional surface wavetrains. Proc. R. Soc. Lond. A. 363, 525–546.Google Scholar
Annenkov, S. Y. & Shrira, V. I. 2009a Evolution of kurtosis for wind waves. Geophys. Res. Lett. 36, L13603.Google Scholar
Annenkov, S. Y & Shrira, V. I. 2009b Fast nonlinear evolution in wave turbulence. Phys. Rev. Lett. 102 (2), 24502.Google Scholar
Bateman, W. J. D., Swan, C. & Taylor, P. H. 2001 On the efficient numerical simulation of directionally spread surface water waves. J. Comput. Phys. 174 (1), 277–305.Google Scholar
Benjamin, T. B. & Feir, J. E. 1967 The disintegration of wave trains in deep water. Part 1. Theory. J. Fluid Mech. 27 (3), 417–430.CrossRefGoogle Scholar
Boccotti, P. 1983 Some new results on statistical properties of wind waves. Appl. Ocean Res. 5 (3), 134–140.Google Scholar
Chalikov, D. 2009 Freak waves: their occurrence and probability. Phys. Fluids 21, 076602.Google Scholar
Clamond, D., Francius, M., Grue, J. & Kharif, C. 2006 Long time interaction of envelope solitons and freak wave formations. Eur. J. Mech. (B/Fluids) 25, 536–553.CrossRefGoogle Scholar
Dommermuth, D. 2000 The initialization of nonlinear waves using an adjustment scheme. Wave Motion 32 (4), 307–317.Google Scholar
Dommermuth, D. & Yue, D. K. P. 1987 A higher-order spectral method for the study of nonlinear gravity waves. J. Fluid Mech. 184, 267–288.CrossRefGoogle Scholar
Dommermuth, D. & Yue, D. K. P. 1988 The nonlinear three-dimensional waves generated by a moving surface disturbance. In Proceedings of 17th Symposium on Naval Hydrodynamics, The Hague, The Netherlands.Google Scholar
Dysthe, K. B. 1979 Note on a modification to the nonlinear Schrödinger equation for application to deep water waves. Proc. R. Soc. Lond. A 369 (1736), 105–114.Google Scholar
Dysthe, K. B., Krogstad, H. E. & Muller, P. 2008 Oceanic rogue waves. Annu. Rev. Fluid Mech. 40, 287–310.Google Scholar
Dysthe, K. B., Trulsen, K., Krogstad, H. E. & Socquet-Juglard, H. 2003 Evolution of a narrow-band spectrum of random surface gravity waves. J. Fluid Mech. 478, 1–10.CrossRefGoogle Scholar
Forristall, G. Z. 2000 Wave crest distributions: observations and second-order theory. J. Phys. Oceanogr. 30 (8), 1931–1943.Google Scholar
Forristall, G. Z. 2005 Understanding rogue waves: are new physics really necessary? In Rogue Waves: Proceedings of the 14th ‘Aha Huliko‘a Hawaiian Winter Workshop, Honolulu, HI, pp. 29–35.Google Scholar
Gemmrich, J. R. & Farmer, D. M. 1999 Observations of the scale and occurrence of breaking surface waves. J. Phys. Oceanogr. 29 (10), 2595–2606.2.0.CO;2>CrossRefGoogle Scholar
Gramstad, O. & Trulsen, K. 2007 Influence of crest and group length on the occurrence of freak waves. J. Fluid Mech. 582, 463–472.CrossRefGoogle Scholar
Guedes Soares, C., Cherneva, Z. & Antão, E. M. 2003 Characteristics of abnormal waves in North Sea storm sea states. Appl. Ocean Res. 25 (6), 337–344.Google Scholar
Hwang, P. A., Wang, D. W., Walsh, E. J., Krabill, W. B. & Swift, R. N. 2000 Airborne measurements of the wavenumber spectra of ocean surface waves. Part II: directional distribution. J. Phys. Oceanogr. 30 (11), 2768–2787.Google Scholar
Janssen, P. A. E. M. 2003 Nonlinear four-wave interactions and freak waves. J. Phys. Oceanogr. 33 (4), 863–884.2.0.CO;2>CrossRefGoogle Scholar
Janssen, P. A. E. M. 2009 On some consequences of the canonical transformation in the Hamiltonian theory of water waves. J. Fluid Mech. 637, 1–44.CrossRefGoogle Scholar
Kharif, C., Giovanangeli, J. P., Touboul, J., Grare, L. & Pelinovsky, E. 2007 Influence of wind on extreme wave events: experimental and numerical approaches. J. Fluid Mech. 594, 209–247.CrossRefGoogle Scholar
Kharif, C. & Pelinovsky, E. 2003 Physical mechanisms of the rogue wave phenomenon. Eur. J. Mech. (B/Fluids) 22 (6), 603–634.CrossRefGoogle Scholar
Kharif, C., Pelinovsky, E. & Slunyaev, A. 2009 Rogue Waves in the Ocean. Springer.Google Scholar
Lavrenov, I. V. 1998 The wave energy concentration at the Agulhas Current off South Africa. Natural Hazards 17 (2), 117–127.Google Scholar
Lawton, G. 2001 Monsters of the deep (the perfect wave). New Sci. 170 (2297), 28–32.Google Scholar
Lindgren, G. 1970 Some properties of a normal process near a local maximum. Ann. Math. Statist. 41 (6), 1870–1883.CrossRefGoogle Scholar
Liu, Y. & Yue, D. K. P. 1998 On generalized Bragg scattering of surface waves by bottom ripples. J. Fluid Mech. 356, 297–326.CrossRefGoogle Scholar
Lo, E. & Mei, C. C. 1985 A numerical study of water-wave modulation based on a higher-order nonlinear Schrödinger equation. J. Fluid Mech. 150, 395–416.CrossRefGoogle Scholar
Longuet-Higgins, M. S. 1952 On the statistical distribution of the heights of sea waves. J. Mar. Res. 11 (3), 245–266.Google Scholar
Longuet-Higgins, M. S. 1963 The effect of nonlinearities on statistical distribution in the theory of sea waves. J. Fluid Mech. 17, 459–480.Google Scholar
McLean, J. W. 1982 Instabilities of finite-amplitude gravity waves on water of finite depth. J. Fluid Mech. 114, 331–341.CrossRefGoogle Scholar
Mori, N. & Janssen, P. A. E. M. 2006 On kurtosis and occurrence probability of freak waves. J. Phys. Oceanogr. 36 (7), 1471–1483.CrossRefGoogle Scholar
Mori, N., Onorato, M. & Janssen, P. A. E. M. 2011 On the estimation of the kurtosis in directional sea states for freak wave forecasting. J. Phys. Oceanogr. 41 (8), 1484–1497.CrossRefGoogle Scholar
Mori, N. & Yasuda, T. 2002 A weakly non-Gaussian model of wave height distribution for random wave train. Ocean Engng 29 (10), 1219–1231.CrossRefGoogle Scholar
Onorato, M., Cavaleri, L., Fouques, S., Gramstad, O., Janssen, P. A. E. M., Monbaliu, J., Osborne, A. R., Pakozdi, C., Serio, M., Stansberg, C. T., Toffoli, A. & Trulsen, K. 2009 Statistical properties of mechanically generated surface gravity waves: a laboratory experiment in a three-dimensional wave basin. J. Fluid Mech. 627, 235–257.CrossRefGoogle Scholar
Onorato, M., Cavaleri, L., Gramstad, O., Janssen, P. A. E. M., Monbaliu, J., Osborne, A. R., Serio, M., Stansberg, C. T., Toffoli, A. & Trulsen, K. 2008 Statistical properties of mechanically generated surface gravity waves: a laboratory experiment in a 3D wave basin. In Rogue Waves 2008, Brest, France.Google Scholar
Onorato, M., Osborne, A. R. & Serio, M. 2002 Extreme wave events in directional, random oceanic sea states. Phys. Fluids 14 (4), L25–L28.CrossRefGoogle Scholar
Onorato, M., Osborne, A. R., Serio, M. & Bertone, S. 2001 Freak waves in random oceanic sea states. Phys. Rev. Lett. 86 (25), 5831–5834.Google Scholar
Onorato, M., Osborne, A. R., Serio, M., Cavaleri, L., Brandini, C. & Stansberg, C. T. 2004 Observation of strongly non-Gaussian statistics for random sea surface gravity waves in wave flume experiments. Phys. Rev. E 70 (6), 067302.Google Scholar
Pinho, U. F., Liu, P. C. & Ribeira, C. E. P. 2004 Freak waves at Campos Basin, Brazil. Geofizika 21, 53–66.Google Scholar
Piterbarg, V. I. 1996 Asymptotic Methods in the Theory of Gaussian Processes and Fields, Translations of Mathematical Monographs, vol. 148. American Mathematical Society.Google Scholar
Rapp, R. J. & Melville, W. K. 1990 Laboratory measurements of deep-water breaking waves. Phil. Trans. R. Soc. Lond. A 331 (1622), 735–800.Google Scholar
Ruban, V. P. 2011 Enhanced rise of rogue waves in slant wave groups. JETP Lett. 94 (3), 177–181.Google Scholar
Segur, H., Henderson, D., Carter, J., Hammack, J., Li, C.-M., Pheiff, D. & Socha, K. 2005 Stabilizing the Benjamin–Feir instability. J. Fluid Mech. 539, 229–271.CrossRefGoogle Scholar
Shemer, L., Kit, E. & Jiao, H. 2002 An experimental and numerical study of the spatial evolution of unidirectional nonlinear water-wave groups. Phys. Fluids 14, 3380.Google Scholar
Shemer, L. & Sergeeva, A. 2009 An experimental study of spatial evolution of statistical parameters in a unidirectional narrow-banded random wavefield. J. Geophys. Res. 114 (C1), C01015.Google Scholar
Shemer, L., Sergeeva, A. & Liberzon, D. 2010a Effect of the initial spectrum on the spatial evolution of statistics of unidirectional nonlinear random waves. J. Geophys. Res. 115 (C12), C12039.Google Scholar
Shemer, L., Sergeeva, A. & Slunyaev, A. 2010b Applicability of envelope model equations for simulation of narrow-spectrum unidirectional random wave field evolution: experimental validation. Phys. Fluids 22, 016601.CrossRefGoogle Scholar
Skourup, J., Hansen, N. E. O. & Andreasen, K. K. 1997 Non-Gaussian extreme waves in the central North Sea. J. Offshore Mech. Arctic Engng 119 (3), 146–150.Google Scholar
Slunyaev, A., Didenkulova, I. & Pelinovsky, E. 2011 Rogue waters. Contemp. Phys. 52 (6), 571–590.Google Scholar
Slunyaev, A. V. & Sergeeva, A. V. 2011 Stochastic simulation of unidirectional intense waves in deep water applied to rogue waves. JETP Lett. 94 (10), 779–786.Google Scholar
Socquet-Juglard, H., Dysthe, K., Trulsen, K., Krogstad, H. E. & Liu, J. 2005 Probability distributions of surface gravity waves during spectral changes. J. Fluid Mech. 542, 195–216.Google Scholar
Stansberg, C. T. 1994 Effects from directionality and spectral bandwidth on nonlinear spatial modulations of deep-water surface gravity wave trains. In Proceedings of the 24th International Conference on Coastal Engineering, Kobe, Japan, vol. 1, pp. 579–593. ASCE.Google Scholar
Stansell, P. 2005 Distributions of extreme wave, crest and trough heights measured in the North Sea. Ocean Engng 32 (8–9), 1015–1036.CrossRefGoogle Scholar
Stocker, J. R. & Peregrine, D. H. 1999 The current-modified nonlinear Schrödinger equation. J. Fluid Mech. 399, 335–353.CrossRefGoogle Scholar
Tayfun, M. A. 1980 Narrow-band nonlinear sea waves. J. Geophys. Res. 85 (C3), 1548–1552.Google Scholar
Toffoli, A., Cavaleri, L., Babanin, A. V., Benoit, M., Bitner-Gregersen, E. M., Monbaliu, J., Onorato, M., Osborne, A. R. & Stansberg, C. T. 2011 Occurrence of extreme waves in three-dimensional mechanically generated wave fields propagating over an oblique current. Nat. Hazards Earth Syst. Sci. 11, 895–903.Google Scholar
Toffoli, A., Gramstad, O., Trulsen, K., Monbaliu, J., Bitner-Gregersen, E. & Onorato, M. 2010 Evolution of weakly nonlinear random directional waves: laboratory experiments and numerical simulations. J. Fluid Mech. 664, 313–336.CrossRefGoogle Scholar
Toffoli, A., Lefevre, J. M., Bitner-Gregersen, E. & Monbaliu, J. 2005 Towards the identification of warning criteria: analysis of a ship accident database. Appl. Ocean Res. 27 (6), 281–291.Google Scholar
Trulsen, K. & Dysthe, K. B. 1996 A modified nonlinear Schrödinger equation for broader bandwidth gravity waves on deep water. Wave Motion 24, 281–289.CrossRefGoogle Scholar
Waseda, T., Kinoshita, T. & Tamura, H. 2009 Evolution of a random directional wave and freak wave occurrence. J. Phys. Oceanogr. 39 (3), 621–639.Google Scholar
West, B. J., Brueckner, K. A., Janda, R. S., Milder, D. M. & Milton, R. L. 1987 A new numerical method for surface hydrodynamics. J. Geophys. Res. 92 (C11), 11803–11824.CrossRefGoogle Scholar
Wu, G. 2004 Direct simulation and deterministic prediction of large-scale nonlinear ocean wave-field. PhD thesis, Massachusetts Institute of Technology, Cambridge, MA.Google Scholar
Wu, G., Liu, Y. & Yue, D. K. P. 2006 A note on stabilizing the Benjamin–Feir instability. J. Fluid Mech. 556, 45–54.Google Scholar
Xiao, W. 2013 Study of directional ocean wavefield evolution and rogue wave occurrence using large-scale phase-resolved nonlinear simulations. PhD thesis, Massachusetts Institute of Technology, Cambridge, MA.Google Scholar
Zakharov, V. E., Dyachenko, A. I. & Vasilyev, O. A. 2002 New method for numerical simulation of a nonstationary potential flow of incompressible fluid with a free surface. Eur. J. Mech. (B/Fluids) 21 (3), 283–291.CrossRefGoogle Scholar