Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-24T13:29:10.115Z Has data issue: false hasContentIssue false
  • English
  • Français

Robust features of a turbulent boundary layer subjected to high-intensity free-stream turbulence

Published online by Cambridge University Press:  20 July 2018

R. Jason Hearst Open the ORCID record for R. Jason Hearst [Opens in a new window] ,
Eda Dogan  and
Bharathram Ganapathisubramani
R. Jason Hearst*
Affiliation:
Department of Energy and Process Engineering, Norwegian University of Science and Technology, Trondheim, NO-7491, Norway Engineering and the Environment, University of Southampton, SouthamptonSO17 1BJ, UK
Eda Dogan
Affiliation:
Linné FLOW Centre, KTH Mechanics, Stockholm, SE-10044, Sweden Engineering and the Environment, University of Southampton, SouthamptonSO17 1BJ, UK
Bharathram Ganapathisubramani
Affiliation:
Engineering and the Environment, University of Southampton, SouthamptonSO17 1BJ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The influence of the large scale organisation of free-stream turbulence on a turbulent boundary layer is investigated experimentally in a wind tunnel through hot-wire measurements. An active grid is used to generate high-intensity free-stream turbulence with turbulence intensities and local turbulent Reynolds numbers in the ranges 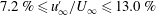$7.2\,\%\leqslant u_{\infty }^{\prime }/U_{\infty }\leqslant 13.0\,\%$ and 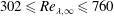$302\leqslant Re_{\unicode[STIX]{x1D706},\infty }\leqslant 760$, respectively. In particular, several cases are produced with fixed 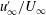$u_{\infty }^{\prime }/U_{\infty }$ and 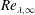$Re_{\unicode[STIX]{x1D706},\infty }$, but up to a 65 % change in the free-stream integral scale 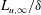$L_{u,\infty }/\unicode[STIX]{x1D6FF}$. It is shown that, while qualitatively the spectra at various wall-normal positions in the boundary layer look similar, there are quantifiable differences at the large wavelengths all the way to the wall. Nonetheless, profiles of the longitudinal statistics up to fourth order are well collapsed between cases at the same 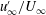$u_{\infty }^{\prime }/U_{\infty }$. It is argued that a larger separation of the integral scale would not yield a different result, nor would it be physically realisable. Comparing cases across the wide range of turbulence intensities and free-stream Reynolds numbers tested, it is demonstrated that the near-wall spectral peak is independent of the free-stream turbulence, and seemingly universal. The outer peak was also found to be described by a set of global scaling laws, and hence both the near-wall and outer spectral peaks can be predicted a priori with only knowledge of the free-stream spectrum, the boundary layer thickness (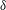$\unicode[STIX]{x1D6FF}$) and the friction velocity (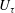$U_{\unicode[STIX]{x1D70F}}$). Finally, a conceptual model is suggested that attributes the increase in 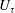$U_{\unicode[STIX]{x1D70F}}$ as 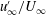$u_{\infty }^{\prime }/U_{\infty }$ increases to the build-up of energy at large wavelengths near the wall because that energy cannot be transferred to the universal near-wall spectral peak.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 851 , 25 September 2018 , pp. 416 - 435
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baars, W. J., Hutchins, N. & Marusic, I. 2016 Spectral stochastic estimation of high-Reynolds-number wall-bounded turbulence for a refined inner–outer interaction model. Phys. Rev. F 1, 054406.Google Scholar
Brandt, L., Schlatter, P. & Henningson, D. S. 2004 Transition in boundary layers subject to free-stream turbulence. J. Fluid Mech. 517, 167–198.Google Scholar
Castro, I. P. 1984 Effects of free stream turbulence on low Reynolds number boundary layers. J. Fluids Engng 106 (3), 298–306.Google Scholar
Corrsin, S. 1963 Turbulence: experimental methods. In Handbuch der Physik (ed. Flügge, S. & Truesdell, C. A.), pp. 524–589. Springer.Google Scholar
Dogan, E., Hanson, R. & Ganapathisubramani, B. 2016 Interactions of large-scale free-stream turbulence with turbulent boundary layers. J. Fluid Mech. 802, 79–107.Google Scholar
Dogan, E., Hearst, R. J. & Ganapathisubramani, B. 2017 Modelling high Reynolds number wall–turbulence interactions in laboratory experiments using large-scale free-stream turbulence. Phil. Trans. R. Soc. A 375 (2089), 20160091.Google Scholar
Ertunç, Ö., Özyilmaz, N., Lienhart, H., Durst, F. & Beronov, K. 2010 Homogeneity of turbulence generated by static-grid structures. J. Fluid Mech. 654, 473–500.Google Scholar
Esteban, L. B., Dogan, E., Rodríguez-López, E. & Ganapathisubramani, B. 2017 Skin-friction measurements in a turbulent boundary layer under the influence of free-stream turbulence. Exp. Fluids 58 (9), 115.Google Scholar
Fransson, J. H. M., Matsubara, M. & Alfredsson, P. H. 2005 Transition induced by free-stream turbulence. J. Fluid Mech. 527, 1–25.Google Scholar
Hack, M. J. P. & Zaki, T. A. 2014 Streak instabilities in boundary layers beneath free-stream turbulence. J. Fluid Mech. 741, 280–315.Google Scholar
Hancock, P. E. & Bradshaw, P. 1983 The effect of free-stream turbulence on turbulent boundary layers. J. Fluids Engng 105, 284–289.Google Scholar
Hancock, P. E. & Bradshaw, P. 1989 Turbulence structure of a boundary layer beneath a turbulent free stream. J. Fluid Mech. 205, 45–76.Google Scholar
Hearst, R. J., Buxton, O. R. H., Ganapathisubramani, B. & Lavoie, P. 2012 Experimental estimation of fluctuating velocity and scalar gradients in turbulence. Exp. Fluids 53 (4), 925–942.Google Scholar
Hearst, R. J., Gomit, G. & Ganapathisubramani, B. 2016 Effect of turbulence on the wake of a wall-mounted cube. J. Fluid Mech. 804, 513–530.Google Scholar
Hearst, R. J. & Lavoie, P. 2014 Decay of turbulence generated by a square-fractal-element grid. J. Fluid Mech. 741, 567–584.Google Scholar
Hearst, R. J. & Lavoie, P. 2015 The effect of active grid initial conditions on high Reynolds number turbulence. Exp. Fluids 56 (10), 185.Google Scholar
Hearst, R. J. & Lavoie, P. 2016 Effects of multi-scale and regular grid geometries on decaying turbulence. J. Fluid Mech. 803, 528–555.Google Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. A 365, 657–664.Google Scholar
Isaza, J. C., Salazar, R. & Warhaft, Z. 2014 On grid-generated turbulence in the near- and far field regions. J. Fluid Mech. 753, 402–426.Google Scholar
Kang, H. S., Chester, S. & Meneveau, C. 2003 Decaying turbulence in an active-grid-generated flow and comparisons with large-eddy simulation. J. Fluid Mech. 480, 129–160.Google Scholar
Klewicki, J. C. 2010 Reynolds number dependence, scaling, and dynamics of turbulent boundary layers. J. Fluids Engng 132, 094001.Google Scholar
Klewicki, J., Fife, P. & Wei, T. 2009 On the logarithmic mean profile. J. Fluid Mech. 638, 73–93.Google Scholar
Klewicki, J., Fife, P., Wei, T. & McMurtry, P. 2007 A physical model of the turbulent boundary layer consonant with mean momentum balance structure. Phil. Trans. R. Soc. A 365, 823–839.Google Scholar
Kreilos, T., Khapko, T., Schlatter, P., Duguet, Y., Henningson, D. S. & Eckhardt, B. 2016 Bypass transition and spot nucleation in boundary layers. Phys. Rev. F 1, 043602.Google Scholar
Larssen, J. V. & Devenport, W. J. 2011 On the generation of large-scale homogeneous turbulence. Exp. Fluids 50, 1207–1223.Google Scholar
Makita, H. 1991 Realization of a large-scale turbulence field in a small wind tunnel. Fluid Dyn. Res. 8, 53–64.Google Scholar
Marusic, I., Baars, W. J. & Hutchins, N. 2017 Scaling of the streamwise turbulence intensity in the context of inner–outer interactions in wall turbulence. Phys. Rev. F 2, 100502.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Mydlarski, L. & Warhaft, Z. 1996 On the onset of high-Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331–368.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S. & Chong, M. S. 2005 Evidence of the k 1 -1 law in a high-Reynolds-number turbulent boundary layer. Phys. Rev. Lett. 95, 074501.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S., Hutchins, N. & Chong, M. S. 2007 Some predictions of the attached eddy model for a high Reynolds number boundary layer. Phil. Trans. R. Soc.  A 365, 807–822.Google Scholar
Rodríguez-López, E., Bruce, P. J. K. & Buxton, O. R. H. 2015 A robust post-processing method to determine skin friction in turbulent boundary layers from the velocity profile. Exp. Fluids 56 (4), 68.Google Scholar
Schlatter, P. & Örlü, R. 2012 Turbulent boundary layers at moderate Reynolds numbers: inflow length and tripping effects. J. Fluid Mech. 710, 5–34.Google Scholar
Shahinfar, S. & Fransson, J. H. M. 2011 Effect of free-stream turbulence characteristics on boundary layer transition. J. Phys.: Conf. Ser. 318, 032019.Google Scholar
Sharp, N., Neuscamman, S. & Warhaft, Z. 2009 Effects of large-scale free stream turbulence on a turbulent boundary layer. Phys. Fluids 21, 095105.Google Scholar
Smits, A. J., Monty, J. P., Hultmark, M., Bailey, S. C. C., Hutchins, N. & Marusic, I. 2011 Spatial resolution correction for wall-bounded turbulence measurements. J. Fluid Mech. 676, 41–53.Google Scholar
Thormann, A. & Meneveau, C. 2014 Decay of homogeneous, nearly isotropic turbulence behind active fractal grids. Phys. Fluids 26, 025112.Google Scholar
Valente, P. C. & Vassilicos, J. C. 2012 Universal dissipation scaling for nonequilibrium turbulence. Phys. Rev. Lett. 108, 214503.Google Scholar
Vassilicos, J. C. 2015 Dissipation in turbulent flows. Annu. Rev. Fluid Mech. 47, 95–114.Google Scholar
Vincenti, P., Klewicki, J., Morrill-Winter, C., White, C. M. & Wosnik, M. 2013 Streamwise velocity statistics in turbulent boundary layers that spatially develop to high Reynolds number. Exp. Fluids 54, 1629.Google Scholar
Wu, X., Moin, P., Wallace, J. M., Skarda, J., Lozano-Durán, A. & Hickey, J.-P. 2017 Transitional–turbulent spots and turbulent–turbulent spots in boundary layers. Proc. Natl Acad. Sci. USA 114 (27), E5292–E5299.Google Scholar