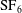Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-08T04:27:47.476Z Has data issue: false hasContentIssue false
  • English
  • Français

The Richtmyer–Meshkov instability of a ‘V’ shaped air/$\text{SF}_{6}$ interface

Published online by Cambridge University Press:  03 August 2016

Xisheng Luo ,
Ping Dong ,
Ting Si  and
Zhigang Zhai
Xisheng Luo
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Ping Dong
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Ting Si
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Zhigang Zhai*
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The Richtmyer–Meshkov instability on a ‘V’ shaped air/SF$_{6}$ gaseous interface is experimentally studied in a shock tube. By the soap film technique, a discontinuous interface without supporting mesh is formed so that the initial conditions of the interface can be accurately controlled. Five ‘V’ shaped air/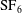$\text{SF}_{6}$ interfaces with different vertex angles (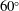$60^{\circ }$, 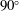$90^{\circ }$, 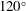$120^{\circ }$, 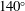$140^{\circ }$ and 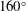$160^{\circ }$) are created where the ratio of the initial interface amplitude to the wavelength varies to highlight the effects of initial condition on the flow characteristics. The wave patterns and interface morphologies are clearly identified in the high-speed schlieren sequences, which show that the interface deforms in a less pronounced manner with less vortices generated as the vertex angle increases. A regime change is observed in the interface width growth rate near a vertex angle of 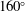$160^{\circ }$, which provides an experimental evidence for the numerical results obtained by McFarland et al. (Phys. Scr. vol. T155, 2013, 014014). The growth rate of interface width in the linear phase is compared with the theoretical predictions from the classical impulsive model and a modified linear model, and the latter is proven to be effective for a moderate to large initial amplitude. It is found that the initial growth rate of the interface width is a non-monotone function of the initial vertex angle (amplitude–wavelength ratio), i.e. the interface width growth rate in the linear stage experiences an increase and then a decrease as the vertex angle increases. A similar conclusion was also reached by Dell et al. (Phys. Plasmas, vol. 22, 2015, 092711) numerically for a sinusoidal interface. Finally, the general behaviour of the interface width growth in the nonlinear stage can be well captured by the nonlinear model proposed by Dimonte & Ramaprabhu (Phys. Fluids, vol. 22, 2010, 014104).

JFM classification

Compressible Flows: Compressible Flows Mixing: Mixing Compressible Flows: Shock waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 802 , 10 September 2016 , pp. 186 - 202
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abd-el Fattah, A. M. & Henderson, L. F. 1978a Shock waves at a fast-slow gas interface. J. Fluid Mech. 86, 15–32.CrossRefGoogle Scholar
Abd-el Fattah, A. M. & Henderson, L. F. 1978b Shock waves at a slow-fast gas interface. J. Fluid Mech. 89, 79–95.CrossRefGoogle Scholar
Baker, G. R., Meiron, D. I. & Orszag, S. A. 1980 Vortex simulations of the Rayleigh–Taylor instability. Phys. Fluids 23, 1485–1491.CrossRefGoogle Scholar
Bakhrakh, S. M., Klopov, B. A., Meshkov, E. E., Tolshmyakov, A. I. & Yanilkin, Y. V. 1995 Development of perturbations of a shock-accelerated interface between two gases. J. Appl. Mech. Tech. Phy. 36, 341–346.CrossRefGoogle Scholar
Balakumar, B. J., Orlicz, G. C., Ristorcelli, J. R., Balasubramanian, S., Prestridge, K. P. & Tomkins, C. D. 2012 Turbulent mixing in a Richtmyer–Meshkov fluid layer after reshock: velocity and density statistics. J. Fluid Mech. 696, 67–93.CrossRefGoogle Scholar
Bashurov, V. V., Bondarenko, Y. A., Gubkov, E. V., Dudin, V. I., Meshkov, E. E., Poduvalov, A. N., Shanin, A. A., Stenin, A. M., Til’kunov, V. A., Tolshmyakov, A. I. et al. 1997 Experimental and numerical evolution studies for 2D perturbations of the interface accelerated by shock waves. Laser Part. Beams 15, 101–114.CrossRefGoogle Scholar
Bonazza, R. & Sturtevant, B. 1996 X-ray measurements of growth rates at a gas interface accelerated by shock waves. Phys. Fluids 8, 2496–2512.CrossRefGoogle Scholar
Brouillette, M. 2002 The Richtmyer–Meshkov instability. Annu. Rev. Fluid Mech. 34, 445–468.CrossRefGoogle Scholar
Buttler, W. T., Oró, D. M., Preston, D. L., Mikaelian, K. O., Cherne, F. J., Hixson, R. S., Mariam, F. G., Morris, C., Stone, J. B., Terrones, G. & Tupa, D. 2012 Unstable Richtmyer–Meshkov growth of solid and liquid metals in vacuum. J. Fluid Mech. 703, 60–84.CrossRefGoogle Scholar
Dell, Z., Stellingwerf, R. F. & Abarzhi, S. I. 2015 Effect of initial perturbation amplitude on Richtmyer–Meshkov flows induced by strong shocks. Phys. Plasmas 22, 092711.CrossRefGoogle Scholar
Dimonte, G. & Ramaprabhu, P. 2010 Simulations and model of the nonlinear Richtmyer–Meshkov instability. Phys. Fluids 22, 014104.CrossRefGoogle Scholar
Haehn, N., Weber, C., Oakley, J. G., Anderson, M. H., Ranjan, D. & Bonazza, R. 2011 Experimental investigation of a twice-shocked spherical gas inhomogeneity with particle image velocimetry. Shock Waves 21, 225–231.CrossRefGoogle Scholar
Hahn, M., Drikakis, D., Youngs, D. L. & Williams, R. J. R. 2011 Richtmyer–Meshkov turbulent mixing arising from an inclined material interface with realistic surface perturbations and reshocked flow. Phys. Fluids 23, 046101.CrossRefGoogle Scholar
Hawley, J. F. & Zabusky, N. J. 1989 Vortex paradigm for shock-accelerated density-stratified interfaces. Phys. Rev. Lett. 63, 1241–1244.CrossRefGoogle ScholarPubMed
Holder, D. A. & Barton, C. J. 2004 Shock tube Richtmyer–Meshkov experiments: inverse chevron and half height. In Proceedings of the Ninth International Workshop on the Physics of Compressible Turbulent Mixing (ed. Dalziel, S. B.), Cambridge, UK.Google Scholar
Isenberg, C. 1992 The Science of Soap Films and Soap Bubbles. Dover.Google Scholar
Jacobs, J. W. 1992 Shock-induced mixing of a light-gas cylinder. J. Fluid Mech. 234, 629–649.CrossRefGoogle Scholar
Jahn, R. G. 1956 The refraction of shock waves at a gaseous interface. J. Fluid Mech. 1, 457–489.CrossRefGoogle Scholar
Jones, M. A. & Jacobs, J. W. 1997 A membraneless experiment for the study of Richtmyer–Meshkov instability of a shock-accelerated gas interface. Phys. Fluids 9, 3078–3085.CrossRefGoogle Scholar
Lindl, J. D., Landen, O., Edwards, J., Moses, E. & NIC Team 2014 Review of the national ignition campaign 2009–2012. Phys. Plasmas 21, 020501.CrossRefGoogle Scholar
Luo, X., Guan, B., Si, T. & Zhai, Z. 2016 Richtmyer–Meshkov instability of a three-dimensional SF6 -air interface with a minimum-surface feature. Phys. Rev. E 93, 013101.Google Scholar
Luo, X., Wang, X. & Si, T. 2013 The Richtmyer–Meshkov instability of a three-dimensional air/SF6 interface with a minimum-surface feature. J. Fluid Mech. 722, R2.CrossRefGoogle Scholar
Luo, X., Wang, M., Si, T. & Zhai, Z. 2015 On the interaction of a planar shock with an SF6 polygon. J. Fluid Mech. 773, 366–394.CrossRefGoogle Scholar
Mcfarland, J. A., Greenough, J. A. & Ranjan, D. 2011 Computational parametric study of a Richtmyer–Meshkov instability for an inclined interface. Phys. Rev. E 84, 026303.Google ScholarPubMed
Mcfarland, J. A., Greenough, J. A. & Ranjan, D. 2013 Investigation of the initial perturbation amplitude for the inclined interface Richtmyer–Meshkov instability. Phys. Scr. T155, 014014.CrossRefGoogle Scholar
Mcfarland, J. A., Greenough, J. A. & Ranjan, D. 2014a Simulations and analysis of the reshocked inclined interface Richtmyer–Meshkov instability for linear and nonlinear interface perturbations. Trans. ASME 136, 071203.Google Scholar
Mcfarland, J. A., Reilly, D., Black, W., Greenough, J. A. & Ranjan, D. 2015 Modal interactions between a large-wavelength inclined interface and small-wavelength multimode perturbations in a Richtmyer–Meshkov instability. Phys. Rev. E 92, 013023.Google Scholar
Mcfarland, J. A., Reilly, D., Creel, S., Mcdonald, C., Finn, T. & Ranjan, D. 2014b Experimental investigation of the inclined interface Richtmyer–Meshkov instability before and after reshock. Exp. Fluids 55, 1640–1653.CrossRefGoogle Scholar
Meshkov, E. E. 1969 Instability of the interface of two gases accelerated by a shock wave. Fluid Dyn. 4, 101–104.CrossRefGoogle Scholar
Mikaelian, K. O. 1993 Functions sin k x and cos k x. J. Phys. A: Math. Gen. 26, 1673–1689.CrossRefGoogle Scholar
Mikaelian, K. O. 2005 Richtmyer–Meshkov instability of arbitrary shapes. Phys. Fluids 17, 034101.CrossRefGoogle Scholar
Morgan, R., Aure, R., Stockero, J., Greenough, J., Cabot, W., Likhachev, O. & Jacobs, J. 2012 On the late-time growth of the two-dimensional Richtmyer–Meshkov instability in shock tube experiments. J. Fluid Mech. 712, 354–383.CrossRefGoogle Scholar
Motl, B., Oakley, J., Ranjan, D., Weber, C., Anderson, M. & Bonazza, R. 2009 Experimental validation of a Richtmyer–Meshkov scaling law over large density ratio and shock strength ranges. Phys. Fluids 21, 126102.CrossRefGoogle Scholar
Ranjan, D., Oakley, J. & Bonazza, R. 2011 Shock-bubble interactions. Annu. Rev. Fluid Mech. 43, 117–140.CrossRefGoogle Scholar
Reilly, D., Mcfarland, J. A., Mohaghar, M. & Ranjan, D. 2015 The effects of initial conditions and circulation deposition on the inclined-interface reshocked Richtmyer–Meshkov instability. Exp. Fluids 56, 168–183.CrossRefGoogle Scholar
Richtmyer, R. D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Maths 13, 297–319.CrossRefGoogle Scholar
Rikanati, A., Oron, D., Sadot, O. & Shvarts, D. 2003 High initial amplitude and high Mach number effects on the evolution of the single-mode Richtmyer–Meshkov instability. Phys. Rev. E 67, 026307.Google ScholarPubMed
Samtaney, R. 2003 Suppression of the Richtmyer–Meshkov instability in the presence of a magnetic field. Phys. Fluids 15, L53–L56.CrossRefGoogle Scholar
Samtaney, R. & Pullin, D. I. 1996 On initial-value and self-similar solutions of the compressible Euler equations. Phys. Fluids 8, 2650–2655.CrossRefGoogle Scholar
Samtaney, R., Ray, J. & Zabusky, N. 1998 Baroclinic circulation generation on shock accelerated slow/fast gas interfaces. Phys. Fluids 10, 1217–1230.CrossRefGoogle Scholar
Samtaney, R. & Zabusky, N. J. 1994 Circulation deposition on shock-accelerated planar and curved density-stratified interfaces: models and scalling laws. J. Fluid Mech. 269, 45–78.CrossRefGoogle Scholar
Si, T., Long, T., Zhai, Z. & Luo, X. 2015 Experimental investigation of cylindrical converging shock waves interacting with a polygonal heavy gas cylinder. J. Fluid Mech. 784, 225–251.CrossRefGoogle Scholar
Tomkins, C. D., Balakumar, B. J., Orlicz, G. C., Prestridge, K. P. & Ristorcelli, J. R. 2013 Evolution of the density self-correlation in developing Richtmyer–Meshkov turbulence. J. Fluid Mech. 735, 288–306.CrossRefGoogle Scholar
Velikovich, A. L. & Dimonte, G. 1996 Nonlinear perturbation theory of the incompressible Richtmyer–Meshkov instability. Phys. Rev. Lett. 76 (17), 3112–3115.Google ScholarPubMed
Wang, M., Si, T. & Luo, X. 2013 Generation of polygonal gas interfaces by soap film for Richtmyer–Meshkov instability study. Exp. Fluids 54, 1427–1435.CrossRefGoogle Scholar
Wang, T., Liu, J. H., Bai, J. S., Jiang, Y., Li, P. & Liu, K. 2012 Experimental and numerical investigation of inclined air/SF6 interface instability under shock wave. Z. Angew. Math. Mech. Appl. Math. Mech. 33, 37–50.CrossRefGoogle Scholar
Yang, J., Kubota, T. & Zukoski, E. E. 1994 A model for characterization of a vortex pair formed by shock passage over a light-gas inhomogeneity. J. Fluid Mech. 258, 217–244.CrossRefGoogle Scholar
Zabusky, N. 1999 Vortex paradigm for accelerated inhomogeneous flows: visiometrics for the Rayleigh–Taylor and Richtmyer–Meshkov environments. Annu. Rev. Fluid Mech. 31, 495–536.CrossRefGoogle Scholar
Zhai, Z., Si, T., Luo, X. & Yang, J. 2011 On the evolution of spherical gas interfaces accelerated by a planar shock wave. Phys. Fluids 23, 084104.CrossRefGoogle Scholar
Zhai, Z., Wang, M., Si, T. & Luo, X. 2014a On the interaction of a planar shock with a light polygonal interface. J. Fluid Mech. 757, 800–816.CrossRefGoogle Scholar
Zhai, Z., Zhang, F., Si, T. & Luo, X. 2014b Evolution of heavy gas cylinder under reshock conditions. J. Vis. 17, 123–129.CrossRefGoogle Scholar