Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-12-01T02:46:01.642Z Has data issue: false hasContentIssue false
  • English
  • Français

Rheology of vesicle suspensions under combined steady and oscillating shear flows

Published online by Cambridge University Press:  30 April 2012

A. Farutin  and
C. Misbah
A. Farutin*
Affiliation:
Université Grenoble 1/CNRS, Laboratoire Interdisciplinaire de Physique/UMR5588, Grenoble F-38041, France
C. Misbah
Affiliation:
Université Grenoble 1/CNRS, Laboratoire Interdisciplinaire de Physique/UMR5588, Grenoble F-38041, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Viscoelastic properties of complex fluids are usually extracted by applying an oscillatory shear rat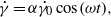e ( where 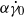is a constant which is small for a linear response to make sense) to the fluid. This leads to a complex effective viscosity where its real part carries information on viscous effects while its imaginary part informs us on elastic properties. We show here theoretically, by taking a dilute vesicle suspension as an example, that application of a pure shearing oscillation misses several interesting microscopic features of the suspension. It is shown that if, in addition to the oscillatory part, a basic constant shear rate is applied to the suspension (so that the total shear rate is 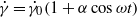, with 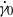a constant), then the complex viscosity reveals much more insightful properties of the suspension. First, it is found that the complex viscosity exhibits a resonance for tank-treading vesicles as a function of the frequency of oscillation. This resonance is linked to the fact that vesicles, while being in the stable tank-treading regime (with their main axis having a steady orientation with respect to the flow direction), possess damped oscillatory modes. Second, in the region of parameter space where the vesicle exhibits either vacillating-breathing (permanent oscillations of the main axis about the flow direction and breathing of the shape) or tumbling modes, the complex viscosity shows an infinite number of resonances as a function of the frequency. It is shown that these behaviours markedly differ from that obtained when only the classical oscillation 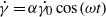is applied. The results are obtained numerically by solution of the analytical constitutive equation of a dilute vesicle suspension and confirmed analytically by a linear-response phenomenological theory. It is argued that the same type of behaviour is expected for any suspension of soft entities (capsules, red blood cells, etc.) that exhibit periodic motion under constant shear flow. We shall also discuss the reason why this type of behaviour could not have been captured by existing constitutive laws of complex fluids.

JFM classification

Biological Fluid Dynamics: Capsule/cell dynamics Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 700 , 10 June 2012 , pp. 362 - 381
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bagchi, P. & Kalluri, R. M. 2009 Dynamics of nonspherical capsules in shear flow. Phys. Rev. E 80 (1), 016307.CrossRefGoogle ScholarPubMed
2. Bagchi, P. & Kalluri, R. M. 2011 Dynamic rheology of a dilute suspension of elastic capsules: effect of capsule tank-treading, swinging and tumbling. J. Fluid Mech. 669, 498–526.CrossRefGoogle Scholar
3. Barthès-Biesel, D. 2009 Capsule motion in flow: Deformation and membrane buckling. Comptes Rendus Physique 10 (8), 764–774.CrossRefGoogle Scholar
4. Batchelor, G. K. 1970 The stress system in a suspension of force-free particles. J. Fluid Mech. 41 (03), 545–570.CrossRefGoogle Scholar
5. Biben, T., Farutin, A. & Misbah, C. 2011 Three-dimensional vesicles under shear flow: Numerical study of dynamics and phase diagram. Phys. Rev. E 83 (3), 031921.CrossRefGoogle ScholarPubMed
6. Bird, R. B., Armstrong, R. C. & Hassager, O. 1987 Dynamics of Polymeric Liquids, 2nd edn. Fluid Dynamics , vol. 1. Wiley.Google Scholar
7. Booij, H. C. 1966a Influence of superimposed steady shear flow on the dynamic properties of non-Newtonian fluids. I. Measurements on non-Newtonian solutions. Rheol. Acta 5, 215–221.CrossRefGoogle Scholar
8. Booij, H. C. 1966b Influence of superimposed steady shear flow on the dynamic properties of non-Newtonian fluids. II. Theoretical approach based on the Oldroyd theory. Rheol. Acta 5, 222–227.CrossRefGoogle Scholar
9. Clausen, J. R. & Aidun, C. K. 2010 Capsule dynamics and rheology in shear flow: Particle pressure and normal stress. Phys. Fluids 22 (12), 123302.CrossRefGoogle Scholar
10. Cox, R. G. 1969 The deformation of a drop in a general time-dependent fluid flow. J. Fluid Mech. 37 (03), 601–623.CrossRefGoogle Scholar
11. Danker, G., Biben, T., Podgorski, T., Verdier, C. & Misbah, C. 2007 Dynamics and rheology of a dilute suspension of vesicles: Higher-order theory. Phys. Rev. E 76 (4), 041905.CrossRefGoogle ScholarPubMed
12. Danker, G. & Misbah, C. 2007 Rheology of a dilute suspension of vesicles. Phys. Rev. Lett. 98 (8), 088104.CrossRefGoogle ScholarPubMed
13. Deschamps, J., Kantsler, V. & Steinberg, V. 2009 Phase diagram of single vesicle dynamical states in shear flow. Phys. Rev. Lett. 102 (11), 118105.CrossRefGoogle ScholarPubMed
14. Farutin, A., Biben, T. & Misbah, C. 2010 Analytical progress in the theory of vesicles under linear flow. Phys. Rev. E 81 (6), 061904.CrossRefGoogle ScholarPubMed
15. Frankel, N. A. & Acrivos, A. 1970 The constitutive equation for a dilute emulsion. J. Fluid Mech. 44 (01), 65–78.CrossRefGoogle Scholar
16. Ghigliotti, G., Biben, T. & Misbah, C. 2010 Rheology of a dilute two-dimensional suspension of vesicles. J. Fluid Mech. 653, 489–518.CrossRefGoogle Scholar
17. Kantsler, V., Segre, E. & Steinberg, V. 2008 Dynamics of interacting vesicles and rheology of vesicle suspension in shear flow. Europhys. Lett. 82 (5), 58005.CrossRefGoogle Scholar
18. Kantsler, V. & Steinberg, V. 2006 Transition to tumbling and two regimes of tumbling motion of a vesicle in shear flow. Phys. Rev. Lett. 96, 036001.CrossRefGoogle ScholarPubMed
19. Larson, R. G. 1999 The Structure and Rheology of Complex Fluids. Oxford University Press.Google Scholar
20. Lebedev, V. V., Turitsyn, K. S. & Vergeles, S. S. 2007 Dynamics of nearly spherical vesicles in an external flow. Phys. Rev. Lett. 99 (21), 218101.CrossRefGoogle Scholar
21. Lebedev, V. V, Turitsyn, K. S & Vergeles, S. S 2008 Nearly spherical vesicles in an external flow. New J. Phys. 10 (4), 043044.CrossRefGoogle Scholar
22. Misbah, C. 2006 Vacillating breathing and tumbling of vesicles under shear flow. Phys. Rev. Lett. 96 (2), 028104.CrossRefGoogle ScholarPubMed
23. Noguchi, H. & Gompper, G. 2007 Swinging and tumbling of fluid vesicles in shear flow. Phys. Rev. Lett. 98 (12), 128103.CrossRefGoogle ScholarPubMed
24. Tirtaatmadja, V., Tam, K. C. & Jenkins, R. D. 1997 Superposition of oscillations on steady shear flow as a technique for investigating the structure of associative polymers. Macromolecules 30 (5), 1426–1433.CrossRefGoogle Scholar
25. Vergeles, S. 2008 Rheological properties of a vesicle suspension. JETP Lett 87, 511–515.CrossRefGoogle Scholar
26. Vitkova, V., Mader, M.-A., Polack, B., Misbah, C. & Podgorski, T. 2008 Micro-macro link in rheology of erythrocyte and vesicle suspensions. Biophys. J 95 (6), L33–L35.CrossRefGoogle ScholarPubMed
27. Vlahovska, P. M. & Gracia, R. S. 2007 Dynamics of a viscous vesicle in linear flows. Phys. Rev. E 75 (1), 016313.CrossRefGoogle ScholarPubMed
28. Vlahovska, P. M., Podgorski, T. & Misbah, C. 2009 Vesicles and red blood cells in flow: From individual dynamics to rheology. Comptes Rendus Physique 10 (8), 775–789.CrossRefGoogle Scholar
29. Vlastos, G., Lerche, D., Koch, B., Samba, O. & Pohl, M. 1997 The effect of parallel combined steady and oscillatory shear flows on blood and polymer solutions. Rheol. Acta 36, 160–172.CrossRefGoogle Scholar
30. Yazdani, A. Z. K., Kalluri, R. M. & Bagchi, P. 2011 Tank-treading and tumbling frequencies of capsules and red blood cells. Phys. Rev. E 83 (4), 046305.CrossRefGoogle ScholarPubMed
31. Zhao, H. & Shaqfeh, E. S. G. 2011 The dynamics of a vesicle in simple shear flow. J. Fluid Mech. 674, 578–604.CrossRefGoogle Scholar