Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-12T05:19:36.184Z Has data issue: false hasContentIssue false
  • English
  • Français

Rheology of sheared suspensions of rough frictional particles

Published online by Cambridge University Press:  23 September 2014

Stany Gallier ,
Elisabeth Lemaire ,
François Peters  and
Laurent Lobry
Stany Gallier*
Affiliation:
SAFRAN-Herakles, Le Bouchet Research Center, 91710 Vert le Petit, France Laboratory of Condensed Matter Physics (LPMC, UMR 6622), University of Nice, Parc Valrose, 06108 Nice, France
Elisabeth Lemaire
Affiliation:
Laboratory of Condensed Matter Physics (LPMC, UMR 6622), University of Nice, Parc Valrose, 06108 Nice, France
François Peters
Affiliation:
Laboratory of Condensed Matter Physics (LPMC, UMR 6622), University of Nice, Parc Valrose, 06108 Nice, France
Laurent Lobry
Affiliation:
Laboratory of Condensed Matter Physics (LPMC, UMR 6622), University of Nice, Parc Valrose, 06108 Nice, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper presents three-dimensional numerical simulations of non-Brownian concentrated suspensions in a Couette flow at zero Reynolds number using a fictitious domain method. Contacts between particles are modelled using a discrete element method (DEM)-like approach, which allows for a more physical description, including roughness and friction. This work emphasizes the effect of friction between particles and its role on rheological properties, especially on normal stress differences. 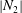Friction is shown to notably increase viscosity and second normal stress difference $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}|N_2|$ and decrease 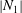$|N_1|$, in better agreement with experiments. The hydrodynamic and contact contributions to the overall particle stress are particularly investigated. This shows that the effect of friction is mostly due to the additional contact stress since the hydrodynamic stress remains unaffected by friction. Simulation results are also compared with experiments, such as normal stresses or effective friction coefficient 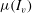$\mu (I_v)$, and the agreement is improved when friction is accounted for. This suggests that friction is operative in actual suspensions.

JFM classification

Complex Fluids: Complex Fluids Non-Newtonian Flows: Rheology Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 757 , 25 October 2014 , pp. 514 - 549
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. & Green, J. T. 1972 The hydrodynamic interaction of two small freely-moving spheres in a linear flow field. J. Fluid Mech. 56 (02), 375–400.Google Scholar
Blanc, F.2011 Rhéologie et microstructure des suspensions concentrées non-browniennes. PhD thesis, Université de Nice-Sophia Antipolis.Google Scholar
Blanc, F., Peters, F. & Lemaire, E. 2011 Experimental signature of the pair trajectories of rough spheres in the shear-induced microstructure in noncolloidal suspensions. Phys. Rev. Lett. 107 (20), 208302.Google Scholar
Bossis, G. & Brady, J. F. 1984 Dynamic simulation of sheared suspensions. I. General method. J. Chem. Phys. 80, 5141–5154.Google Scholar
Boyer, F., Guazzelli, E. & Pouliquen, O. 2011a Unifying suspension and granular rheology. Phys. Rev. Lett. 107 (18), 188301.Google Scholar
Boyer, F., Pouliquen, O. & Guazzelli, E. 2011b Dense suspensions in rotating-rod flows: normal stresses and particle migration. J. Fluid Mech. 686, 5–25.Google Scholar
Brady, J. F. & Bossis, G. 1985 The rheology of concentrated suspensions of spheres in simple shear flow by numerical simulation. J. Fluid Mech. 155, 105–129.Google Scholar
Brady, J. F. & Bossis, G. 1988 Stokesian dynamics. Annu. Rev. Fluid Mech. 20 (1), 111–157.Google Scholar
Brady, J. F. & Morris, J. F. 1997 Microstructure of strongly sheared suspensions and its impact on rheology and diffusion. J. Fluid Mech. 348, 103–139.Google Scholar
Chorin, A. J. 1968 Numerical solution of the Navier–Stokes equations. Maths Comput. 22 (104), 745–762.CrossRefGoogle Scholar
Coussot, P. & Ancey, C. 1999 Rheophysical classification of concentrated suspensions and granular pastes. Phys. Rev. E 59 (4), 4445–4457.Google Scholar
Couturier, É., Boyer, F., Pouliquen, O. & Guazzelli, É. 2011 Suspensions in a tilted trough: second normal stress difference. J. Fluid Mech. 10, 26–39.Google Scholar
DaCunha, F. R. & Hinch, E. J. 1996 Shear-induced dispersion in a dilute suspension of rough spheres. J. Fluid Mech. 309, 211–223.Google Scholar
Dai, S., Bertevas, E., Qi, F. & Tanner, R. 2013 Viscometric functions for noncolloidal sphere suspensions with Newtonian matrices. J. Rheol. 57 (2), 493–510.Google Scholar
Davis, R. H., Zhao, Y., Galvin, K. P. & Wilson, H. J. 2003 Solid–solid contacts due to surface roughness and their effects on suspension behaviour. Phil. Trans. R. Soc. Lond. A 361 (1806), 871–894.Google Scholar
Dbouk, T., Lobry, L. & Lemaire, E. 2013 Normal stresses in concentrated non-Brownian suspensions. J. Fluid Mech. 715, 239–272.Google Scholar
Drazer, G., Koplik, J., Khusid, B. & Acrivos, A. 2002 Deterministic and stochastic behaviour of non-Brownian spheres in sheared suspensions. J. Fluid Mech. 460 (1), 307–335.CrossRefGoogle Scholar
Drazer, G., Koplik, J., Khusid, B. & Acrivos, A. 2004 Microstructure and velocity fluctuations in sheared suspensions. J. Fluid Mech. 511, 237–263.CrossRefGoogle Scholar
Durlofsky, L., Brady, J. F. & Bossis, G. 1987 Dynamic simulation of hydrodynamically interacting particles. J. Fluid Mech. 180, 21–49.CrossRefGoogle Scholar
Gallier, S., Lemaire, E., Lobry, L. & Peters, F. 2014 A fictitious domain approach for the simulation of dense suspensions. J. Comput. Phys. 256, 367–387.CrossRefGoogle Scholar
Garland, S., Gauthier, G., Martin, J. & Morris, J. F. 2012 Normal stress measurements in sheared non-Brownian suspensions. J. Rheol. 57 (1), 71–88.CrossRefGoogle Scholar
Glowinski, R., Pan, T. W., Hesla, T. I., Joseph, D. D. & Periaux, J. 2001 A fictitious domain approach to the direct numerical simulation of incompressible viscous flow past moving rigid bodies: application to particulate flow. J. Comput. Phys. 169 (2), 363–426.CrossRefGoogle Scholar
Glowinski, R., Pan, T. W. & Periaux, J. 1998 Distributed Lagrange multiplier methods for incompressible viscous flow around moving rigid bodies. Comput. Meth. Appl. Mech. Engng 151 (1–2), 181–194.Google Scholar
Jeffrey, D. J., Morris, J. F. & Brady, J. F. 1993 The pressure moments for two rigid spheres in low-Reynolds-number flow. Phys. Fluids A 5 (10), 2317–2325.Google Scholar
Kim, S. & Karrila, S. J. 1991 Microhydrodynamics: Principles and Selected Applications, vol. 507. Butterworth-Heinemann.Google Scholar
Kromkamp, J., van den Ende, D., Kandhai, D., van der Sman, R. & Boom, R. 2006 Lattice Boltzmann simulation of 2D and 3D non-Brownian suspensions in Couette flow. Chem. Engng Sci. 61 (2), 858–873.Google Scholar
Kulkarni, S. D. & Morris, J. F. 2009 Ordering transition and structural evolution under shear in Brownian suspensions. J. Rheol. 53 (2), 417–439.Google Scholar
Ladd, A. J. C. 1994a Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 271, 285–309.Google Scholar
Ladd, A. J. C. 1994b Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 2. Numerical results. J. Fluid Mech. 271, 311–339.Google Scholar
Ladd, A. J. C. & Verberg, R. 2001 Lattice-Boltzmann simulations of particle–fluid suspensions. J. Stat. Phys. 104 (5), 1191–1251.Google Scholar
Lhuillier, D. 2009 Migration of rigid particles in non-Brownian viscous suspensions. Phys. Fluids 21, 023302.CrossRefGoogle Scholar
Lomholt, S. & Maxey, M. R. 2003 Force-coupling method for particulate two-phase flow: Stokes flow. J. Comput. Phys. 184 (2), 381–405.Google Scholar
Maxey, M. R. & Patel, B. K. 2001 Localized force representations for particles sedimenting in Stokes flow. Intl J. Multiphase Flow 27 (9), 1603–1626.Google Scholar
Melrose, J. R. & Ball, R. C. 1995 The pathological behaviour of sheared hard spheres with hydrodynamic interactions. Eur. Phys. Lett. 32, 535–540.Google Scholar
Metzger, B. & Butler, J. E. 2010 Irreversibility and chaos: role of long-range hydrodynamic interactions in sheared suspensions. Phys. Rev. E 82 (5), 051406.Google Scholar
Metzger, B., Pham, P. & Butler, J. E. 2013 Irreversibility and chaos: role of lubrication interactions in sheared suspensions. Phys. Rev. E 87 (5), 052304.Google Scholar
Mills, P. & Snabre, P. 1995 Rheology and structure of concentrated suspensions of hard spheres. Shear induced particle migration. J. Phys. II 5 (10), 1597–1608.Google Scholar
Morris, J. F. 2009 A review of microstructure in concentrated suspensions and its implications for rheology and bulk flow. Rheol. Acta 48 (8), 909–923.Google Scholar
Morris, J. F. & Boulay, F. 1999 Curvilinear flows of noncolloidal suspensions: the role of normal stresses. J. Rheol. 43, 1213–1237.CrossRefGoogle Scholar
Nott, P. R. & Brady, J. F. 1994 Pressure-driven flow of suspensions: simulation and theory. J. Fluid Mech. 275, 157–199.CrossRefGoogle Scholar
Nott, P. R., Guazzelli, E. & Pouliquen, O. 2011 The suspension balance model revisited. Phys. Fluids 23, 043304.Google Scholar
Ovarlez, G., Bertrand, F. & Rodts, S. 2006 Local determination of the constitutive law of a dense suspension of noncolloidal particles through magnetic resonance imaging. J. Rheol. 50, 259–292.Google Scholar
Parsi, F. & Gadala-Maria, F. 1987 Fore-and-aft asymmetry in a concentrated suspension of solid spheres. J. Rheol. 31 (8), 725–732.Google Scholar
Pöschel, T. & Schwager, T. 2005 Computational Granular Dynamics: Models and Algorithms. Springer.Google Scholar
Radjaï, F. & Dubois, F. 2011 Discrete Element Modeling of Granular Materials. John Wiley & Sons, Inc.Google Scholar
Seto, R., Mari, R., Morris, J. & Denn, M. 2013 Discontinuous shear thickening of frictional hard-sphere suspensions. Phys. Rev. Lett. 111 (21), 218301.Google Scholar
Shäfer, J., Dippel, S. & Wolf, D. E. 1996 Force schemes in simulations of granular materials. J. Phys. I 6 (1), 5–20.Google Scholar
Sierou, A. & Brady, J. F. 2002 Rheology and microstructure in concentrated noncolloidal suspensions. J. Rheol. 46, 1031–1056.Google Scholar
Silbert, L. E., Ertaş, D., Grest, G. S., Halsey, T. C., Levine, D. & Plimpton, S. J. 2001 Granular flow down an inclined plane: Bagnold scaling and rheology. Phys. Rev. E 64 (5), 051302.CrossRefGoogle ScholarPubMed
Singh, A. & Nott, P. R. 2000 Normal stresses and microstructure in bounded sheared suspensions via Stokesian dynamics simulations. J. Fluid Mech. 412 (1), 279–301.Google Scholar
Singh, A. & Nott, P. R. 2003 Experimental measurements of the normal stresses in sheared Stokesian suspensions. J. Fluid Mech. 490, 293–320.CrossRefGoogle Scholar
Smart, J. R. & Leighton, D. T. 1989 Measurement of the hydrodynamic surface roughness of noncolloidal spheres. Phys. Fluids A 1 (1), 52–60.Google Scholar
Stickel, J. J. & Powell, R. L. 2005 Fluid mechanics and rheology of dense suspensions. Annu. Rev. Fluid Mech. 37, 129–149.Google Scholar
Wachs, A. 2009 A DEM-DLM/FD method for direct numerical simulation of particulate flows: sedimentation of polygonal isometric particles in a Newtonian fluid with collisions. Comput. Fluids 38 (8), 1608–1628.Google Scholar
Wilson, H. J. 2005 An analytic form for the pair distribution function and rheology of a dilute suspension of rough spheres in plane strain flow. J. Fluid Mech. 534 (1), 97–114.Google Scholar
Wilson, H. & Davis, R. 2000 The viscosity of a dilute suspension of rough spheres. J. Fluid Mech. 421, 339–367.CrossRefGoogle Scholar
Wilson, H. J. & Davis, R. H. 2002 Shear stress of a monolayer of rough spheres. J. Fluid Mech. 452, 425–441.CrossRefGoogle Scholar
Wyart, M. & Cates, M. E. 2014 Discontinuous shear thickening without inertia in dense non-Brownian suspensions. Phys. Rev. Lett. 112 (9), 098302.Google Scholar
Yeo, K. & Maxey, M. R. 2010a Dynamics of concentrated suspensions of non-colloidal particles in Couette flow. J. Fluid Mech. 649 (1), 205–231.Google Scholar
Yeo, K. & Maxey, M. R. 2010b Ordering transition of non-Brownian suspensions in confined steady shear flow. Phys. Rev. E 81 (5), 051502.Google Scholar
Yeo, K. & Maxey, M. R. 2010c Simulation of concentrated suspensions using the force-coupling method. J. Comput. Phys. 229 (6), 2401–2421.Google Scholar
Yu, Z. & Shao, X. 2007 A direct-forcing fictitious domain method for particulate flows. J. Comput. Phys. 227 (1), 292–314.Google Scholar
Zarraga, I. E., Hill, D. A. & Leighton, D. T. Jr 2000 The characterization of the total stress of concentrated suspensions of noncolloidal spheres in Newtonian fluids. J. Rheol. 44, 185–220.CrossRefGoogle Scholar
Zarraga, I. E. & Leighton, D. T. Jr 2001 Normal stress and diffusion in a dilute suspension of hard spheres undergoing simple shear. Phys. Fluids 13, 565–577.Google Scholar