Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ishida, Shunichi
Imai, Yohsuke
Ichikawa, Yuki
Nix, Stephanie
Matsunaga, Daiki
Omori, Toshihiro
and
Ishikawa, Takuji
2016.
A numerical model of a red blood cell infected by Plasmodium falciparum malaria: coupling cell mechanics with ligand-receptor interactions.
Science and Technology of Advanced Materials,
Vol. 17,
Issue. 1,
p.
454.
Matsunaga, D.
Imai, Y.
Wagner, C.
and
Ishikawa, T.
2016.
Reorientation of a single red blood cell during sedimentation.
Journal of Fluid Mechanics,
Vol. 806,
Issue. ,
p.
102.
Aouane, O.
Farutin, A.
Thiébaud, M.
Benyoussef, A.
Wagner, C.
and
Misbah, C.
2017.
Hydrodynamic pairing of soft particles in a confined flow.
Physical Review Fluids,
Vol. 2,
Issue. 6,
Nait Ouhra, A.
Farutin, A.
Aouane, O.
Ez-Zahraouy, H.
Benyoussef, A.
and
Misbah, C.
2018.
Shear thinning and shear thickening of a confined suspension of vesicles.
Physical Review E,
Vol. 97,
Issue. 1,
Rosti, Marco E.
and
Brandt, Luca
2018.
Suspensions of deformable particles in a Couette flow.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 262,
Issue. ,
p.
3.
Saadat, Amir
Guido, Christopher J.
Iaccarino, Gianluca
and
Shaqfeh, Eric S. G.
2018.
Immersed-finite-element method for deformable particle suspensions in viscous and viscoelastic media.
Physical Review E,
Vol. 98,
Issue. 6,
Rosti, Marco E.
Brandt, Luca
and
Mitra, Dhrubaditya
2018.
Rheology of suspensions of viscoelastic spheres: Deformability as an effective volume fraction.
Physical Review Fluids,
Vol. 3,
Issue. 1,
Imai, Yohsuke
and
Matsunaga, Daiki
2018.
Frontiers in Computational Fluid-Structure Interaction and Flow Simulation.
p.
213.
Coclite, Alessandro
and
Gambaruto, Alberto M.
2019.
Injection of Deformable Capsules in a Reservoir: A Systematic Analysis.
Fluids,
Vol. 4,
Issue. 3,
p.
122.
Rosti, Marco E.
De Vita, Francesco
and
Brandt, Luca
2019.
Numerical simulations of emulsions in shear flows.
Acta Mechanica,
Vol. 230,
Issue. 2,
p.
667.
Takeishi, Naoki
Rosti, Marco E.
Imai, Yohsuke
Wada, Shigeo
and
Brandt, Luca
2019.
Haemorheology in dilute, semi-dilute and dense suspensions of red blood cells.
Journal of Fluid Mechanics,
Vol. 872,
Issue. ,
p.
818.
Guido, Christopher J.
and
Shaqfeh, Eric S.G.
2019.
The rheology of soft bodies suspended in the simple shear flow of a viscoelastic fluid.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 273,
Issue. ,
p.
104183.
Ito, Hiroki
Matsunaga, Daiki
and
Imai, Yohsuke
2019.
Shear viscosity of bimodal capsule suspensions in simple shear flow.
Physical Review Fluids,
Vol. 4,
Issue. 11,
De Vita, Francesco
Rosti, Marco Edoardo
Caserta, Sergio
and
Brandt, Luca
2019.
On the effect of coalescence on the rheology of emulsions.
Journal of Fluid Mechanics,
Vol. 880,
Issue. ,
p.
969.
De Vita, Francesco
Rosti, Marco Edoardo
Caserta, Sergio
and
Brandt, Luca
2020.
Numerical simulations of vorticity banding of emulsions in shear flows.
Soft Matter,
Vol. 16,
Issue. 11,
p.
2854.
Sergeev, Yu. S.
Sergeev, S. V.
and
Karpov, G. E.
2020.
Proceedings of the 5th International Conference on Industrial Engineering (ICIE 2019).
p.
1377.
Ishida, Shunichi
and
Matsunaga, Daiki
2020.
Rheology of a dilute ferrofluid droplet suspension in shear flow: Viscosity and normal stress differences.
Physical Review Fluids,
Vol. 5,
Issue. 12,
Filippo Chiara, Luigi
Edoardo Rosti, Marco
Picano, Francesco
and
Brandt, Luca
2020.
Suspensions of deformable particles in Poiseuille flows at finite inertia.
Fluid Dynamics Research,
Vol. 52,
Issue. 6,
p.
065507.
Niu, Ruipeng
and
Pang, Mingjun
2020.
Numerical study on the effect of gravity levels on apparent viscosity of bubbly suspensions.
Microgravity Science and Technology,
Vol. 32,
Issue. 4,
p.
555.
Alizad Banaei, Arash
Rosti, Marco Edoardo
and
Brandt, Luca
2020.
Numerical study of filament suspensions at finite inertia.
Journal of Fluid Mechanics,
Vol. 882,
Issue. ,
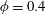 ${\it\phi}=0.4$ by graphics processing unit computing based on the boundary element method with a multipole expansion. To describe the specific viscosity using a polynomial equation of the volume fraction, the coefficients of the equation are calculated by least-squares fitting. The results suggest that the effect of higher-order terms is much smaller for capsule suspensions than rigid sphere suspensions; for example,
${\it\phi}=0.4$ by graphics processing unit computing based on the boundary element method with a multipole expansion. To describe the specific viscosity using a polynomial equation of the volume fraction, the coefficients of the equation are calculated by least-squares fitting. The results suggest that the effect of higher-order terms is much smaller for capsule suspensions than rigid sphere suspensions; for example, 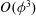 $O({\it\phi}^{3})$ terms account for only 8 % of the specific viscosity even at
$O({\it\phi}^{3})$ terms account for only 8 % of the specific viscosity even at 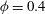 ${\it\phi}=0.4$ for capillary numbers
${\it\phi}=0.4$ for capillary numbers 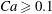 $Ca\geqslant 0.1$. We also investigate the relationship between the deformation and orientation of the capsules and the suspension rheology. When the volume fraction increases, the deformation of the capsules increases while the orientation angle of the capsules with respect to the flow direction decreases. Therefore, both the specific viscosity and the normal stress difference increase with volume fraction due to the increased deformation, whereas the decreased orientation angle suppresses the specific viscosity, but amplifies the normal stress difference.
$Ca\geqslant 0.1$. We also investigate the relationship between the deformation and orientation of the capsules and the suspension rheology. When the volume fraction increases, the deformation of the capsules increases while the orientation angle of the capsules with respect to the flow direction decreases. Therefore, both the specific viscosity and the normal stress difference increase with volume fraction due to the increased deformation, whereas the decreased orientation angle suppresses the specific viscosity, but amplifies the normal stress difference.


