Article contents
Reynolds-number dependence of wall-pressure fluctuations in a pressure-induced turbulent separation bubble
Published online by Cambridge University Press: 07 November 2017
Abstract
Direct numerical simulations are used to examine the behaviour of wall-pressure fluctuations 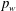 $p_{w}$ in a flat-plate turbulent boundary layer with large adverse and favourable pressure gradients, involving separation and reattachment. The Reynolds number
$p_{w}$ in a flat-plate turbulent boundary layer with large adverse and favourable pressure gradients, involving separation and reattachment. The Reynolds number 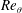 $Re_{\unicode[STIX]{x1D703}}$ based on momentum thickness is equal to 300, 600 and 900. Particular attention is given to effects of Reynolds number on root-mean-square (r.m.s.) values, frequency/power spectra and instantaneous fields. The possible scaling laws are also examined as compared with the existing direct numerical simulation and experimental data. The r.m.s. value of
$Re_{\unicode[STIX]{x1D703}}$ based on momentum thickness is equal to 300, 600 and 900. Particular attention is given to effects of Reynolds number on root-mean-square (r.m.s.) values, frequency/power spectra and instantaneous fields. The possible scaling laws are also examined as compared with the existing direct numerical simulation and experimental data. The r.m.s. value of 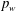 $p_{w}$ normalized by the local maximum Reynolds shear stress
$p_{w}$ normalized by the local maximum Reynolds shear stress 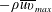 $-\unicode[STIX]{x1D70C}\overline{uv}_{max}$ (Simpson et al. J. Fluid Mech. vol. 177, 1987, pp. 167–186; Na & Moin J. Fluid Mech. vol. 377, 1998b, pp. 347–373) leads to near plateau (i.e.
$-\unicode[STIX]{x1D70C}\overline{uv}_{max}$ (Simpson et al. J. Fluid Mech. vol. 177, 1987, pp. 167–186; Na & Moin J. Fluid Mech. vol. 377, 1998b, pp. 347–373) leads to near plateau (i.e. 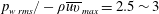 $p_{w\,rms}/-\unicode[STIX]{x1D70C}\overline{uv}_{max}=2.5\sim 3$) in the adverse pressure gradient and separated regions in which the frequency spectra exhibit good collapse at low frequencies. The magnitude of
$p_{w\,rms}/-\unicode[STIX]{x1D70C}\overline{uv}_{max}=2.5\sim 3$) in the adverse pressure gradient and separated regions in which the frequency spectra exhibit good collapse at low frequencies. The magnitude of 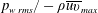 $p_{w\,rms}/-\unicode[STIX]{x1D70C}\overline{uv}_{max}$ is however reduced down to 1.8 near reattachment where good collapse is also obtained with normalization by the local maximum wall-normal Reynolds stress
$p_{w\,rms}/-\unicode[STIX]{x1D70C}\overline{uv}_{max}$ is however reduced down to 1.8 near reattachment where good collapse is also obtained with normalization by the local maximum wall-normal Reynolds stress 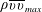 $\unicode[STIX]{x1D70C}\overline{vv}_{max}$. Near reattachment,
$\unicode[STIX]{x1D70C}\overline{vv}_{max}$. Near reattachment, 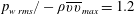 $p_{w\,rms}/-\unicode[STIX]{x1D70C}\overline{vv}_{max}=1.2$ is attained unambiguously independently of the Reynolds number and pressure gradient. The present magnitude (1.2) is smaller than (1.35) obtained for step-induced separation by Ji & Wang (J. Fluid Mech. vol. 712, 2012, pp. 471–504). The reason for this difference is intrinsically associated with convective nature of a pressure-induced separation bubble near reattachment where the magnitude of
$p_{w\,rms}/-\unicode[STIX]{x1D70C}\overline{vv}_{max}=1.2$ is attained unambiguously independently of the Reynolds number and pressure gradient. The present magnitude (1.2) is smaller than (1.35) obtained for step-induced separation by Ji & Wang (J. Fluid Mech. vol. 712, 2012, pp. 471–504). The reason for this difference is intrinsically associated with convective nature of a pressure-induced separation bubble near reattachment where the magnitude of 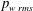 $p_{w\,rms}$ depends essentially on the favourable pressure gradient. The resulting mean flow acceleration leads to delay of the r.m.s. peak after reattachment. Attention is also given to structures of
$p_{w\,rms}$ depends essentially on the favourable pressure gradient. The resulting mean flow acceleration leads to delay of the r.m.s. peak after reattachment. Attention is also given to structures of  $p_{w}$. It is shown that large-scale spanwise rollers of low pressure fluctuations are formed above the bubble, whilst changing to large-scale streamwise elongated structures after reattachment. These large-scale structures become more prominent with increasing
$p_{w}$. It is shown that large-scale spanwise rollers of low pressure fluctuations are formed above the bubble, whilst changing to large-scale streamwise elongated structures after reattachment. These large-scale structures become more prominent with increasing 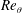 $Re_{\unicode[STIX]{x1D703}}$ and affect
$Re_{\unicode[STIX]{x1D703}}$ and affect 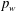 $p_{w}$ significantly.
$p_{w}$ significantly.
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 52
- Cited by



