Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-25T02:24:22.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Revisiting rough-wall turbulent boundary layers over sand-grain roughness

Published online by Cambridge University Press:  28 January 2021

M. Gul Open the ORCID record for M. Gul [Opens in a new window]  and
B. Ganapathisubramani Open the ORCID record for B. Ganapathisubramani [Opens in a new window]
M. Gul*
Affiliation:
Aerodynamics and Flight Mechanics Research Group, University of Southampton, HampshireSO16 7QF, UK
B. Ganapathisubramani
Affiliation:
Aerodynamics and Flight Mechanics Research Group, University of Southampton, HampshireSO16 7QF, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This study examines the flow characteristics of a turbulent boundary layer over different sand-grain roughness created by P$24$ and P$36$ and P$60$ sandpapers. The experimental dataset is acquired with high-resolution planar particle image velocimetry in the streamwise–wall-normal plane for a range of Reynolds number between $\delta ^+=1200\text {--}6300$, which consists of a number of transitionally and fully rough flow conditions where $30\leq \delta /k_s\leq 111$. 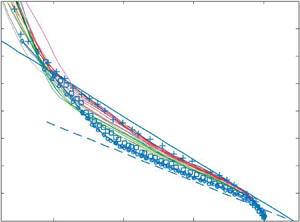The conditions formed over different rough surfaces (having identical surface morphology) enable us to compare rough flows at matched $k_s^+$ or $\delta ^+$ (roughness Reynolds number and Kármán number, respectively), including matched conditions from other studies in the literature. For all the cases, the friction velocity is determined from the direct wall shear-stress measurements using a floating-element drag balance. Mean streamwise velocity profiles exhibit a logarithmic behaviour in the inertial region, and their defect forms are observed to collapse in the outer layer even for the transitionally rough cases at relatively low Reynolds numbers. However, the diagnostic plot of the streamwise velocity intensity suggests that the wall similarity only holds for $k_s^+\geq 75(\Delta U^+\geq 7)$. Analyses at several matched $\delta ^+$ cases show that the mean streamwise velocity defect and turbulence profiles (streamwise and wall-normal velocity variances and the Reynolds shear stress) are self-similar in the outer layer independent of the surface roughness. This similarity extends closer to the wall for the wall-normal velocity variances and Reynolds shear-stress profiles for the weaker roughness (lower $k_s$), which could be a result of higher $\delta /k_s$ for these cases compared with the P$24$ grit sandpaper. For the matched $k_s^+$ conditions, all the profiles were observed to collapse better for fully rough conditions. However, in the transitionally rough regime, the current turbulence statistics are observed to deviate in the outer layer from those reported in other studies (Squire et al., J. Fluid Mech., vol. 795, 2016, pp. 210–240; Morrill-Winter et al., Phys. Rev. Fluids, vol. 2, 2017, 054608). Higher values of roughness function, turbulence intensity and Reynolds shear stress in the current study could be due to overstimulation of the boundary layer. Despite the differences in the turbulence profiles observed, the average large-scale structures across all wall-normal locations are found to be independent of $k_s^+$ and $\delta ^+$.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 911 , 25 March 2021 , A26
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alfredsson, P.H., Orlu, R. & Segalini, A. 2012 A new formulation for the streamwise turbulence intensity distribution in wall-bounded turbulent flows. Eur. J. Mech. B/Fluids 36, 167–175.CrossRefGoogle Scholar
Alfredsson, P.H., Segalini, A. & Orlu, R. 2011 A new scaling for the streamwise turbulence intensity in wall-bounded turbulent flows and what it tells us about the “outer” peak. Phys. Fluids 23, 041702.CrossRefGoogle Scholar
Bhaganagar, K., Kim, J. & Coleman, G. 2004 Effect of roughness on wall-bounded turbulence. Flow Turbul. Combust. 72 (2–4), 463–492.CrossRefGoogle Scholar
Brzek, B.G., Cal, R.B. & Johansson, G. 2008 Transitionally rough zero pressure gradient turbulent boundary layers. Exp. Fluids 44, 115–124.CrossRefGoogle Scholar
Carlier, J. & Stanislas, M. 2005 Experimental study of eddy structures in a turbulent boundary layer using particle image velocimetry. J. Fluid Mech. 535, 143–188.CrossRefGoogle Scholar
Castro, I.P. 2007 Rough-wall boundary layers: mean flow universality. J. Fluid Mech. 585, 469–485.CrossRefGoogle Scholar
Castro, I.P., Segalini, A. & Alfredsson, P.H. 2013 Outer-layer turbulence intensities in smooth- and rough-wall boundary layers. J. Fluid Mech. 727, 119–131.CrossRefGoogle Scholar
Chan, L., MacDonald, M., Chung, D., Hutchins, N. & Ooi, A. 2015 A systematic investigation of roughness height and wavelength in turbulent pipe flow in the transitionally rough regime. J. Fluid Mech. 771, 743–777.CrossRefGoogle Scholar
Chauhan, K.A., Monkewitz, P.A. & Nagib, H. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41, 021404.CrossRefGoogle Scholar
Coles, D. 1956 The law of the wake in the turbulent boundary layer. J. Fluid Mech. 1, 191–226.CrossRefGoogle Scholar
Ferreira, M.A., Rodriguez-Lopez, E. & Ganapathisubramani, B. 2018 An alternative floating element design for skin-friction measurement of turbulent wall flows. Exp. Fluids 59 (10), 155.CrossRefGoogle Scholar
Flack, K.A., Schultz, M.P. & Connelly, J.S. 2007 Examination of a critical roughness height for outer layer similarity. Phys. Fluids 19, 095104.CrossRefGoogle Scholar
Flores, O. & Jimenez, J. 2006 Effect of wall-boundary disturbances on turbulent channel flows. J. Fluid Mech. 566, 357–376.CrossRefGoogle Scholar
Hong, J., Katz, J. & Schultz, M.P. 2011 Near-wall turbulence statistics and flow structures over three-dimensional roughness in a turbulent channel flow. J. Fluid Mech. 667, 1–37.CrossRefGoogle Scholar
Hultmark, M., Vallikivi, M., Bailey, S.C. & Smits, A. 2013 Logarithmic scaling of turbulence in smooth- and rough-wall pipe flow. J. Fluid Mech. 728, 376–395.CrossRefGoogle Scholar
Hutchins, N., Monty, J.P., Ganapathisubramani, B., Ng, H.C.H. & Marusic, I. 2011 Three-dimensional conditional structure of a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 673, 255–285.CrossRefGoogle Scholar
Jimenez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.CrossRefGoogle Scholar
Keirsbulck, L., Labraga, L., Mazouz, A. & Tournier, C. 2002 Surface roughness effects on turbulent boundary layer structures. Trans. ASME: J. Fluids Engng 124 (1), 127–135.Google Scholar
Krogstad, P.A., Antonia, R.A. & Browne, L.W.B. 1992 Comparison between rough- and smooth-wall turbulent boundary layers. J. Fluid Mech. 245, 599–617.CrossRefGoogle Scholar
Lee, S.H. & Sung, H.J. 2007 Direct numerical simulation of the turbulent boundary layer over a rod-roughened wall. J. Fluid Mech. 584, 125–146.CrossRefGoogle Scholar
Lu, S.S. & Willmarth, W.W. 1973 Measurements of the structure of the Reynolds stress in a turbulent boundary layer. J. Fluid Mech. 60, 481.CrossRefGoogle Scholar
Moody, L.F. 1944 Friction factors for pipe flow. Trans. ASME 66, 671.Google Scholar
Morrill-Winter, C., Squire, D.T., Klewicki, J.C., Hutchins, N., Schultz, M.P. & Marusic, I. 2017 Reynolds number and roughness effects on turbulent stresses in sandpaper roughness boundary layers. Phys. Rev. Fluids 2, 054608.CrossRefGoogle Scholar
Nikuradse, J. 1933 Laws of flow in rough pipes. VDI Forschungsheft 361. In translation, NACA TM 1292, 1950.Google Scholar
Placidi, M. & Ganapathisubramani, B. 2018 Turbulent flow over large roughness elements: effect of frontal and plan solidity on turbulence statistics and structure. Boundary-Layer Meteorol. 167, 99–121.CrossRefGoogle ScholarPubMed
Raupach, M.R. 1981 Conditional statistics of Reynolds stress in rough-wall and smooth-wall turbulent boundary layers. J. Fluid Mech. 108, 363–382.CrossRefGoogle Scholar
Schlichting, H. 1936 Experimentelle untersuchungen zum rauhigkeitsproblem. Ing.-Arch. 7, 1–34.CrossRefGoogle Scholar
Schlichting, H. 1979 Boundary-Layer Theory, 7th edn. McGraw-Hill.Google Scholar
Schultz, M.P. & Flack, K.A. 2007 The rough-wall turbulent boundary layer from the hydraulically smooth to the fully rough regime. J. Fluid Mech. 580, 381–405.CrossRefGoogle Scholar
Schultz, M. & Flack, K.A. 2009 Turbulent boundary layers on a systematically varied rough wall. Phys. Fluids 21, 015104.CrossRefGoogle Scholar
Shockling, M.A., Alle, J.J. & Smits, A.J. 2006 Roughness effects in turbulent pipe flow. J. Fluid Mech. 564, 267–285.CrossRefGoogle Scholar
Sillero, J.A., Jimeenez, J. & Moser, R.D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to $\delta ^+ \approx 2000$. Phys. Fluids 25, 105102.CrossRefGoogle Scholar
Squire, D.T., Morrill-Winter, C., Hutchins, N., Schultz, M.P., Klewicki, J.C. & Marusic, I. 2016 Comparison of turbulent boundary layers over smooth and rough surfaces up to high Reynolds numbers. J. Fluid Mech. 795, 210–240.CrossRefGoogle Scholar
Townsend, A.A. 1956 The structure of turbulent shear flow, vol. 1. Cambridge University Press.Google Scholar
Volino, R.J., Schultz, M.P. & Flack, K.A. 2009 Turbulence structure in a boundary layer with two-dimensional roughness. J. Fluid Mech. 635, 75–101.CrossRefGoogle Scholar