Article contents
Revisiting ignited–quenched transition and the non-Newtonian rheology of a sheared dilute gas–solid suspension
Published online by Cambridge University Press: 03 November 2017
Abstract
The hydrodynamics and rheology of a sheared dilute gas–solid suspension, consisting of inelastic hard spheres suspended in a gas, are analysed using an anisotropic Maxwellian as the single particle distribution function. For the simple shear flow, the closed-form solutions for granular temperature and three invariants of the second-moment tensor are obtained as functions of the Stokes number (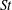 $St$), the mean density (
$St$), the mean density ( $\unicode[STIX]{x1D708}$) and the restitution coefficient (
$\unicode[STIX]{x1D708}$) and the restitution coefficient ( $e$). Multiple states of high and low temperatures are found when the Stokes number is small, thus recovering the ‘ignited’ and ‘quenched’ states, respectively, of Tsao & Koch (J. Fluid Mech., vol. 296, 1995, pp. 211–246). The phase diagram is constructed in the three-dimensional (
$e$). Multiple states of high and low temperatures are found when the Stokes number is small, thus recovering the ‘ignited’ and ‘quenched’ states, respectively, of Tsao & Koch (J. Fluid Mech., vol. 296, 1995, pp. 211–246). The phase diagram is constructed in the three-dimensional (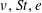 $\unicode[STIX]{x1D708},St,e$)-space that delineates the regions of ignited and quenched states and their coexistence. The particle-phase shear viscosity and the normal-stress differences are analysed, along with related scaling relations on the quenched and ignited states. At any
$\unicode[STIX]{x1D708},St,e$)-space that delineates the regions of ignited and quenched states and their coexistence. The particle-phase shear viscosity and the normal-stress differences are analysed, along with related scaling relations on the quenched and ignited states. At any  $e$, the shear viscosity undergoes a discontinuous jump with increasing shear rate at the ‘quenched–ignited’ transition. The first (
$e$, the shear viscosity undergoes a discontinuous jump with increasing shear rate at the ‘quenched–ignited’ transition. The first (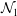 ${\mathcal{N}}_{1}$) and second (
${\mathcal{N}}_{1}$) and second (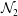 ${\mathcal{N}}_{2}$) normal-stress differences also undergo similar first-order transitions: (i)
${\mathcal{N}}_{2}$) normal-stress differences also undergo similar first-order transitions: (i) 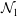 ${\mathcal{N}}_{1}$ jumps from large to small positive values and (ii)
${\mathcal{N}}_{1}$ jumps from large to small positive values and (ii)  ${\mathcal{N}}_{2}$ from positive to negative values with increasing
${\mathcal{N}}_{2}$ from positive to negative values with increasing 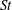 $St$, with the sign change of
$St$, with the sign change of 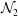 ${\mathcal{N}}_{2}$ identified with the system making a transition from the quenched to ignited states. The superior prediction of the present theory over the standard Grad’s method and the Burnett-order Chapman–Enskog solution is demonstrated via comparisons of transport coefficients with simulation data for a range of Stokes number and restitution coefficient.
${\mathcal{N}}_{2}$ identified with the system making a transition from the quenched to ignited states. The superior prediction of the present theory over the standard Grad’s method and the Burnett-order Chapman–Enskog solution is demonstrated via comparisons of transport coefficients with simulation data for a range of Stokes number and restitution coefficient.
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 27
- Cited by


