Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-12-01T01:46:04.441Z Has data issue: false hasContentIssue false
  • English
  • Français

Reversals of the large-scale circulation in quasi-2D Rayleigh–Bénard convection

Published online by Cambridge University Press:  04 August 2015

Rui Ni ,
Shi-Di Huang  and
Ke-Qing Xia
Rui Ni
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
Shi-Di Huang
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
Ke-Qing Xia*
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

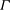We report an experimental study of the large-scale circulation (LSC) reversal in quasi-2D turbulent thermal convection, in which the aspect ratio ${\it\Gamma}$ (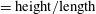$=\text{height}/\text{length}$ of a rectangular box) is used as a parameter to perturb the stability of the LSC. It is found that the mean time interval 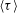$\langle {\it\tau}\rangle$ between two successive reversals increases strongly with increasing 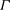${\it\Gamma}$. A stochastic model is proposed to incorporate the effect of the corner rolls. In the model, the aspect ratio serves as a tuning parameter for the relative weight of the corner rolls that damp the LSC. The model predictions for the shape of the bistable states of the system and 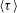$\langle {\it\tau}\rangle$ agree excellently with the experimental results, with 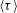$\langle {\it\tau}\rangle$ having an unexpected stretched exponential Rayleigh number dependence, 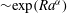${\sim}\!\exp (Ra^{{\it\alpha}})$. We further show quantitatively that the main damping force of the LSC in a quasi-2D system is from the corner rolls rather than the viscous drag from the sidewalls, which bridges the difference found in quasi-2D and 3D systems.

JFM classification

Convection: Plumes/thermals Turbulent Flows: Turbulent convection
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 778 , 10 September 2015 , R5
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Department of Mechanical and Nuclear Engineering, Pennsylvania State University, State College, PA 16802-1412, USA.

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Araujo, F. F., Grossmann, S. & Lohse, D. 2005 Wind reversals in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95 (8), 084502.Google Scholar
Assaf, M., Angheluta, L. & Goldenfeld, N. 2011 Rare fluctuations and large-scale circulation cessations in turbulent convection. Phys. Rev. Lett. 107, 044502.Google Scholar
Benzi, R. 2005 Flow reversal in a simple dynamical model of turbulence. Phys. Rev. Lett. 95 (2), 024502.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2006 Rotations and cessations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 568, 351–386.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2007 Large-scale circulation model for turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 98 (13), 134501.CrossRefGoogle ScholarPubMed
Brown, E. & Ahlers, G. 2008 A model of diffusion in a potential well for the dynamics of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Fluids 20 (7), 075101.Google Scholar
Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Reorientation of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95, 084503.CrossRefGoogle ScholarPubMed
Chandra, M. & Verma, M. K. 2011 Dynamics and symmetries of flow reversals in turbulent convection. Phys. Rev. E 83 (6), 067303.CrossRefGoogle ScholarPubMed
Chandra, M. & Verma, M. K. 2013 Flow reversals in turbulent convection via vortex reconnections. Phys. Rev. Lett. 110 (11), 114503.Google Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. 35, 58.Google Scholar
Cioni, S., Ciliberto, S. & Sommeria, J. 1997 Strongly turbulent Rayleigh–Bénard convection in mercury: comparison with results at moderate Prandtl number. J. Fluid Mech. 335, 111–140.Google Scholar
van Doorn, E., Dhruva, B., Sreenivasan, K. & Cassella, V. 2000 Statistics of wind direction and its increments. Phys. Fluids 12, 1529–1534.CrossRefGoogle Scholar
Gardiner, C. W. 2004 Handbook of Stochastic Methods. Springer.CrossRefGoogle Scholar
Glatzmaier, G. A., Coe, R. S., Hongre, L. & Roberts, P. H. 1999 The role of the Earth’s mantle in controlling the frequency of geomagnetic reversals. Nature 401, 885–890.Google Scholar
He, X.-Z., Tong, P. & Xia, K.-Q. 2007 Measured thermal dissipation field in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 98, 144501.Google Scholar
Kadanoff, L. 2001 Turbulent heat flow: structures and scaling. Phys. Today 54 (8), 34.Google Scholar
Lam, S., Shang, X.-D., Zhou, S.-Q. & Xia, K.-Q. 2002 Prandtl number dependence of the viscous boundary layer and the Reynolds numbers in Rayleigh–Bénard convection. Phys. Rev. E 65, 066306.Google Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.Google Scholar
Sreenivasan, K. R., Bershadskii, A. & Niemela, J. J. 2002 Mean wind and its reversal in thermal convection. Phys. Rev. E 65, 056306.CrossRefGoogle ScholarPubMed
Sugiyama, K., Ni, R., Stevens, R. J. A. M., Chan, T.-S., Zhou, S.-Q., Xi, H.-D., Sun, C., Grossmann, S., Xia, K.-Q. & Lohse, D. 2010 Flow reversals in thermally driven turbulence. Phys. Rev. Lett. 105, 034503.Google Scholar
Sun, C., Xi, H.-D. & Xia, K.-Q. 2005 Azimuthal symmetry, flow dynamics, and heat transport in turbulent thermal convection in a cylinder with an aspect ratio of 0.5. Phys. Rev. Lett. 95, 074502.Google Scholar
Tsuji, Y., Mizuno, T., Mashiko, T. & Sano, M. 2005 Mean wind in convective turbulence of mercury. Phys. Rev. Lett. 94 (3), 034501.Google Scholar
Vasilev, A., Yu & Frick, P. G. 2011 Reversals of large-scale circulation in turbulent convection in rectangular cavities. JETP Lett. 93, 330–334.Google Scholar
Wagner, S. & Shishkina, O. 2013 Aspect-ratio dependency of Rayleigh–Bénard convection in box-shaped containers. Phys. Fluids 25 (8), 085110.CrossRefGoogle Scholar
Xi, H.-D., Lam, S. & Xia, K.-Q. 2004 From laminar plumes to organized flows: the onset of large-scale circulation in turbulent thermal convection. J. Fluid Mech. 503, 47–56.Google Scholar
Xi, H.-D. & Xia, K.-Q. 2007 Cessations and reversals of the large-scale circulation in turbulent thermal convection. Phys. Rev. E 75 (6), 066307.Google Scholar
Xi, H.-D., Zhou, Q. & Xia, K.-Q. 2006 Azimuthal motion of the mean wind in turbulent thermal convection. Phys. Rev. E 73 (5), 056312.CrossRefGoogle ScholarPubMed
Xia, K.-Q. 2013 Current trends and future directions in turbulent thermal convection. Theor. Appl. Mech. Lett. 3, 052001.Google Scholar
Xia, K.-Q., Sun, C. & Zhou, S.-Q. 2003 Particle image velocimetry measurement of the velocity field in turbulent thermal convection. Phys. Rev. E 68, 066303.CrossRefGoogle ScholarPubMed
Xia, K.-Q., Zhou, S.-Q. & Sun, C. 2005 Statistics and scaling of the velocity field in turbulent thermal convection. In Progress in Turbulence, pp. 163–170.Google Scholar
Yanagisawa, T., Yamagishi, Y., Hamano, Y., Tasaka, Y. & Takeda, Y. 2011 Spontaneous flow reversals in Rayleigh–Bénard convection of a liquid metal. Phys. Rev. E 83 (3), 036307.Google Scholar
Zhou, Q. & Xia, K.-Q. 2010 Physical and geometrical properties of thermal plumes in turbulent Rayleigh–Bénard convection. New J. Phys. 12, 075006.Google Scholar