1. Introduction
The spatial and temporal fluctuations at small scales in fluid turbulence, which are highly non-Gaussian and long-range correlated (Mordant, Lévêque & Pinton Reference Mordant, Lévêque and Pinton2004b), are among the most complex and consequential phenomena in fluid mechanics. The velocity gradient, as well as the velocity increment between two points, is found to be highly intermittent with extreme events occurring more frequently as the Reynolds number increases (Yeung, Zhai & Sreenivasan Reference Yeung, Zhai and Sreenivasan2015). One possible mechanism for the enhanced intermittency at small scales is related to the nonlinear self-amplification of the velocity gradient tensor ![]() ${\mathsf{A}}_{ij} = \partial u_{i}/\partial x_{j}$ during its Lagrangian evolution, where
${\mathsf{A}}_{ij} = \partial u_{i}/\partial x_{j}$ during its Lagrangian evolution, where ![]() $u_{i}$ is the fluid velocity component in direction
$u_{i}$ is the fluid velocity component in direction ![]() $x_{i}$. This process is directly linked to the classic energy cascade picture in turbulence in which large eddies are assumed to fragment into small eddies (Kolmogorov Reference Kolmogorov1941) with energy transferring from large to small scales.
$x_{i}$. This process is directly linked to the classic energy cascade picture in turbulence in which large eddies are assumed to fragment into small eddies (Kolmogorov Reference Kolmogorov1941) with energy transferring from large to small scales.
In addition to the intrinsic strong intermittency, further universal behaviours of ![]() ${\mathsf{A}}_{ij}$ include the negative skewness of the longitudinal velocity gradient (Sreenivasan & Antonia Reference Sreenivasan and Antonia1997), and the preferential alignment between vorticity and the eigenvector associated with the intermediate eigenvalue of the rate-of-strain tensor (Kerr Reference Kerr1985; Elsinga & Marusic Reference Elsinga and Marusic2010b; Xu, Pumir & Bodenschatz Reference Xu, Pumir and Bodenschatz2011). Moreover, the joint probability density function (p.d.f.) of the invariants
${\mathsf{A}}_{ij}$ include the negative skewness of the longitudinal velocity gradient (Sreenivasan & Antonia Reference Sreenivasan and Antonia1997), and the preferential alignment between vorticity and the eigenvector associated with the intermediate eigenvalue of the rate-of-strain tensor (Kerr Reference Kerr1985; Elsinga & Marusic Reference Elsinga and Marusic2010b; Xu, Pumir & Bodenschatz Reference Xu, Pumir and Bodenschatz2011). Moreover, the joint probability density function (p.d.f.) of the invariants ![]() $Q = - {\mathsf{A}}_{ij}{\mathsf{A}}_{ji}/2$ and
$Q = - {\mathsf{A}}_{ij}{\mathsf{A}}_{ji}/2$ and ![]() $R = - {\mathsf{A}}_{ij}{\mathsf{A}}_{jk}{\mathsf{A}}_{ki}/3$ is found to exhibit a universal teardrop shape (figure 1b), with higher probability along the Vieillefosse tail
$R = - {\mathsf{A}}_{ij}{\mathsf{A}}_{jk}{\mathsf{A}}_{ki}/3$ is found to exhibit a universal teardrop shape (figure 1b), with higher probability along the Vieillefosse tail ![]() $27R^{2}/4 + Q^{3} = 0$ (Vieillefosse Reference Vieillefosse1982, Reference Vieillefosse1984; Meneveau Reference Meneveau2011) for various Reynolds number and flow configurations (Soria et al. Reference Soria, Sondergaard, Cantwell, Chong and Perry1994; Chong et al. Reference Chong, Soria, Perry, Chacin, Cantwell and Na1998; Lüthi, Holzner & Tsinober Reference Lüthi, Holzner and Tsinober2009; Elsinga & Marusic Reference Elsinga and Marusic2010a; Lozano-Durán, Holzner & Jiménez Reference Lozano-Durán, Holzner and Jiménez2016). These behaviours reflect fundamental processes involved in turbulent flows, e.g. vortex stretching and strain self-amplification.
$27R^{2}/4 + Q^{3} = 0$ (Vieillefosse Reference Vieillefosse1982, Reference Vieillefosse1984; Meneveau Reference Meneveau2011) for various Reynolds number and flow configurations (Soria et al. Reference Soria, Sondergaard, Cantwell, Chong and Perry1994; Chong et al. Reference Chong, Soria, Perry, Chacin, Cantwell and Na1998; Lüthi, Holzner & Tsinober Reference Lüthi, Holzner and Tsinober2009; Elsinga & Marusic Reference Elsinga and Marusic2010a; Lozano-Durán, Holzner & Jiménez Reference Lozano-Durán, Holzner and Jiménez2016). These behaviours reflect fundamental processes involved in turbulent flows, e.g. vortex stretching and strain self-amplification.

Figure 1. (a) The ![]() $Q$–
$Q$–![]() $R$ trajectories of the restricted Euler model in 3-D turbulence. (b) The joint p.d.f. of
$R$ trajectories of the restricted Euler model in 3-D turbulence. (b) The joint p.d.f. of ![]() $Q$ and
$Q$ and ![]() $R$ of 3-D homogeneous and isotropic turbulence. Here,
$R$ of 3-D homogeneous and isotropic turbulence. Here, ![]() ${\mathsf{S}}_{ij}$ is the rate-of-strain tensor. Panels (a,b) are adapted with permission from Johnson & Wilczek (Reference Johnson and Wilczek2024). (c) The joint p.d.f. of
${\mathsf{S}}_{ij}$ is the rate-of-strain tensor. Panels (a,b) are adapted with permission from Johnson & Wilczek (Reference Johnson and Wilczek2024). (c) The joint p.d.f. of ![]() $p$ and
$p$ and ![]() $q$ along a 2-D section of 3-D turbulence. Panel (c) is adapted with permission from Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013).
$q$ along a 2-D section of 3-D turbulence. Panel (c) is adapted with permission from Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013).
Dynamic system models from a Lagrangian point of view provide a powerful tool to study the evolution of the velocity gradient and connect dynamics, statistics and structures of turbulence in a unified framework (Meneveau Reference Meneveau2011; Johnson & Wilczek Reference Johnson and Wilczek2024). By taking the spatial gradient of the Navier–Stokes equation and neglecting the terms involving the viscous effect and anisotropic pressure Hessian, Vieillefosse (Reference Vieillefosse1982, Reference Vieillefosse1984) and Cantwell (Reference Cantwell1992) derived the restricted Euler model,
where ![]() $\delta _{ij}$ is the Kronecker delta function. Despite the simplifying assumptions, the restricted Euler model captures the self-amplification of the velocity gradient and is remarkably successful at predicting its aforementioned key features, including the teardrop shape observed in the joint p.d.f. of invariants. This model has further inspired subsequent works (Girimaji & Pope Reference Girimaji and Pope1990; Chevillard & Meneveau Reference Chevillard and Meneveau2006; Biferale et al. Reference Biferale, Chevillard, Meneveau and Toschi2007; Chevillard et al. Reference Chevillard, Meneveau, Biferale and Toschi2008; Wilczek & Meneveau Reference Wilczek and Meneveau2014; Johnson & Meneveau Reference Johnson and Meneveau2016) which have attempted to obtain more accurate turbulent statistics by modelling the unclosed terms.
$\delta _{ij}$ is the Kronecker delta function. Despite the simplifying assumptions, the restricted Euler model captures the self-amplification of the velocity gradient and is remarkably successful at predicting its aforementioned key features, including the teardrop shape observed in the joint p.d.f. of invariants. This model has further inspired subsequent works (Girimaji & Pope Reference Girimaji and Pope1990; Chevillard & Meneveau Reference Chevillard and Meneveau2006; Biferale et al. Reference Biferale, Chevillard, Meneveau and Toschi2007; Chevillard et al. Reference Chevillard, Meneveau, Biferale and Toschi2008; Wilczek & Meneveau Reference Wilczek and Meneveau2014; Johnson & Meneveau Reference Johnson and Meneveau2016) which have attempted to obtain more accurate turbulent statistics by modelling the unclosed terms.
More recently, Cardesa et al. (Reference Cardesa, Mistry, Gan and Dawson2013) measured the ![]() $2\times 2$ reduced velocity gradient tensor
$2\times 2$ reduced velocity gradient tensor ![]() ${\tilde {{\mathsf{A}}}}_{ij}$ along a two-dimensional (2-D) section of three-dimensional (3-D) turbulence. The joint p.d.f. of velocity gradient invariants (
${\tilde {{\mathsf{A}}}}_{ij}$ along a two-dimensional (2-D) section of three-dimensional (3-D) turbulence. The joint p.d.f. of velocity gradient invariants (![]() $\,p$ and
$\,p$ and ![]() $q$) exhibits a universal teapot pattern for various flow configurations, as illustrated in figure 1(c). Although the underlying mechanism leading to the teapot pattern is still not completely understood, the asymmetry of the pattern is found to be associated with the predominance of vortex stretching over compression in 3-D turbulence.
$q$) exhibits a universal teapot pattern for various flow configurations, as illustrated in figure 1(c). Although the underlying mechanism leading to the teapot pattern is still not completely understood, the asymmetry of the pattern is found to be associated with the predominance of vortex stretching over compression in 3-D turbulence.
Despite the progress in the understanding and predicting the dynamics of ![]() ${\mathsf{A}}_{ij}$ in 3-D turbulence, insights of the reduced velocity gradient tensor
${\mathsf{A}}_{ij}$ in 3-D turbulence, insights of the reduced velocity gradient tensor ![]() ${\tilde {{\mathsf{A}}}}_{ij}$ in free-surface turbulence, to our best knowledge, are still lacking. Here, we define
${\tilde {{\mathsf{A}}}}_{ij}$ in free-surface turbulence, to our best knowledge, are still lacking. Here, we define ![]() ${\tilde {{\mathsf{A}}}}_{ij}$ being the top left-hand
${\tilde {{\mathsf{A}}}}_{ij}$ being the top left-hand ![]() $2 \times 2$ block of the full velocity gradient
$2 \times 2$ block of the full velocity gradient ![]() ${\mathsf{A}}_{ij}$, with
${\mathsf{A}}_{ij}$, with ![]() $i,j = 1,2$ representing the surface-parallel directions. Here
$i,j = 1,2$ representing the surface-parallel directions. Here ![]() ${\tilde {{\mathsf{A}}}}_{ij}$ is related to multiple fundamental features of free-surface turbulence, such as surface deformation (Babiker et al. Reference Babiker, Bjerkebæk, Xuan, Shen and Ellingsen2023), compressible velocity field (Boffetta, De Lillo & Gamba Reference Boffetta, De Lillo and Gamba2004), exchange of mass between the free surface and the bulk (McKenna & McGillis Reference McKenna and McGillis2004; Herlina & Wissink Reference Herlina and Wissink2019) and its intermittent nature (Goldburg et al. Reference Goldburg, Cressman, Vörös, Eckhardt and Schumacher2001; Li et al. Reference Li, Wang, Qi and Coletti2024). These features affect a variety of large-scale phenomena including the exchange of gas between the atmosphere and ocean (Jähne & Haußecker Reference Jähne and Haußecker1998; Veron Reference Veron2015), the transport of oceanic pollutants such as microplastics (Zhang Reference Zhang2017; Mountford & Morales Maqueda Reference Mountford and Morales Maqueda2019; van Emmerik & Schwarz Reference van Emmerik and Schwarz2020) and the blooming of phytoplankton (Durham et al. Reference Durham, Climent, Barry, De Lillo, Boffetta, Cencini and Stocker2013; Lindemann, Visser & Mariani Reference Lindemann, Visser and Mariani2017). In this work, we developed a restricted Euler model for the reduced velocity gradient tensor
${\tilde {{\mathsf{A}}}}_{ij}$ is related to multiple fundamental features of free-surface turbulence, such as surface deformation (Babiker et al. Reference Babiker, Bjerkebæk, Xuan, Shen and Ellingsen2023), compressible velocity field (Boffetta, De Lillo & Gamba Reference Boffetta, De Lillo and Gamba2004), exchange of mass between the free surface and the bulk (McKenna & McGillis Reference McKenna and McGillis2004; Herlina & Wissink Reference Herlina and Wissink2019) and its intermittent nature (Goldburg et al. Reference Goldburg, Cressman, Vörös, Eckhardt and Schumacher2001; Li et al. Reference Li, Wang, Qi and Coletti2024). These features affect a variety of large-scale phenomena including the exchange of gas between the atmosphere and ocean (Jähne & Haußecker Reference Jähne and Haußecker1998; Veron Reference Veron2015), the transport of oceanic pollutants such as microplastics (Zhang Reference Zhang2017; Mountford & Morales Maqueda Reference Mountford and Morales Maqueda2019; van Emmerik & Schwarz Reference van Emmerik and Schwarz2020) and the blooming of phytoplankton (Durham et al. Reference Durham, Climent, Barry, De Lillo, Boffetta, Cencini and Stocker2013; Lindemann, Visser & Mariani Reference Lindemann, Visser and Mariani2017). In this work, we developed a restricted Euler model for the reduced velocity gradient tensor ![]() ${\tilde {{\mathsf{A}}}}_{ij}$ at an undeformed free surface, from which the dynamic equations of the invariants are obtained. This model provides new insights on various fundamental features of free-surface turbulence, including its enhanced intermittency observed in laboratory experiments. Deviations from the observations suggest directions to further improve the modelling framework. This paper is organized as follows. In § 2, we introduce the restricted Euler model for free-surface flows. This model is then compared with experimental data in § 3. Section 4 summarizes our findings and draws conclusions.
${\tilde {{\mathsf{A}}}}_{ij}$ at an undeformed free surface, from which the dynamic equations of the invariants are obtained. This model provides new insights on various fundamental features of free-surface turbulence, including its enhanced intermittency observed in laboratory experiments. Deviations from the observations suggest directions to further improve the modelling framework. This paper is organized as follows. In § 2, we introduce the restricted Euler model for free-surface flows. This model is then compared with experimental data in § 3. Section 4 summarizes our findings and draws conclusions.
2. Restricted Euler model
We begin with adapting the restricted Euler model originally derived for 3-D turbulence (see (1.1)). For homogeneous and isotropic free-surface turbulence, the shear-free boundary condition on the free surface requires the derivative of horizontal velocity along the vertical direction to be zero, i.e. ![]() $\partial u_1/\partial x_3=\partial u_2/\partial x_3=0$. We further focus on the situation in which the surface deformation is negligible, which is the case in a wide range of naturally occurring water flows (Brocchini & Peregrine Reference Brocchini and Peregrine2001). Then, the no-penetration condition requires the vertical velocity on the free surface to also be zero, i.e.
$\partial u_1/\partial x_3=\partial u_2/\partial x_3=0$. We further focus on the situation in which the surface deformation is negligible, which is the case in a wide range of naturally occurring water flows (Brocchini & Peregrine Reference Brocchini and Peregrine2001). Then, the no-penetration condition requires the vertical velocity on the free surface to also be zero, i.e. ![]() $u_3=0$. This further leads to
$u_3=0$. This further leads to ![]() $\partial u_3/\partial x_1=\partial u_3/\partial x_2=0$. Combining both boundary conditions, we write
$\partial u_3/\partial x_1=\partial u_3/\partial x_2=0$. Combining both boundary conditions, we write
By setting ![]() $i,j = 1,2$ while keeping
$i,j = 1,2$ while keeping ![]() $k,m = 1,2,3$ in (1.1), the restricted Euler model reduces to the transport equation for
$k,m = 1,2,3$ in (1.1), the restricted Euler model reduces to the transport equation for ![]() ${\tilde {{\mathsf{A}}}}_{ij}$ which still contains terms such as
${\tilde {{\mathsf{A}}}}_{ij}$ which still contains terms such as ![]() ${\mathsf{A}}_{13}$ and
${\mathsf{A}}_{13}$ and ![]() ${\mathsf{A}}_{33}$. By further applying the shear-free and no-penetration boundary conditions on the free surface (see (2.1)) and the incompressibility condition
${\mathsf{A}}_{33}$. By further applying the shear-free and no-penetration boundary conditions on the free surface (see (2.1)) and the incompressibility condition ![]() ${\mathsf{A}}_{33} = - {\mathsf{A}}_{11} - {\mathsf{A}}_{22} = - \mathrm {tr}( {\tilde {{\mathsf{A}}}}_{ij} )$, these terms are eliminated and (1.1) becomes the restricted Euler equation on the free surface:
${\mathsf{A}}_{33} = - {\mathsf{A}}_{11} - {\mathsf{A}}_{22} = - \mathrm {tr}( {\tilde {{\mathsf{A}}}}_{ij} )$, these terms are eliminated and (1.1) becomes the restricted Euler equation on the free surface:
Equation (2.2) provides a simplified model for the Lagrangian evolution of the reduced velocity gradient tensor in non-wavy free-surface turbulence. Here, ![]() ${\tilde {{\mathsf{A}}}}_{ik}{\tilde {{\mathsf{A}}}}_{kj}$ is the nonlinear self-amplification term that accounts for the enhanced intermittency, while the term
${\tilde {{\mathsf{A}}}}_{ik}{\tilde {{\mathsf{A}}}}_{kj}$ is the nonlinear self-amplification term that accounts for the enhanced intermittency, while the term ![]() ${\tilde {{\mathsf{A}}}}_{nn}^{2}$ signals the role of the non-solenoidal nature of the surface flow.
${\tilde {{\mathsf{A}}}}_{nn}^{2}$ signals the role of the non-solenoidal nature of the surface flow.
Given the restricted Euler model for ![]() ${\tilde {{\mathsf{A}}}}_{ij}$, the Lagrangian evolution equations for the invariants
${\tilde {{\mathsf{A}}}}_{ij}$, the Lagrangian evolution equations for the invariants ![]() $p = - \mathrm {tr}( {\tilde {{\mathsf{A}}}}_{ij} ) = - {\tilde {{\mathsf{A}}}}_{11} - {\tilde {{\mathsf{A}}}}_{22}$ and
$p = - \mathrm {tr}( {\tilde {{\mathsf{A}}}}_{ij} ) = - {\tilde {{\mathsf{A}}}}_{11} - {\tilde {{\mathsf{A}}}}_{22}$ and ![]() $q = \mathrm {det}( {\tilde {{\mathsf{A}}}}_{ij} ) = {\tilde {{\mathsf{A}}}}_{11}{\tilde {{\mathsf{A}}}}_{22} - {\tilde {{\mathsf{A}}}}_{12}{\tilde {{\mathsf{A}}}}_{21}$ can also be obtained. The dynamic equation for
$q = \mathrm {det}( {\tilde {{\mathsf{A}}}}_{ij} ) = {\tilde {{\mathsf{A}}}}_{11}{\tilde {{\mathsf{A}}}}_{22} - {\tilde {{\mathsf{A}}}}_{12}{\tilde {{\mathsf{A}}}}_{21}$ can also be obtained. The dynamic equation for ![]() $p$ is derived by taking the trace of (2.2), i.e.
$p$ is derived by taking the trace of (2.2), i.e.
The dynamic equation for ![]() $q$ can be obtained by multiplying equation (1.1) by
$q$ can be obtained by multiplying equation (1.1) by ![]() ${\mathsf{A}}_{ij}$ and then applying the boundary condition on the free surface as well as the incompressibility condition. This leads to the transport equation for the double product term
${\mathsf{A}}_{ij}$ and then applying the boundary condition on the free surface as well as the incompressibility condition. This leads to the transport equation for the double product term ![]() ${\tilde {{\mathsf{A}}}}_{in}{\tilde {{\mathsf{A}}}}_{nj}$, i.e.
${\tilde {{\mathsf{A}}}}_{in}{\tilde {{\mathsf{A}}}}_{nj}$, i.e.
In this equation, the triple product term ![]() ${\tilde {{\mathsf{A}}}}_{in}{\tilde {{\mathsf{A}}}}_{nk}{\tilde {{\mathsf{A}}}}_{kj}$ can be rewritten using the Cayley–Hamilton theorem,
${\tilde {{\mathsf{A}}}}_{in}{\tilde {{\mathsf{A}}}}_{nk}{\tilde {{\mathsf{A}}}}_{kj}$ can be rewritten using the Cayley–Hamilton theorem, ![]() ${\tilde {{\mathsf{A}}}}_{in}{\tilde {{\mathsf{A}}}}_{nk} + p{\tilde {{\mathsf{A}}}}_{ik} + q\delta _{ik} = 0$, multiplied by
${\tilde {{\mathsf{A}}}}_{in}{\tilde {{\mathsf{A}}}}_{nk} + p{\tilde {{\mathsf{A}}}}_{ik} + q\delta _{ik} = 0$, multiplied by ![]() ${\tilde {{\mathsf{A}}}}_{kj}$ to reduce the triple product term to a double one. Then, taking the trace of the transport equation for
${\tilde {{\mathsf{A}}}}_{kj}$ to reduce the triple product term to a double one. Then, taking the trace of the transport equation for ![]() ${\tilde {{\mathsf{A}}}}_{in}{\tilde {{\mathsf{A}}}}_{nj}$ and eliminating the resulting
${\tilde {{\mathsf{A}}}}_{in}{\tilde {{\mathsf{A}}}}_{nj}$ and eliminating the resulting ![]() ${{\rm d} p}/{{\rm d} t}$ term using (2.3) leads to the dynamic equation for
${{\rm d} p}/{{\rm d} t}$ term using (2.3) leads to the dynamic equation for ![]() $q$:
$q$:
Equations (2.3) and (2.5) form a 2-D nonlinear dynamic system for the evolution of the invariants. It is evident that there is only one fixed point at the origin ![]() $p = q = 0$. Through this fixed point, two manifolds exist and can be expressed as
$p = q = 0$. Through this fixed point, two manifolds exist and can be expressed as
and
The proof of these expressions can be found by comparing the gradient along the manifold, i.e. ![]() ${\rm d} q/ {\rm d} p$ and
${\rm d} q/ {\rm d} p$ and ![]() ${\rm d} q/ {\rm d} p$ calculated by the dynamic system. Evidently, both manifolds exhibit a parabolic form. Moreover,
${\rm d} q/ {\rm d} p$ calculated by the dynamic system. Evidently, both manifolds exhibit a parabolic form. Moreover, ![]() $q = p^{2}/4$ happens to be the boundary across which the eigenvalues of the reduced velocity gradient tensor
$q = p^{2}/4$ happens to be the boundary across which the eigenvalues of the reduced velocity gradient tensor ![]() ${\tilde {{\mathsf{A}}}}_{ij}$ change from complex to real and the local flow topology changes between stable/unstable foci and stable/unstable nodes (see figure 2). As suggested by Cantwell (Reference Cantwell1992), this is coincidental: the factor
${\tilde {{\mathsf{A}}}}_{ij}$ change from complex to real and the local flow topology changes between stable/unstable foci and stable/unstable nodes (see figure 2). As suggested by Cantwell (Reference Cantwell1992), this is coincidental: the factor ![]() $1/3$ in (1.1) is chosen so that the anisotropic pressure Hessian is zero; if a different factor is used, a distinct dynamic system with different manifolds is obtained. We also note that this coincidence is also observed in 3-D turbulence, in which the Vieillefosse tail (figure 1a) also happens to be the boundary that separates the real (corresponding to stable/unstable nodes in 3-D turbulence) and complex (stable/unstable foci) eigenvalues of the velocity gradient tensor.
$1/3$ in (1.1) is chosen so that the anisotropic pressure Hessian is zero; if a different factor is used, a distinct dynamic system with different manifolds is obtained. We also note that this coincidence is also observed in 3-D turbulence, in which the Vieillefosse tail (figure 1a) also happens to be the boundary that separates the real (corresponding to stable/unstable nodes in 3-D turbulence) and complex (stable/unstable foci) eigenvalues of the velocity gradient tensor.

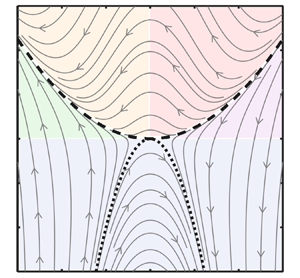
Figure 2. Restricted Euler trajectories (grey lines) calculated based on (2.3) and (2.5). The arrows mark the direction of the trajectories in the phase portrait. The black dashed line and the black dotted line denote the manifolds ![]() $q=p^2/4$ and
$q=p^2/4$ and ![]() $q=-2p^2$, respectively. The shades highlight the local flow topology in each region: stable foci (red); unstable foci (yellow); unstable node (green); saddle (blue); stable node (purple) (Perry & Chong Reference Perry and Chong1987).
$q=-2p^2$, respectively. The shades highlight the local flow topology in each region: stable foci (red); unstable foci (yellow); unstable node (green); saddle (blue); stable node (purple) (Perry & Chong Reference Perry and Chong1987).
It is interesting to examine the stability of these manifolds. For any arbitrary point (![]() $\,p_{0}$,
$\,p_{0}$, ![]() $p_{0}^{2}/4$) located on the first manifold (
$p_{0}^{2}/4$) located on the first manifold (![]() $q = p^{2}/4$), the dynamics is determined by the Jacobian matrix of the dynamic system,
$q = p^{2}/4$), the dynamics is determined by the Jacobian matrix of the dynamic system,
 \begin{equation} \boldsymbol{\mathsf{J}}= \begin{bmatrix}
\dfrac{\partial({\rm d} p/ {\rm d} t)}{\partial p} &
\dfrac{\partial({\rm d} p/ {\rm d} t)}{\partial q}\\
\dfrac{\partial({\rm d} q/ {\rm d} t)}{\partial p} &
\dfrac{\partial({\rm d} q/ {\rm d} t)}{\partial q}
\end{bmatrix}= \begin{bmatrix} -\dfrac{2}{3}p_0 &
-\dfrac{2}{3} \\ -\dfrac{19}{12}p_0^2 & \dfrac{5}{3}p_0
\end{bmatrix}. \end{equation}
\begin{equation} \boldsymbol{\mathsf{J}}= \begin{bmatrix}
\dfrac{\partial({\rm d} p/ {\rm d} t)}{\partial p} &
\dfrac{\partial({\rm d} p/ {\rm d} t)}{\partial q}\\
\dfrac{\partial({\rm d} q/ {\rm d} t)}{\partial p} &
\dfrac{\partial({\rm d} q/ {\rm d} t)}{\partial q}
\end{bmatrix}= \begin{bmatrix} -\dfrac{2}{3}p_0 &
-\dfrac{2}{3} \\ -\dfrac{19}{12}p_0^2 & \dfrac{5}{3}p_0
\end{bmatrix}. \end{equation}
We then examine the stability of this point along the normal direction with respect to the manifold, which is determined by calculating the term ![]() ${\hat {e}}_{\bot i}{\mathsf{J}}_{ij}{\hat {e}}_{\bot j}$, where
${\hat {e}}_{\bot i}{\mathsf{J}}_{ij}{\hat {e}}_{\bot j}$, where ![]() ${\hat {e}}_{\bot i}$ is the unit vector normal to the same manifold. The condition
${\hat {e}}_{\bot i}$ is the unit vector normal to the same manifold. The condition ![]() ${\hat {e}}_{\bot i}{\mathsf{J}}_{ij}{\hat {e}}_{\bot j} > 0$ implies that (
${\hat {e}}_{\bot i}{\mathsf{J}}_{ij}{\hat {e}}_{\bot j} > 0$ implies that (![]() $\,p_{0}$,
$\,p_{0}$, ![]() $p_{0}^{2}/4$) is unstable, and vice versa. By substituting
$p_{0}^{2}/4$) is unstable, and vice versa. By substituting ![]() $q = p^{2}/4$ into
$q = p^{2}/4$ into ![]() ${\hat {e}}_{\bot i}{\mathsf{J}}_{ij}{\hat {e}}_{\bot j}$, we can write
${\hat {e}}_{\bot i}{\mathsf{J}}_{ij}{\hat {e}}_{\bot j}$, we can write ![]() ${\hat {e}}_{\bot i}{\mathsf{J}}_{ij}{\hat {e}}_{\bot j} = {( 5p_{0}^{2} + 16 )( {2p}_{0}^{2} + 8 )^{- 1}p}_{0}$. Evidently, the sign of
${\hat {e}}_{\bot i}{\mathsf{J}}_{ij}{\hat {e}}_{\bot j} = {( 5p_{0}^{2} + 16 )( {2p}_{0}^{2} + 8 )^{- 1}p}_{0}$. Evidently, the sign of ![]() ${\hat {e}}_{\bot i}{\mathsf{J}}_{ij}{\hat {e}}_{\bot j}$ is consistent with the sign of
${\hat {e}}_{\bot i}{\mathsf{J}}_{ij}{\hat {e}}_{\bot j}$ is consistent with the sign of ![]() $p_{0}$. This indicates that the first manifold (
$p_{0}$. This indicates that the first manifold (![]() $q = p^{2}/4$) is unstable for
$q = p^{2}/4$) is unstable for ![]() $p > 0$ and stable for
$p > 0$ and stable for ![]() $p < 0$. A similar analysis can be conducted for the other manifold
$p < 0$. A similar analysis can be conducted for the other manifold ![]() $q = - 2p^{2}$, and one can write
$q = - 2p^{2}$, and one can write ![]() ${\hat {e}}_{\bot i}{\mathsf{J}}_{ij}{\hat {e}}_{\bot j} = - ( 32p_{0}^{2} + 1 )( 16p_{0}^{2} + 1 )^{- 1}p_{0}$. The sign of
${\hat {e}}_{\bot i}{\mathsf{J}}_{ij}{\hat {e}}_{\bot j} = - ( 32p_{0}^{2} + 1 )( 16p_{0}^{2} + 1 )^{- 1}p_{0}$. The sign of ![]() ${\hat {e}}_{\bot i}{\mathsf{J}}_{ij}{\hat {e}}_{\bot j}$ is opposite to the sign of
${\hat {e}}_{\bot i}{\mathsf{J}}_{ij}{\hat {e}}_{\bot j}$ is opposite to the sign of ![]() $p_{0}$, suggesting that this manifold is stable for
$p_{0}$, suggesting that this manifold is stable for ![]() $p > 0$ while is unstable for
$p > 0$ while is unstable for ![]() $p < 0$.
$p < 0$.
Figure 2 shows the ![]() $p$–
$p$–![]() $q$ phase portrait based on the restricted Euler model calculated numerically from (2.3) and (2.5). The arrows indicate the directions in which the system evolves. Also shown are the two manifold
$q$ phase portrait based on the restricted Euler model calculated numerically from (2.3) and (2.5). The arrows indicate the directions in which the system evolves. Also shown are the two manifold ![]() $q = p^{2}/4$ and
$q = p^{2}/4$ and ![]() $q = - 2p^{2}$. The trajectories above the parabola
$q = - 2p^{2}$. The trajectories above the parabola ![]() $q = p^{2}/4$ are directed from right to left with a bump around the axis
$q = p^{2}/4$ are directed from right to left with a bump around the axis ![]() $p = 0$, and move from left to right below the parabola
$p = 0$, and move from left to right below the parabola ![]() $q = - 2p^{2}$. The stability properties of the manifolds are evident by recognizing that the trajectories are directed towards or away from the manifolds depending on the sign of
$q = - 2p^{2}$. The stability properties of the manifolds are evident by recognizing that the trajectories are directed towards or away from the manifolds depending on the sign of ![]() $p$, consistent with the analysis presented above. The phase portrait also suggests that all initial conditions will eventually proceed to a finite-time singularity along either the left-hand branch of
$p$, consistent with the analysis presented above. The phase portrait also suggests that all initial conditions will eventually proceed to a finite-time singularity along either the left-hand branch of ![]() $q = p^{2}/4$ or the right-hand branch of
$q = p^{2}/4$ or the right-hand branch of ![]() $q = - 2p^{2}$. This finite-time singularity along
$q = - 2p^{2}$. This finite-time singularity along ![]() $q=p^2/4$ corresponds to the same singularity along the Vieillefosse tail in 3-D turbulence (see figure 1a) and thus they represent the same physical flow topology with different mathematical manifestations. The presence of finite-time singularities implies that
$q=p^2/4$ corresponds to the same singularity along the Vieillefosse tail in 3-D turbulence (see figure 1a) and thus they represent the same physical flow topology with different mathematical manifestations. The presence of finite-time singularities implies that ![]() $p$ and
$p$ and ![]() $q$, as well as
$q$, as well as ![]() ${\tilde {{\mathsf{A}}}}_{ij}$, will eventually approach infinity via a process of gradient self-amplification, as in 3-D turbulence (Meneveau Reference Meneveau2011; Johnson & Wilczek Reference Johnson and Wilczek2024). In real flows, viscosity and the pressure Hessian will prevent diverging values of the velocity gradient. However, the presence of two manifolds associated with finite-time singularities suggests that extremely large values of velocity gradients are relatively likely, even more so than in 3-D turbulence. Indeed, simulations by Eckhardt & Schumacher (Reference Eckhardt and Schumacher2001) and measurements by Li et al. (Reference Li, Wang, Qi and Coletti2024) emphasized how free-surface turbulence is characterized by stronger intermittency than 3-D turbulence.
${\tilde {{\mathsf{A}}}}_{ij}$, will eventually approach infinity via a process of gradient self-amplification, as in 3-D turbulence (Meneveau Reference Meneveau2011; Johnson & Wilczek Reference Johnson and Wilczek2024). In real flows, viscosity and the pressure Hessian will prevent diverging values of the velocity gradient. However, the presence of two manifolds associated with finite-time singularities suggests that extremely large values of velocity gradients are relatively likely, even more so than in 3-D turbulence. Indeed, simulations by Eckhardt & Schumacher (Reference Eckhardt and Schumacher2001) and measurements by Li et al. (Reference Li, Wang, Qi and Coletti2024) emphasized how free-surface turbulence is characterized by stronger intermittency than 3-D turbulence.
The ![]() $p$–
$p$–![]() $q$ phase portrait also predicts how the topology of the local velocity field evolves over time. As illustrated by the schematic and shade in figure 2, it can be seen that stable foci above
$q$ phase portrait also predicts how the topology of the local velocity field evolves over time. As illustrated by the schematic and shade in figure 2, it can be seen that stable foci above ![]() $q = p^{2}/4$ in the first quadrant will evolve towards unstable foci. This is consistent with the dynamics in the 3-D restricted Euler system (see figure 1a) in which stable foci also evolve into unstable foci governed by
$q = p^{2}/4$ in the first quadrant will evolve towards unstable foci. This is consistent with the dynamics in the 3-D restricted Euler system (see figure 1a) in which stable foci also evolve into unstable foci governed by ![]() ${\rm d} R/ {\rm d} t=(2/3)Q^2\geq 0$. Stable nodes below
${\rm d} R/ {\rm d} t=(2/3)Q^2\geq 0$. Stable nodes below ![]() $q = p^{2}/4$ in the first quadrant will become saddles, while unstable nodes can only evolve from saddles. Saddles below
$q = p^{2}/4$ in the first quadrant will become saddles, while unstable nodes can only evolve from saddles. Saddles below ![]() $q = - 2p^{2}$ remain such, thus their topology does not significantly change. These behaviours correspond to the intermediate eigenvalue of the three real eigenvalues of the full velocity gradient tensor changing from negative to positive, again equivalent to the dynamics in the 3-D restricted Euler system. We emphasize that this insight on the flow topology is based on the restricted Euler model in which the effects of viscosity and anisotropic pressure Hessian are removed.
$q = - 2p^{2}$ remain such, thus their topology does not significantly change. These behaviours correspond to the intermediate eigenvalue of the three real eigenvalues of the full velocity gradient tensor changing from negative to positive, again equivalent to the dynamics in the 3-D restricted Euler system. We emphasize that this insight on the flow topology is based on the restricted Euler model in which the effects of viscosity and anisotropic pressure Hessian are removed.
3. Experimental set-up and results
To verify the prediction of the restricted Euler dynamics in free surface turbulence, we present results from experiments conducted in a turbulent water tank of dimensions ![]() $2 \times 1 \times 1 {\rm m}^3$, illustrated in figure 3(a). Two
$2 \times 1 \times 1 {\rm m}^3$, illustrated in figure 3(a). Two ![]() $8 \times 8$ arrays of submerged pumps facing each other generate homogeneous turbulence in the centre of the tank over a region of approximately (0.5 m)
$8 \times 8$ arrays of submerged pumps facing each other generate homogeneous turbulence in the centre of the tank over a region of approximately (0.5 m)![]() $^3$. Details regarding this facility can be found in Ruth & Coletti (Reference Ruth and Coletti2024) and Li et al. (Reference Li, Wang, Qi and Coletti2024). The intensity of the velocity fluctuations
$^3$. Details regarding this facility can be found in Ruth & Coletti (Reference Ruth and Coletti2024) and Li et al. (Reference Li, Wang, Qi and Coletti2024). The intensity of the velocity fluctuations ![]() $u_{rms}$ and the dissipation rate of the turbulent kinetic energy
$u_{rms}$ and the dissipation rate of the turbulent kinetic energy ![]() $\epsilon$ are varied in the range
$\epsilon$ are varied in the range ![]() $u_{rms} = 0.02$ to 0.03 m s
$u_{rms} = 0.02$ to 0.03 m s![]() $^{-1}$ and
$^{-1}$ and ![]() $\epsilon = 3.82 \times 10^{- 5}$ to
$\epsilon = 3.82 \times 10^{- 5}$ to ![]() $2.21 \times 10^{- 4}\ {\rm m}^{2}\ {\rm s}^{-3}$ by changing the power supplied to each pump. This leads to a range of Taylor Reynolds number
$2.21 \times 10^{- 4}\ {\rm m}^{2}\ {\rm s}^{-3}$ by changing the power supplied to each pump. This leads to a range of Taylor Reynolds number ![]() $Re_{\lambda } = 207$ to
$Re_{\lambda } = 207$ to ![]() $312$. We note that strong surface deformation due to the subsurface turbulence could bring difficulties and large uncertainty in the surface velocity measurement. However, in this regime, the surface remains essentially flat, with only submillimetre deformations due to the subsurface turbulence. Therefore, such surface deformation is neglected and will not significantly affect the result.
$312$. We note that strong surface deformation due to the subsurface turbulence could bring difficulties and large uncertainty in the surface velocity measurement. However, in this regime, the surface remains essentially flat, with only submillimetre deformations due to the subsurface turbulence. Therefore, such surface deformation is neglected and will not significantly affect the result.

Figure 3. (a) A schematic of the turbulent water tank and camera arrangement. The green shaded area represents the field of view (FOV). (b) A snapshot of particle trajectories on the free surface in the FOV at ![]() $Re_{\lambda } = 312$. The trajectories are colour coded by the velocity magnitude.
$Re_{\lambda } = 312$. The trajectories are colour coded by the velocity magnitude.
The free surface of the water is maintained at 8 cm above the axis of the jets at the top row of the arrays. As depicted in figure 3(a), the surface motion is captured by a downward looking CMOS camera placed approximately 0.31 m above the surface. This is operated at 400 f.p.s., with a resolution of ![]() $1664 \times 1600$ pixels over a
$1664 \times 1600$ pixels over a ![]() $10 \times 10\ {\rm cm}^{2}$ FOV illuminated by two light-emitting diode panels. To resolve the small-scale dynamics, the surface motion is characterized by tracking floating hollow glass microspheres (63–75
$10 \times 10\ {\rm cm}^{2}$ FOV illuminated by two light-emitting diode panels. To resolve the small-scale dynamics, the surface motion is characterized by tracking floating hollow glass microspheres (63–75 ![]() $\mathrm {\mu }$m in diameter and 0.31 g cm
$\mathrm {\mu }$m in diameter and 0.31 g cm![]() $^{-3}$ in density), at a high concentration approximately 120 particles cm
$^{-3}$ in density), at a high concentration approximately 120 particles cm![]() $^{-2}$. Individual particles are identified and tracked via an in-house particle tracking velocimetry (PTV) code based on the nearest-neighbour algorithm (Petersen, Baker & Coletti Reference Petersen, Baker and Coletti2019). The velocity is obtained by convolving the trajectories with the first derivative of a temporal Gaussian kernel, whose width is comparable to the smallest time scales of the flow (Mordant, Crawford & Bodenschatz Reference Mordant, Crawford and Bodenschatz2004a). Figure 3(b) shows an example of trajectories obtained over a series of 25 successive images.
$^{-2}$. Individual particles are identified and tracked via an in-house particle tracking velocimetry (PTV) code based on the nearest-neighbour algorithm (Petersen, Baker & Coletti Reference Petersen, Baker and Coletti2019). The velocity is obtained by convolving the trajectories with the first derivative of a temporal Gaussian kernel, whose width is comparable to the smallest time scales of the flow (Mordant, Crawford & Bodenschatz Reference Mordant, Crawford and Bodenschatz2004a). Figure 3(b) shows an example of trajectories obtained over a series of 25 successive images.
The reduced velocity gradient tensor ![]() ${\tilde {{\mathsf{A}}}}_{ij}$ at each particle position on the free surface is obtained by performing a least-square fit based on the velocity of particles within a search radius
${\tilde {{\mathsf{A}}}}_{ij}$ at each particle position on the free surface is obtained by performing a least-square fit based on the velocity of particles within a search radius ![]() $R_{s}$ (Pumir, Bodenschatz & Xu Reference Pumir, Bodenschatz and Xu2013; Qi et al. Reference Qi, Tan, Corbitt, Urbanik, Salibindla and Ni2022). When
$R_{s}$ (Pumir, Bodenschatz & Xu Reference Pumir, Bodenschatz and Xu2013; Qi et al. Reference Qi, Tan, Corbitt, Urbanik, Salibindla and Ni2022). When ![]() $R_{s}$ is large, the calculated velocity gradient will be coarse-grained; while small
$R_{s}$ is large, the calculated velocity gradient will be coarse-grained; while small ![]() $R_{s}$ leads to a limited number of surrounding particles, thus larger uncertainty. The value is thus determined following an approach similar to the one for the PTV kernel (Mordant et al. Reference Mordant, Crawford and Bodenschatz2004a):
$R_{s}$ leads to a limited number of surrounding particles, thus larger uncertainty. The value is thus determined following an approach similar to the one for the PTV kernel (Mordant et al. Reference Mordant, Crawford and Bodenschatz2004a): ![]() $R_{s}$ is chosen as the smallest value above which the standard deviation of
$R_{s}$ is chosen as the smallest value above which the standard deviation of ![]() ${\tilde {{\mathsf{A}}}}_{ij}$ decays exponentially with it. Following this approach,
${\tilde {{\mathsf{A}}}}_{ij}$ decays exponentially with it. Following this approach, ![]() $R_{s} = 2.5$ mm is used which yields on average 40 particles within the search radius. This
$R_{s} = 2.5$ mm is used which yields on average 40 particles within the search radius. This ![]() $R_s$ is comparable to the Kolmogorov length scale defined on the free surface and the results are insensitive to the precise value of the search radius. More details can be found in Qi, Li & Coletti (Reference Qi, Li and Coletti2024).
$R_s$ is comparable to the Kolmogorov length scale defined on the free surface and the results are insensitive to the precise value of the search radius. More details can be found in Qi, Li & Coletti (Reference Qi, Li and Coletti2024).
With ![]() ${\tilde {{\mathsf{A}}}}_{ij}$ obtained from the experiment, the invariants
${\tilde {{\mathsf{A}}}}_{ij}$ obtained from the experiment, the invariants ![]() $p$ and
$p$ and ![]() $q$ are calculated and their joint p.d.f.s are shown in figure 4(a) for
$q$ are calculated and their joint p.d.f.s are shown in figure 4(a) for ![]() $Re_{\lambda } = 312$. Both invariants are normalized by the vorticity of the surface flow,
$Re_{\lambda } = 312$. Both invariants are normalized by the vorticity of the surface flow, ![]() $\omega = {\tilde {{\mathsf{A}}}}_{21} - {\tilde {{\mathsf{A}}}}_{12}$. The dashed line and dotted line mark the manifolds
$\omega = {\tilde {{\mathsf{A}}}}_{21} - {\tilde {{\mathsf{A}}}}_{12}$. The dashed line and dotted line mark the manifolds ![]() $q = p^{2}/4$ and
$q = p^{2}/4$ and ![]() $q = - 2p^{2}$ obtained from the reduced Euler representation. We note the distribution of the joint p.d.f. does not change significantly between various cases. Thus, the following discussion should apply for at least the Reynolds number range considered in this work.
$q = - 2p^{2}$ obtained from the reduced Euler representation. We note the distribution of the joint p.d.f. does not change significantly between various cases. Thus, the following discussion should apply for at least the Reynolds number range considered in this work.

Figure 4. (a) The joint p.d.f. of normalized ![]() $p$ and
$p$ and ![]() $q$ at
$q$ at ![]() $Re_{\lambda } = 312$ based on the experimental data. The logarithmic contours range from
$Re_{\lambda } = 312$ based on the experimental data. The logarithmic contours range from ![]() $10^{- 7}$ to
$10^{- 7}$ to ![]() $10$ with adjacent contours being separated by half a decade. (b) The initial joint p.d.f. of normalized
$10$ with adjacent contours being separated by half a decade. (b) The initial joint p.d.f. of normalized ![]() $p$ and
$p$ and ![]() $q$ for the Monte Carlo simulation. (c) The joint p.d.f. of normalized
$q$ for the Monte Carlo simulation. (c) The joint p.d.f. of normalized ![]() $p$ and
$p$ and ![]() $q$ obtained from the Monte Carlo simulation at
$q$ obtained from the Monte Carlo simulation at ![]() $\langle \omega ^2\rangle ^{1/2} t=0.15$. For (b,c), the logarithmic contours range from
$\langle \omega ^2\rangle ^{1/2} t=0.15$. For (b,c), the logarithmic contours range from ![]() $10^{- 6}$ to
$10^{- 6}$ to ![]() $1$ with adjacent contours being separated by half a decade. In all the three panels, the white dashed lines mark
$1$ with adjacent contours being separated by half a decade. In all the three panels, the white dashed lines mark ![]() $q = p^{2}/4$, and white dotted lines mark
$q = p^{2}/4$, and white dotted lines mark ![]() $q = - 2p^{2}$.
$q = - 2p^{2}$.
Remarkably, the contours in the ![]() $p$–
$p$–![]() $q$ joint p.d.f. show similarities with the trajectories in the analytical phase portrait shown in figure 2. In particular, a relatively high probability is found along the manifold
$q$ joint p.d.f. show similarities with the trajectories in the analytical phase portrait shown in figure 2. In particular, a relatively high probability is found along the manifold ![]() $q = p^{2}/4$, especially its left branch, highlighting the role of strain self-amplification which results in exceptionally strong intermittency. Quantitatively, the kurtosis of the velocity gradients along the surface (
$q = p^{2}/4$, especially its left branch, highlighting the role of strain self-amplification which results in exceptionally strong intermittency. Quantitatively, the kurtosis of the velocity gradients along the surface (![]() $\tilde {{\mathsf{A}}}_{11}$) is approximately 9.5, which is higher than the one for 3-D homogeneous turbulence at similar
$\tilde {{\mathsf{A}}}_{11}$) is approximately 9.5, which is higher than the one for 3-D homogeneous turbulence at similar ![]() $Re_\lambda$ (Gylfason, Ayyalasomayajula & Warhaft Reference Gylfason, Ayyalasomayajula and Warhaft2004). The asymmetry of the distribution reflects the stability properties of this manifold, i.e. the left-hand branch is stable as discussed above and thus exhibits higher probability. Although the manifold
$Re_\lambda$ (Gylfason, Ayyalasomayajula & Warhaft Reference Gylfason, Ayyalasomayajula and Warhaft2004). The asymmetry of the distribution reflects the stability properties of this manifold, i.e. the left-hand branch is stable as discussed above and thus exhibits higher probability. Although the manifold ![]() $q = - 2p^{2}$ does not leave an obvious footprint, the relatively higher probability in the fourth quadrant than the one in the third quadrant is consistent with the stability of its right-hand branch. The fact that no clear tail is observed along this manifold still requires further investigation.
$q = - 2p^{2}$ does not leave an obvious footprint, the relatively higher probability in the fourth quadrant than the one in the third quadrant is consistent with the stability of its right-hand branch. The fact that no clear tail is observed along this manifold still requires further investigation.
To better compare the joint p.d.f. with the restricted Euler model, a Monte Carlo simulation is performed. A large ensemble of ![]() $O(10^7)$ initial sets of invariants is considered and each of these sets is evolved following (2.3) and (2.5). The initial values of invariants are obtained from the reduced velocity gradient tensor, each element of which follows a Gaussian distribution with the same variance and zero mean, as illustrated in figure 4(b). We note that as the restricted Euler system is divergent, the predicted joint p.d.f. does not converge to a statistically stationary state. Thus, in figure 4(c), the predicted joint p.d.f. at an intermediate time instant (
$O(10^7)$ initial sets of invariants is considered and each of these sets is evolved following (2.3) and (2.5). The initial values of invariants are obtained from the reduced velocity gradient tensor, each element of which follows a Gaussian distribution with the same variance and zero mean, as illustrated in figure 4(b). We note that as the restricted Euler system is divergent, the predicted joint p.d.f. does not converge to a statistically stationary state. Thus, in figure 4(c), the predicted joint p.d.f. at an intermediate time instant (![]() $\langle \omega ^2\rangle ^{1/2} t=0.15$, where
$\langle \omega ^2\rangle ^{1/2} t=0.15$, where ![]() $t$ indicates time) is used to compare with the experimental data, though the features remain qualitatively similar at different times.
$t$ indicates time) is used to compare with the experimental data, though the features remain qualitatively similar at different times.
In figure 4, large deviations between the experimental and the predicted joint p.d.f. are evident, in particular the high probability around ![]() $p=0$ in the former. This is associated with low levels of the compressibility ratio
$p=0$ in the former. This is associated with low levels of the compressibility ratio ![]() $\mathcal {C}=\langle (\tilde {{\mathsf{A}}}_{ii})^2 \rangle /\langle (\tilde {{\mathsf{A}}}_{ij})^2\rangle =0.013$–
$\mathcal {C}=\langle (\tilde {{\mathsf{A}}}_{ii})^2 \rangle /\langle (\tilde {{\mathsf{A}}}_{ij})^2\rangle =0.013$–![]() $0.024$ found in the measurements. This is much lower than
$0.024$ found in the measurements. This is much lower than ![]() $\mathcal {C}=0.45$–
$\mathcal {C}=0.45$–![]() $0.5$ observed by Cressman et al. (Reference Cressman, Davoudi, Goldburg and Schumacher2004) who forced turbulence at a much deeper distance under the free surface with
$0.5$ observed by Cressman et al. (Reference Cressman, Davoudi, Goldburg and Schumacher2004) who forced turbulence at a much deeper distance under the free surface with ![]() $Re_\lambda =100$–
$Re_\lambda =100$–![]() $140$. It is possible that differences in the details of the forcing scheme impact the state of the surface flow. We note, however, that the compressibility ratio we measure is largely unaffected by changing the depth of the forcing. Despite the large deviations, the predicted joint p.d.f. still successfully reproduces some features of the experimental data; in particular, the higher probability along the left-hand branch of
$140$. It is possible that differences in the details of the forcing scheme impact the state of the surface flow. We note, however, that the compressibility ratio we measure is largely unaffected by changing the depth of the forcing. Despite the large deviations, the predicted joint p.d.f. still successfully reproduces some features of the experimental data; in particular, the higher probability along the left-hand branch of ![]() $q=p^2/4$ and the slightly higher probability in the fourth quadrant than the one in the third quadrant. The manifold
$q=p^2/4$ and the slightly higher probability in the fourth quadrant than the one in the third quadrant. The manifold ![]() $q=-2p^2$ does not show a clear footprint as in the experimental data, indicating that this manifold might not affect the dynamics of the reduced velocity gradient as much as the manifold
$q=-2p^2$ does not show a clear footprint as in the experimental data, indicating that this manifold might not affect the dynamics of the reduced velocity gradient as much as the manifold ![]() $q=p^2/4$.
$q=p^2/4$.
Given the asymmetry observed in the measured joint p.d.f. (figure 4a), it is informative to examine the mean of both invariants. As the gradients of the mean velocity components are weak (Li et al. Reference Li, Wang, Qi and Coletti2024), the average of ![]() $p$ is expected to be approximately zero
$p$ is expected to be approximately zero ![]() $\langle \,p\rangle = - \partial \langle u_1\rangle /\partial x_1 - \partial \langle u_2\rangle /\partial x_2 = 0$. In addition, given the homogeneity of the free-surface turbulence, the cross product of velocity gradient also satisfies
$\langle \,p\rangle = - \partial \langle u_1\rangle /\partial x_1 - \partial \langle u_2\rangle /\partial x_2 = 0$. In addition, given the homogeneity of the free-surface turbulence, the cross product of velocity gradient also satisfies ![]() $\langle (\partial u_1/\partial x_1) (\partial u_2/\partial x_2)\rangle = \langle (\partial u_1/\partial x_2)(\partial u_2/\partial x_1)\rangle$ (George & Hussein Reference George and Hussein1991). Substituting this relation into the definition of
$\langle (\partial u_1/\partial x_1) (\partial u_2/\partial x_2)\rangle = \langle (\partial u_1/\partial x_2)(\partial u_2/\partial x_1)\rangle$ (George & Hussein Reference George and Hussein1991). Substituting this relation into the definition of ![]() $q$ results in
$q$ results in ![]() $\langle q\rangle = \langle (\partial u_1/\partial x_1)(\partial u_2/\partial x_2)\rangle - \langle (\partial u_1/\partial x_2)(\partial u_2/\partial x_1)\rangle = 0$. Therefore, both invariants are expected to have zero mean,
$\langle q\rangle = \langle (\partial u_1/\partial x_1)(\partial u_2/\partial x_2)\rangle - \langle (\partial u_1/\partial x_2)(\partial u_2/\partial x_1)\rangle = 0$. Therefore, both invariants are expected to have zero mean, ![]() $\langle p\rangle = \langle q\rangle = 0$. This is approximately confirmed by the present data, which gives
$\langle p\rangle = \langle q\rangle = 0$. This is approximately confirmed by the present data, which gives ![]() $\langle p \rangle /\langle \omega ^{2} \rangle ^{1/2} = 1.7 \times 10^{- 3}$ and
$\langle p \rangle /\langle \omega ^{2} \rangle ^{1/2} = 1.7 \times 10^{- 3}$ and ![]() $\langle q \rangle /\langle \omega ^{2} \rangle = - 0.035$.
$\langle q \rangle /\langle \omega ^{2} \rangle = - 0.035$.
It is also noted that the joint p.d.f. of invariants (figure 4a) displays a distinct pattern from the one obtained from generic 2-D sections of 3-D turbulence (Cardesa et al. Reference Cardesa, Mistry, Gan and Dawson2013). The teapot shape (as in figure 1c) shows a much more pronounced asymmetry compared with the present free-surface case. This asymmetry, quantified by the inequality ![]() $\langle pq \rangle < 0$, is found to be connected to the predominance of vortex stretching over vortex compression in 3-D turbulence. In particular, they found that
$\langle pq \rangle < 0$, is found to be connected to the predominance of vortex stretching over vortex compression in 3-D turbulence. In particular, they found that ![]() $\langle pq \rangle /\langle \omega ^2 \rangle ^{3/2}$ ranged between
$\langle pq \rangle /\langle \omega ^2 \rangle ^{3/2}$ ranged between ![]() $-0.044$ and
$-0.044$ and ![]() $-0.067$ for 3-D turbulence, while in the present case we measure
$-0.067$ for 3-D turbulence, while in the present case we measure ![]() $\langle pq \rangle /\langle \omega ^2 \rangle ^{3/2} = - 1.8 \times 10^{- 3}$. Therefore, we deduce that the weaker asymmetry observed here is due to the no-shear-stress boundary condition which eliminates the vortex stretching along the free-surface directions. This is crucial for the dynamics, as vortex stretching is a major factor in the interscale energy transfer in 3-D turbulence (Davidson Reference Davidson2015; Johnson Reference Johnson2020, Reference Johnson2021). This may have far-reaching consequences for the energy cascade associated with the dynamics along the free surface, which has been found to exhibit inverse interscale fluxes from scales small to large (Pan & Banerjee Reference Pan and Banerjee1995; Lovecchio, Zonta & Soldati Reference Lovecchio, Zonta and Soldati2015). Moreover, surface-attached vortices are linked to surface-divergence events (Babiker et al. Reference Babiker, Bjerkebæk, Xuan, Shen and Ellingsen2023) which are crucial for gas transfer to and from the liquid (Jähne & Haußecker Reference Jähne and Haußecker1998; Herlina & Wissink Reference Herlina and Wissink2019). Inspired by these considerations, further studies are warranted to conduct a complete description of the surface flow topology and dynamics.
$\langle pq \rangle /\langle \omega ^2 \rangle ^{3/2} = - 1.8 \times 10^{- 3}$. Therefore, we deduce that the weaker asymmetry observed here is due to the no-shear-stress boundary condition which eliminates the vortex stretching along the free-surface directions. This is crucial for the dynamics, as vortex stretching is a major factor in the interscale energy transfer in 3-D turbulence (Davidson Reference Davidson2015; Johnson Reference Johnson2020, Reference Johnson2021). This may have far-reaching consequences for the energy cascade associated with the dynamics along the free surface, which has been found to exhibit inverse interscale fluxes from scales small to large (Pan & Banerjee Reference Pan and Banerjee1995; Lovecchio, Zonta & Soldati Reference Lovecchio, Zonta and Soldati2015). Moreover, surface-attached vortices are linked to surface-divergence events (Babiker et al. Reference Babiker, Bjerkebæk, Xuan, Shen and Ellingsen2023) which are crucial for gas transfer to and from the liquid (Jähne & Haußecker Reference Jähne and Haußecker1998; Herlina & Wissink Reference Herlina and Wissink2019). Inspired by these considerations, further studies are warranted to conduct a complete description of the surface flow topology and dynamics.
4. Conclusion
In this work, we have developed a restricted Euler model for the reduced velocity gradient tensor in free-surface turbulence by simplifying the 3-D restricted Euler model using free-surface boundary conditions. Two manifolds associated with finite-time singularities appear in the phase portrait that describes the dynamics of the invariants ![]() $p$ and
$p$ and ![]() $q$, highlighting the intrinsic intermittent nature of
$q$, highlighting the intrinsic intermittent nature of ![]() ${\tilde {{\mathsf{A}}}}_{ij}$. The model is compared with experimental data obtained in a turbulent water tank with quasiflat free surface, in which the surface velocity gradient is obtained by tracking highly concentrated floating microspheres. The
${\tilde {{\mathsf{A}}}}_{ij}$. The model is compared with experimental data obtained in a turbulent water tank with quasiflat free surface, in which the surface velocity gradient is obtained by tracking highly concentrated floating microspheres. The ![]() $p$–
$p$–![]() $q$ joint p.d.f. shows a distinct pattern which differs significantly from the one measured in 2-D sections of 3-D turbulence. Some features of the joint p.d.f., including the high probability along the unstable branch of
$q$ joint p.d.f. shows a distinct pattern which differs significantly from the one measured in 2-D sections of 3-D turbulence. Some features of the joint p.d.f., including the high probability along the unstable branch of ![]() $q=p^2/4$ and the asymmetry of the distribution, are predicted by the restricted Euler model. This study provides experimental evidence as well as a theoretical basis for the enhanced intermittency in free-surface turbulence.
$q=p^2/4$ and the asymmetry of the distribution, are predicted by the restricted Euler model. This study provides experimental evidence as well as a theoretical basis for the enhanced intermittency in free-surface turbulence.
Despite the success of the current model in predicting certain features, large deviations between the experimental and predicted joint p.d.f.s are evident, particularly the high probability around ![]() $p=0$, associated with a weak surface compressibility observed in the experiments which deserves further investigation. In addition, the magnitude of the skewness is greatly overpredicted. We remark that the current model is inherently not convergent (i.e. does not reach a steady state) due to the lack of pressure Hessian and viscous effect. Further improvements of the model to take into account these terms are needed to guarantee convergent and more accurate predictions, and to advance the understanding on the evolution of the reduced velocity gradient tensor on the free surface.
$p=0$, associated with a weak surface compressibility observed in the experiments which deserves further investigation. In addition, the magnitude of the skewness is greatly overpredicted. We remark that the current model is inherently not convergent (i.e. does not reach a steady state) due to the lack of pressure Hessian and viscous effect. Further improvements of the model to take into account these terms are needed to guarantee convergent and more accurate predictions, and to advance the understanding on the evolution of the reduced velocity gradient tensor on the free surface.
Funding
Funding from the Swiss National Science Foundation (project no. 200021-207318) is gratefully acknowledged.
Declaration of interests
The authors report no conflict of interest.
Data availability statement
All the data supporting this work are available from the corresponding author upon reasonable request.