Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2025-01-02T20:40:35.541Z Has data issue: false hasContentIssue false
  • English
  • Français

Response of a hypersonic turbulent boundary layer to favourable pressure gradients

Published online by Cambridge University Press:  28 March 2013

N. R. Tichenor ,
R. A. Humble  and
R. D. W. Bowersox
N. R. Tichenor*
Affiliation:
Physics, Materials and Applied Mathematics Research, L.L.C., Tucson, AZ 85719, USA
R. A. Humble
Affiliation:
Department of Aerospace Engineering, Texas A&M University, College Station, TX 77843-3141, USA
R. D. W. Bowersox
Affiliation:
Department of Aerospace Engineering, Texas A&M University, College Station, TX 77843-3141, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The role of streamline curvature-driven favourable pressure gradients in modifying the turbulence structure of a Mach 4.9, high-Reynolds-number (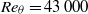${\mathit{Re}}_{\theta } = 43\hspace{0.167em} 000$) boundary layer is examined. Three pressure gradient cases (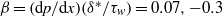$\beta = (\mathrm{d} p/ \mathrm{d} x)({\delta }^{\ast } / {\tau }_{w} )= 0. 07, - 0. 3$ and 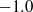$- 1. 0$) are characterized via particle image velocimetry. The expected stabilizing trends in the Reynolds stresses are observed, with a sign reversal in the Reynolds shear stress in the outer part of the boundary layer for the strongest favourable pressure gradient considered. The increased transverse normal strain rate and reduced principal strain rate are the primary factors. Reynolds stress quadrant events are redistributed, such that the relative differences between the quadrant magnitudes decreases. Very little preferential quadrant mode selection is observed for the strongest pressure gradient considered. Two-point correlations suggest that the turbulent structures are reoriented to lean farther away from the wall, accompanied by a slight reduction in their characteristic size, consistent with previous flow visualization studies. This reorientation is more pronounced in the outer, dilatation-dominated region of the boundary layer, whereas the alteration in structure size is more pronounced nearer the wall, where the principal strain rates are larger. In addition, integration of a simplified form of a Reynolds stress transport closure model provided a framework to assess the role of the strain-rate field on the observed Reynolds shear stresses. Given the simple geometry, the present data provide a suitable test bed for Reynolds stress transport and large-eddy model development and validation.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 722 , 10 May 2013 , pp. 187 - 213
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R., Meinhart, C. & Tomkins, C. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Arnette, S., Samimy, M. & Elliott, G. 1995 Structure of supersonic turbulent boundary layer after expansion regions. AIAA J. 33 (3), 430–438.CrossRefGoogle Scholar
Arnette, S., Samimy, M. & Elliott, G. 1998 The effects of expansion on the turbulence structure of compressible boundary layers. J. Fluid Mech. 367, 67–105.CrossRefGoogle Scholar
Benedict, L. & Gould, R. 1996 Towards better uncertainty estimates for turbulence statistics. Exp. Fluids 22, 129–136.CrossRefGoogle Scholar
Bradshaw, P. 1969 The analogy between streamline curvature and buoyancy in turbulent shear flow. J. Fluid Mech. 36, 177–191.CrossRefGoogle Scholar
Bradshaw, P. 1973 The effect of streamline curvature on turbulent flow. AGARDograph 169.Google Scholar
Bradshaw, P. 1974 The effect of mean compression or dilatation on the turbulence structure of supersonic boundary layers. J. Fluid Mech. 63 (3), 449–464.CrossRefGoogle Scholar
Bradshaw, P. 1977 Compressible turbulent shear layers. Annu. Rev. Fluid Mech. 9, 33–54.CrossRefGoogle Scholar
Bradshaw, P., Ferris, D. & Atwell, N. 1967 Calculation of boundary layer development using the turbulent energy equation. J. Fluid Mech. 28, 593–616.CrossRefGoogle Scholar
Bowersox, R. 2009 Extension of equilibrium turbulent heat flux models to high-speed shear flows. J. Fluid Mech. 633, 61–70.CrossRefGoogle Scholar
Clauser, F. H. 1956 The turbulent boundary layer. In Advanced Applied Mechanics, vol. 4, pp. 1–51. Academic.Google Scholar
Coles, D. 1956 The law of the wake in the turbulent boundary layer. J. Fluid Mech. 1, 191–226.CrossRefGoogle Scholar
Donovan, J., Spina, E. & Smits, A. 1994 The structure of a supersonic turbulent boundary layers subjected to concave surface curvature. J. Fluid Mech. 259, 1–24.CrossRefGoogle Scholar
Duan, L. & Martin, M. P. 2011 Direct numerical simulation of hypersonic turbulent boundary layers. Part IV: effect of high enthalpy. J. Fluid Mech. 684, 25–59.CrossRefGoogle Scholar
Dussauge, J. P. & Gaviglio, J. 1987 The rapid expansion of a supersonic turbulent flow: role of bulk dilatation. J. Fluid Mech. 174, 81–112.CrossRefGoogle Scholar
Ecker, T., Lowe, K. & Simpson, R. Novel laser Doppler acceleration measurements of particle lag through a shock wave, AIAA Paper 2012-0694, 2012.CrossRefGoogle Scholar
Ekoto, I., Bowersox, R., Beutner, T. & Goss, L. 2009 Response of supersonic turbulent boundary layers to local and global mechanical distortions. J. Fluid Mech. 630, 225–265.CrossRefGoogle Scholar
Elena, M., Lacharme, J. P. & Gaviglio, J. 1985 Comparison of hot-wire and laser Doppler anemometry methods in supersonic turbulent boundary layers. In Proc. Intl Symp. on Laser Anemometry, pp. 151–157 ASME.Google Scholar
Ganapathisubramani, B. 2007 Statistical properties of streamwise velocity in a supersonic turbulent boundary layer. Phys. Fluids 19.CrossRefGoogle Scholar
Ganapathisubramani, B. 2008 Statistical structure of momentum sources and sinks in the outer region of a turbulent boundary layer. J. Fluid Mech. 606, 225–237.CrossRefGoogle Scholar
Ganapathisubramani, B., Hutchins, N., Hambleton, W. T., Longmire, E. K. & Marusic, I. 2005 Investigation of large-scale coherence in a turbulent boundary layer using two-point correlations. J. Fluid Mech. 524, 57–80.CrossRefGoogle Scholar
Herrin, J. & Dutton, J. 1997 The turbulence structure of a reattaching axisymmetric compressible free shear layer. Phys. Fluids 9, 3502–3512.CrossRefGoogle Scholar
Hinze, J. 1975 Turbulence. McGraw-Hill.Google Scholar
Hopkins, E. 1972 Charts for predicting turbulent skin friction from the van Driest Method (II), NASA TN – D-6945, Washington DC.Google Scholar
Humble, R. A., Peltier, S. J. & Bowersox, R. D. W. 2012 Visualization of the structural response of a hypersonic turbulent boundary layer to convex curvature. Phys. Fluids 24 (10), 24–48.CrossRefGoogle Scholar
Innovative Scientific Solutions, Inc. 2005. dPIV, 32-bit PIV Analysis Code, Software Package, Version 2.1, Innovative Scientific Solutions, Inc., Dayton, OH.Google Scholar
Klebanoff, P. S. 1955 Characteristics of Turbulence in a Boundary Layer with Zero Pressure Gradient, NACA Rep. 1247.Google Scholar
Kline, S., Reynolds, W., Schraub, F. & Runstadler, P. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.CrossRefGoogle Scholar
Krogstad, P.-A. & Skare, P. E. 1995 Influence of a strong adverse pressure gradient on the turbulent structure in a boundary layer. Phys. Fluids 7, 2014–2024.CrossRefGoogle Scholar
Launder, B., Reece, G. & Rodi, W. 1975 Progress in the development of a Reynolds-stress turbulence closure. J. Fluid Mech. 68 (3), 537–566.CrossRefGoogle Scholar
Lewis, J., Gran, R. & Kubota, T. 1973 An experiment on the adiabatic compressible turbulent boundary layer in adverse and favourable pressure gradients. J. Fluid Mech. 51, 657–672.CrossRefGoogle Scholar
Lu, S. S. & Willmarth, W. W. 1973 Measurements of the structure of the Reynolds stress in a turbulent boundary layer. J. Fluid Mech. 60, 481–511.CrossRefGoogle Scholar
Luker, J., Bowersox, R. & Buter, T. 2000 Influence of curvature-driven favourable pressure gradient on supersonic turbulent boundary layer. AIAA J. 38 (8), 1351–1359.CrossRefGoogle Scholar
McDonald, H. 1968 The departure from equilibrium of turbulent boundary layers. Aeronaut. Q. XIX Pt. 1, 1–19.CrossRefGoogle Scholar
Mei, R. 1996 Velocity fidelity of flow tracer particles. Exp. Fluids 22, 1–13.CrossRefGoogle Scholar
Morkovin, M. 1961 Effects of compressibility on turbulent flows. In The Mechanics of Turbulence, pp. 367–380. Gordon and Breach Science.Google Scholar
Nagib, N. M & Chauhan, K. A. 2008 Variations of von Karman coefficient in canonical flows. Phys. Fluids 20, 101518.CrossRefGoogle Scholar
Nolan, K. P., Walsh, E. J. & McEligot, D. M. 2010 Quadrant analysis of a transitional boundary layer subject to free stream turbulence. J. Fluid Mech. 658, 310–335.CrossRefGoogle Scholar
Panigrahi, P. K., Schroeder, A. & Kompenhans, J. 2008 Turbulent structures and budgets behind permeable ribs. Exp. Therm. Fluid Sci. 32, 1011–1033.CrossRefGoogle Scholar
Pope, S. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Raffel, M., Willert, C., Wereley, S. & Kompenhans, J. 2007 Particle Image Velocimetry. Springer.CrossRefGoogle Scholar
Raupach, M. 1981 Conditional statistics of Reynolds stress in rough-wall and smooth-wall turbulent boundary layers. J. Fluid Mech. 108, 363–382.CrossRefGoogle Scholar
Ringuette, M., Bookey, P., Wyckham, C. & Smits, A. 2009 Experimental study of a Mach 3 compression ramp interaction at ${\mathit{Re}}_{\theta } = 2400$ . AIAA J. 47 (2).CrossRefGoogle Scholar
Ringuette, M., Wu, M. & Martin, P. 2008 Coherent structures in direct numerical simulation of turbulent boundary layers at Mach 3. J. Fluid Mech. 594, 59–69.CrossRefGoogle Scholar
Schetz, J. 1993 Boundary Layer Theory. Prentice Hall.Google Scholar
Schultz-Grunow, F. 1940 A new resistance law for smooth plates. Luftfahrtforschung 17, 239–246.Google Scholar
Smits, A. J. & Dussauge, J.-P. 2006 Turbulent Shear Layers in Supersonic Flow.Google Scholar
Spalding, D. B. 1961 A single formula for the law of the wall. J. Appl. Mech. 28, 455–457.CrossRefGoogle Scholar
Spina, E. F., Smits, A. J. & Robinson, S. 1994 The physics of supersonic turbulent boundary layers. Annu. Rev. Fluid Mech. 26, 287–319.CrossRefGoogle Scholar
Smits, A. J., Spina, E. F., Alving, A. E., Smith, R. W., Fernando, E. M. & Donovan, J. F. 1989 A comparison of the turbulence structure of subsonic and supersonic boundary layers. Phys. Fluids A 1 (11), 1865–1875.CrossRefGoogle Scholar
Townsend, A. 1961 Equilibrium layers and wall turbulence. J. Fluid Mech. 11, 97–120.CrossRefGoogle Scholar
TSI, Inc. 2003. Model 9306A Six-Jet Atomizer Instruction Manual, 1930099, Revision B. TSI, Inc., Shoreview, MN.Google Scholar
Van Driest, E. R. 1956 The problem with aerodynamic heating. Aeronaut. Engng Rev. 15, 26–41.Google Scholar
White, F. 2006 Viscous Fluid Flow, 3rd edn. McGraw-Hill.Google Scholar
Wilcox, D. 2000 Turbulence Modeling for CFD. DCW Industries.Google Scholar
Zagarola, M. V. & Smits, A. J. 1998 Mean-flow scaling of turbulent pipe flow. J. Fluid Mech. 373, 33–79.CrossRefGoogle Scholar