Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-02T20:07:22.075Z Has data issue: false hasContentIssue false
  • English
  • Français

Resonance characteristics of tides in branching channels

Published online by Cambridge University Press:  09 July 2013

Niels C. Alebregtse ,
H. E. de Swart  and
H. M. Schuttelaars
Niels C. Alebregtse*
Affiliation:
Institute for Marine and Atmospheric research Utrecht, Utrecht University, Princetonplein 5, 3584CC Utrecht, The Netherlands
H. E. de Swart
Affiliation:
Institute for Marine and Atmospheric research Utrecht, Utrecht University, Princetonplein 5, 3584CC Utrecht, The Netherlands
H. M. Schuttelaars
Affiliation:
Delft Institute of Applied Mathematics/Mathematical Physics, Delft University of Technology, Mekelweg 4, P.O.Box 5031, 2600 GA Delft, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Resonance characteristics of tidal waves in a network are investigated with the linearized, one-dimensional shallow water equations. The network comprises a semi-enclosed main channel with an adjacent secondary channel at an arbitrary position. Water motion is forced by a prescribed incoming wave at the entrance of the main channel. The model is used to compute the ratio of sea surface height amplitude in the presence and absence of the secondary channel. Relevance lies in the possible construction of secondary channels to reduce tidal range in the main channel. When 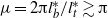$\mu = 2\mathrm{\pi} { l}_{b}^{\ast } / { l}_{t}^{\ast } \gtrsim \mathrm{\pi} $ (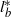${ l}_{b}^{\ast } $ being the length of the main channel, 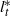${ l}_{t}^{\ast } $ the tidal wavelength) and friction is weak, it is found that reduction (amplification) of the tidal range occurs for secondary channels located less (more) than a quarter wavelength from the closed end of the main channel. Furthermore, a minimum is observed halfway between the closed end and the nodal point, and a maximum a quarter wavelength further seaward. With increasing friction and/or decreasing length of the main channel, amplitude ratios become less pronounced and depend weakly on the location of the secondary channel. The mechanism responsible for amplification or reduction of the sea surface height in the main channel is identified and explained in terms of the forced wave and waves radiating away from the secondary channel.

JFM classification

Geophysical and Geological Flows: Coastal engineering Geophysical and Geological Flows: Shallow water flows Waves/Free-surface Flows: Surface gravity waves
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 728 , 10 August 2013 , R3
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Buchwald, V. T. 1971 The diffraction of tides by a narrow channel. J. Fluid. Mech. 46 (3), 501–511.Google Scholar
Chernetsky, A. S., Schuttelaars, H. M. & Talke, S. A. 2010 The effect of tidal asymmetry and temporal settling lag on sediment trapping in estuaries. Ocean Dyn. 60, 1219–1241.CrossRefGoogle Scholar
Defant, A. 1961 Physical Oceanography, vol. 2. Pergamon.Google Scholar
Donner, M., Ladage, F., Stoschek, O. & Nguyen, H. 2012 Methods and analysis tools for redevelopments in an estuary with high suspended sediment concentrations. In Coastal Engineering (ed. Lynett, P. & McKee Smith, J.), vol. 1, p. 55. Coastal Engineering Research Council.Google Scholar
Garrett, C. 1975 Tides in gulfs. Deep-Sea Res. 22, 23–35.Google Scholar
de Jong, M. P. C. & Battjes, J. A. 2004 Low-frequency sea waves generated by atmospheric convection cells. J. Geophys. Res. 109, C01011.Google Scholar
Kinsler, L. E., Frey, A. R., Coppens, A. B. & Sanders, J. V. 2000 Fundamentals of Acoustics, 4th edn. John Wiley & Sons.Google Scholar
Lighthill, J. 1978 Waves in Fluids. Cambridge University Press.Google Scholar
Mei, C. C., Stiassnie, M. & Yue, D. K. P. 2005 Theory and Applications of Ocean Surface Waves: Linear Aspects, Advanced Series on Ocean Engineering, vol. 23. World Scientific.Google Scholar
Miles, J. W. 1971 Resonant response in harbours: an equivalent-circuit analysis. J. Fluid. Mech. 26 (2), 241–265.Google Scholar
Prandle, D. & Rahman, M. 1980 Tidal response in estuaries. J. Phys. Oceanogr. 10, 1552–1573.Google Scholar
Rainey, R. C. T. 2009 The optimum position for a tidal power barrage in Severn estuary. J. Fluid. Mech. 636, 497–507.Google Scholar
Schuttelaars, H. M., de Jonge, V. N. & Chernetsky, A. S. 2013 Improving the predictive power when modelling physical effects of human interventions in estuarine systems. Ocean Coast. Manage. 79, 70–82.CrossRefGoogle Scholar
Schuttelaars, H. M. & de Swart, H. E. 2000 Multiple morphodynamic equilibria in tidal embayments. J. Geophys. Res. 105 (C10), 24105–24118.Google Scholar
Zhong, L., Li, M. & Foreman, M. G. G. 2008 Resonance and sea level variability in Chesapeake Bay. Cont. Shelf Res. 28, 2565–2573.CrossRefGoogle Scholar
Zimmerman, J. T. F. 1992 On the Lorentz linearization of a nonlinearly damped tidal Helmholtz oscillator. Proc. Koninklijke Nederlandse Akademie van Wetenschappen 95 (1), 127–145.Google Scholar