Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Najjar, F. M.
2018.
Meso-scale simulations of shock-particle interactions in near-wall proximity.
Vol. 1979,
Issue. ,
p.
080009.
Zhang, Li-Te
Sui, Zhen-Zhen
and
Shi, Hong-Hui
2018.
Interaction of a shock wave with multiple spheres suspended in different arrangements.
Journal of Applied Physics,
Vol. 123,
Issue. 10,
Marjanovic, Goran
Hackl, Jason
Shringarpure, Mrugesh
Annamalai, Subramanian
Jackson, Thomas L.
and
Balachandar, S.
2018.
Inviscid simulations of expansion waves propagating into structured particle beds at low volume fractions.
Physical Review Fluids,
Vol. 3,
Issue. 9,
Prestridge, Kathy
2018.
Experimental adventures in variable-density mixing.
Physical Review Fluids,
Vol. 3,
Issue. 11,
Bordoloi, Ankur D
Ding, Liuyang
Martinez, Adam A
Prestridge, Katherine
and
Adrian, Ronald J
2018.
A new method to calculate unsteady particle kinematics and drag coefficient in a subsonic post-shock flow.
Measurement Science and Technology,
Vol. 29,
Issue. 7,
p.
074001.
Yin, Jingyue
Ding, Juchun
and
Luo, Xisheng
2018.
Numerical study on dusty shock reflection over a double wedge.
Physics of Fluids,
Vol. 30,
Issue. 1,
Middlebrooks, John B.
Avgoustopoulos, Constantine G.
Black, Wolfgang J.
Allen, Roy C.
and
McFarland, Jacob A.
2018.
Droplet and multiphase effects in a shock-driven hydrodynamic instability with reshock.
Experiments in Fluids,
Vol. 59,
Issue. 6,
Hughes, Kyle
Balachandar, S.
Kim, Nam H.
Park, Chanyoung
Haftka, Raphael
Diggs, Angela
Littrell, Donald M.
and
Darr, Jason
2018.
Forensic Uncertainty Quantification for Experiments on the Explosively Driven Motion of Particles.
Journal of Verification, Validation and Uncertainty Quantification,
Vol. 3,
Issue. 4,
Bordoloi, A.
Martinez, A.
and
Prestridge, K.
2019.
31st International Symposium on Shock Waves 2.
p.
681.
Sugiyama, Y.
Ando, H.
Shimura, K.
and
Matsuo, A.
2019.
Numerical investigation of the interaction between a shock wave and a particle cloud curtain using a CFD–DEM model.
Shock Waves,
Vol. 29,
Issue. 4,
p.
499.
Hughes, K. T.
Balachandar, S.
Diggs, A.
Haftka, R.
Kim, N. H.
and
Littrell, D.
2020.
Simulation-driven design of experiments examining the large-scale, explosive dispersal of particles.
Shock Waves,
Vol. 30,
Issue. 4,
p.
325.
Charonko, John J
Fratantonio, Dominique
Mayer, J Michael
Bordoloi, Ankur
and
Prestridge, Kathy P
2020.
Windowed Fourier transform and cross-correlation algorithms for molecular tagging velocimetry.
Measurement Science and Technology,
Vol. 31,
Issue. 7,
p.
074007.
Utkin, P. S.
Sidorenko, D. A.
and
Boiko, V. M.
2021.
Dynamics of motion of a pair of particles in a supersonic flow.
Shock Waves,
Vol. 31,
Issue. 6,
p.
571.
Hughes, K. T.
Charonko, J. J.
Prestridge, K. P.
Kim, N. H.
Haftka, R. T.
and
Balachandar, S.
2021.
Proton radiography of explosively dispersed metal particles with varying volume fraction and varying carrier phase.
Shock Waves,
Vol. 31,
Issue. 1,
p.
75.
Acharya, N.
Aluie, H.
and
Shang, J. K.
2022.
Numerical investigation of laser-driven shock interaction with a deformable particle.
Physics of Plasmas,
Vol. 29,
Issue. 5,
Wang, Yuan
and
Ge, Wei
2024.
Simulation of fluid‐structure interaction using the boundary data immersion method with adaptive mesh refinement.
International Journal for Numerical Methods in Fluids,
Vol. 96,
Issue. 7,
p.
1156.
Capecelatro, Jesse
and
Wagner, Justin L.
2024.
Gas–Particle Dynamics in High-Speed Flows.
Annual Review of Fluid Mechanics,
Vol. 56,
Issue. 1,
p.
379.
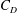 $C_{D}$) that are much higher than those predicted by quasi-steady and unsteady drag models. Nylon particles with mean diameter of
$C_{D}$) that are much higher than those predicted by quasi-steady and unsteady drag models. Nylon particles with mean diameter of 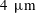 $4~\unicode[STIX]{x03BC}\text{m}$, accelerated by one-dimensional normal shocks (Mach number
$4~\unicode[STIX]{x03BC}\text{m}$, accelerated by one-dimensional normal shocks (Mach number 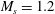 $M_{s}=1.2$, 1.3 and 1.4), have measured
$M_{s}=1.2$, 1.3 and 1.4), have measured 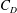 $C_{D}$ values that follow a power-law behaviour. The drag is a function of the time-dependent Knudsen number,
$C_{D}$ values that follow a power-law behaviour. The drag is a function of the time-dependent Knudsen number, 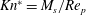 $Kn^{\ast }=M_{s}/Re_{p}$, where the particle Reynolds number (
$Kn^{\ast }=M_{s}/Re_{p}$, where the particle Reynolds number (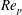 $Re_{p}$) is calculated using the time-dependent slip velocity. Some portion of the drag can be attributed to quasi-steady forces, but the total drag cannot be predicted by current unsteady force models that are based on the Basset–Boussinesq–Oseen equation and pressure drag. The largest contribution to the total drag is the unsteady component (
$Re_{p}$) is calculated using the time-dependent slip velocity. Some portion of the drag can be attributed to quasi-steady forces, but the total drag cannot be predicted by current unsteady force models that are based on the Basset–Boussinesq–Oseen equation and pressure drag. The largest contribution to the total drag is the unsteady component (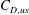 $C_{D,us}$) until the particle attains
$C_{D,us}$) until the particle attains 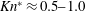 $Kn^{\ast }\approx 0.5{-}1.0$, then the unsteady contribution decays. The quasi-steady component (
$Kn^{\ast }\approx 0.5{-}1.0$, then the unsteady contribution decays. The quasi-steady component (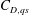 $C_{D,qs}$) increases almost linearly with
$C_{D,qs}$) increases almost linearly with 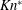 $Kn^{\ast }$, intersects the
$Kn^{\ast }$, intersects the 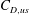 $C_{D,us}$ at
$C_{D,us}$ at 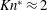 $Kn^{\ast }\approx 2$ and becomes the primary contributor to the drag towards the end of the relaxation zone as
$Kn^{\ast }\approx 2$ and becomes the primary contributor to the drag towards the end of the relaxation zone as 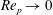 $Re_{p}\rightarrow 0$. There are currently no analytical models that are able to predict the nonlinear behaviour of the shock accelerated particles during the relaxation phase of the flow.
$Re_{p}\rightarrow 0$. There are currently no analytical models that are able to predict the nonlinear behaviour of the shock accelerated particles during the relaxation phase of the flow.