Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-12-01T04:05:46.915Z Has data issue: false hasContentIssue false
  • English
  • Français

Relationship between the heat transfer law and the scalar dissipation function in a turbulent channel flow

Published online by Cambridge University Press:  29 September 2017

Hiroyuki Abe Open the ORCID record for Hiroyuki Abe [Opens in a new window]  and
Robert Anthony Antonia
Hiroyuki Abe*
Affiliation:
Japan Aerospace Exploration Agency, Tokyo 182-8522, Japan
Robert Anthony Antonia
Affiliation:
Discipline of Mechanical Engineering, University of Newcastle, Newcastle, New South Wales 2308, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Integration across a fully developed turbulent channel flow of the transport equations for the mean and turbulent parts of the scalar dissipation rate yields relatively simple relations for the bulk mean scalar and wall heat transfer coefficient. These relations are tested using direct numerical simulation datasets obtained with two isothermal boundary conditions (constant heat flux and constant heating source) and a molecular Prandtl number Pr of 0.71. 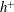A logarithmic dependence on the Kármán number $h^{+}$ is established for the integrated mean scalar in the range $h^{+}\geqslant 400$ where the mean part of the total scalar dissipation exhibits near constancy, whilst the integral of the turbulent scalar dissipation rate 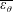$\overline{\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D703}}}$ increases logarithmically with 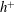$h^{+}$. This logarithmic dependence is similar to that established in a previous paper (Abe & Antonia, J. Fluid Mech., vol. 798, 2016, pp. 140–164) for the bulk mean velocity. However, the slope (2.18) for the integrated mean scalar is smaller than that (2.54) for the bulk mean velocity. The ratio of these two slopes is 0.85, which can be identified with the value of the turbulent Prandtl number in the overlap region. It is shown that the logarithmic 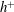$h^{+}$ increase of the integrated mean scalar is intrinsically associated with the overlap region of 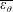$\overline{\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D703}}}$, established for 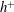$h^{+}$ (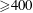${\geqslant}400$). The resulting heat transfer law also holds at a smaller 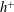$h^{+}$ (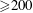${\geqslant}200$) than that derived by assuming a log law for the mean temperature.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 830 , 10 November 2017 , pp. 300 - 325
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H. & Antonia, R. A. 2009 Turbulent Prandtl number in a channel flow for Pr = 0. 025 and 0. 71. In Proceedings of the 6th International Symposium on Turbulence and Shear Flow Phenomena, Seoul, Korea (ed. Kasagi, N., Eaton, J. K., Friedrich, R., Humphrey, J. A. C., Johansson, A. V. & Sung, H. J.), vol. 1, pp. 67–72.Google Scholar
Abe, H. & Antonia, R. A. 2011 Scaling of normalized mean energy and scalar dissipation rates in a turbulent channel flow. Phys. Fluids 23, 055104.CrossRefGoogle Scholar
Abe, H. & Antonia, R. A. 2016 Relationship between the energy dissipation function and the skin friction law in a turbulent channel flow. J. Fluid Mech. 798, 140–164.Google Scholar
Abe, H., Antonia, R. A. & Kawamura, H. 2009 Correlation between small-scale velocity and scalar fluctuations in a turbulent channel flow. J. Fluid Mech. 627, 1–32.CrossRefGoogle Scholar
Abe, H., Kawamura, H. & Choi, H. 2004b Very large-scale structures and their effects on the wall shear-stress fluctuations in a turbulent channel flow up to Re 𝜏 = 640. Trans. ASME J. Fluids Engng 126, 835–843.CrossRefGoogle Scholar
Abe, H., Kawamura, H. & Matsuo, Y. 2001 Direct numerical simulation of a fully developed turbulent channel flow with respect to the Reynolds number dependence. Trans. ASME J. Fluids Engng 123, 382–393.Google Scholar
Abe, H., Kawamura, H. & Matsuo, Y. 2004a Surface heat-flux fluctuations in a turbulent channel flow up to Re 𝜏 = 1020 with Pr = 0. 025 and 0.71. Intl J. Heat Fluid Flow 25, 404–419.Google Scholar
Afzal, N. 1976 Millikan’s argument at moderately large Reynolds number. Phys. Fluids 19, 600–602.Google Scholar
Antonia, R. A., Abe, H. & Kawamura, H. 2009 Analogy between velocity and scalar fields in a turbulent channel flow. J. Fluid Mech. 628, 241–268.Google Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2014 Velocity statistics in turbulent channel flow up to Re 𝜏 = 4000. J. Fluid Mech. 742, 171–191.Google Scholar
Bradshaw, B. 1967 ‘Inactive’ motion and pressure fluctuations in turbulent boundary layers. J. Fluid Mech. 30, 241–258.CrossRefGoogle Scholar
Dean, R. B. 1978 Reynolds number dependence of skin friction and other bulk flow variables in two-dimensional rectangular duct flow. Trans. ASME J. Fluids Engng 100, 215–223.CrossRefGoogle Scholar
Djenidi, L. & Antonia, R. A. 2009 Momentum and heat transport in a three-dimensional transitional wake of a heated square cylinder. J. Fluid Mech. 640, 109–129.CrossRefGoogle Scholar
Guezennec, Y., Stretch, D. & Kim, J. 1990 The structure of turbulent channel flow with passive scalar transport. In Proceedings of the Summer Program 1990, pp. 127–138. Centre for Turbulence Research, Stanford University.Google Scholar
Hasegawa, Y. & Kasagi, N. 2011 Dissimilar control of momentum and heat transfer in a fully developed turbulent channel flow. J. Fluid Mech. 683, 57–93.Google Scholar
Horiuti, K. 1992 Assessment of two-equation models of turbulent passive-scalar diffusion in channel flow. J. Fluid Mech. 238, 405–433.Google Scholar
Hoyas, S. & Jiménez, J. 2008 Reynolds number effects on the Reynolds-stress budgets in turbulent channels. Phys. Fluids 20, 101511.Google Scholar
Johansson, A. V. & Wikström, P. M. 1999 DNS and modelling of passive scalar transport in turbulent channel flow with a focus on scalar dissipation rate modelling. Flow Turbul. Combust. 63, 223–245.Google Scholar
Kader, B. A. 1981 Temperature and concentration profiles in fully turbulent boundary layers. Intl J. Heat Mass Transfer 24, 1541–1544.Google Scholar
Kader, B. A. & Yaglom, A. M. 1972 Heat and mass transfer laws for fully turbulent wall flows. Intl. J. Heat Mass Transfer 15, 2329–2351.Google Scholar
Kaneda, Y., Morishita, K. & Ishihara, T. 2013 Small scale universality and spectral characteristics in turbulent flows. In Proceedings of the 8th International Symposium on Turbulence and Shear Flow Phenomena, Poitiers, France (INV2).Google Scholar
Kasagi, N., Tomita, Y. & Kuroda, A. 1992 Direct numerical simulation of passive scalar field in a turbulent channel flow. Trans. ASME J. Heat Transfer 144, 598–606.Google Scholar
Kawamura, H., Abe, H. & Matsuo, Y. 1999 DNS of turbulent heat transfer in channel flow with respect to Reynolds and Prandtl number effects. Intl J. Heat Fluid Flow 20, 196–207.CrossRefGoogle Scholar
Kays, W. M. 1966 Convective Heat and Mass Transfer. McGraw-Hill.Google Scholar
Kays, W. M. & Crawford, M. E. 1980 Convective Heat and Mass Transfer, 2nd edn. McGraw-Hill.Google Scholar
Kim, J. & Moin, P. 1989 Transport of passive scalars in a turbulent channel flow. In Turbulent Shear Flows (ed. André, J.-C., Cousteix, J., Durst, F., Launder, B. E., Schmidt, F. W. & Whitelaw, J. H.), vol. 6, pp. 85–96. Springer.CrossRefGoogle Scholar
Kong, H., Choi, H. & Lee, J. S. 2000 Direct numerical simulation of turbulent thermal boundary layers. Phys. Fluids 12, 2555–2568.Google Scholar
Kozuka, M., Seki, Y. & Kawamura, H. 2009 DNS of turbulent heat transfer in a channel flow with a high spatial resolution. Intl J. Heat Fluid Flow 30, 514–524.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 ≈ 5200. J. Fluid Mech. 774, 395–415.Google Scholar
Li, Q., Schlatter, P., Brandt, L. & Henningson, D. S. 2009 DNS of a spatially developing turbulent boundary layer with passive scalar transport. Intl J. Heat Fluid Flow 30, 916–929.Google Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Effect of the computational domain on direct simulations of turbulent channels up to Re 𝜏 = 4200. Phys. Fluids 26, 011702.CrossRefGoogle Scholar
Lyons, S. L., Hanratty, T. J. & McLaughlin, J. B. 1991 Direct numerical simulation of passive heat transfer in a turbulent channel flow. Intl J. Heat Mass Transfer 34, 1149–1161.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
McKeon, B. J. & Morrison, J. F. 2007 Asymptotic scaling in turbulent pipe flow. Phil. Trans. R. Soc. Lond. A 365, 771–787.Google Scholar
Monin, A. S. & Yaglom, A. M. 1971 Statistical Fluid Mechanics: Mechanics of Turbulence, vol. 1. MIT Press.Google Scholar
Monty, J. P.2005 Developments in smooth wall turbulent duct flows. PhD thesis, University of Melbourne, Australia.Google Scholar
Morinishi, Y., Lund, T. S., Vasilyev, O. V. & Moin, P. 1998 Fully conservative higher order finite difference schemes for incompressible flow. J. Comput. Phys. 143, 90–124.Google Scholar
Morinishi, Y., Tamano, S. & Nakamura, E. 2003 Numerical analysis of incompressible turbulent channel flow with different thermal wall boundary conditions. Trans. JSME B 69, 1313–1320; (in Japanese).Google Scholar
Na, Y., Papavassiliou, D. V. & Hanratty, T. J. 1999 Use of direct numerical simulation to study the effect of Prandtl number on temperature fields. Intl J. Heat Fluid Flow 20, 187–195.Google Scholar
Nagano, Y. & Kim, C. 1988 A two-equation model for heat transport in wall turbulent shear flows. Trans. ASME J. Heat Transfer 110, 583–589.Google Scholar
Nagano, Y. & Tagawa, M. 1988 Statistical characteristics of wall turbulence with a passive scalar. J. Fluid Mech. 196, 157–185.CrossRefGoogle Scholar
Ould-Rouiss, M., Bousbai, M. & Mazouz, A. 2013 Large eddy simulation of turbulent heat transfer in pipe flows with respect to Reynolds and Prandtl number effects. Acta Mechanica 224, 1133–1155.Google Scholar
Pirozzoli, S., Bernardini, M. & Orlandi, P. 2016 Passive scalars in turbulent channel flow at high Reynolds number. J. Fluid Mech. 788, 614–639.Google Scholar
Rogers, M. M., Mansour, N. N. & Reynolds, W. C. 1989 An algebraic model for the turbulent flux of a passive scalar. J. Fluid Mech. 203, 77–101.Google Scholar
Rotta, J. C. 1962 Turbulent boundary layers in incompressible flow. Prog. Aeronaut. Sci. 2, 1–219.Google Scholar
Saruwatari, S. & Yamamoto, Y. 2014 Prandtl number effect on near wall temperature profile in high-Reynolds number channel flows. Trans. JSME B 80 (814), 20p (in Japanese).Google Scholar
Seki, Y., Abe, H. & Kawamura, H. 2003 DNS of turbulent heat transfer in a channel flow with different thermal boundary conditions. In Proceedings of the 6th ASME-JSME Thermal Engineering Joint Conference, March 16–20, TED-AJ03-226.Google Scholar
Simpson, R. L., Whitten, D. G. & Moffat, R. J. 1970 An experimental study of the turbulent Prandtl number of air with injection and suction. Intl J. Heat Mass Transfer 13, 125–143.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Sreenivasan, K. R. 1995 The energy dissipation in turbulent shear flows. In Symposium on Developments in Fluid Dynamics and Aerospace Engineering (ed. Deshpande, S. M., Prabhu, A., Sreenivasan, K. R. & Viswanath, P. R.), pp. 159–190. Interline.Google Scholar
Subramanian, C. S. & Antonia, R. A. 1981 Effect of Reynolds number on a slightly heated turbulent boundary layer. Intl J. Heat Mass Transfer 24 (11), 1833–1846.Google Scholar
Teitel, M. & Antonia, R. A. 1993 Heat transfer in a fully developed turbulent channel flow: comparison between experiment and direct numerical simulations. Intl J. Heat Mass Transfer 36 (6), 1701–1706.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, vol. 2. Cambridge University Press.Google Scholar
Tsukahara, T., Iwamoto, K., Kawamura, H. & Takeda, T. 2006 DNS of heat transfer in a transitional channel flow accompanied by a turbulent puff-like structure. In Proceedings of Turbulence, Heat and Mass Transfer Conference 5, Dubrovnik, Croatia, pp. 193–196. Begell House.Google Scholar
Zanoun, E.-S., Durst, F. & Nagib, H. 2003 Evaluating the law of the wall in two-dimensional fully developed turbulent channel flows. Phys. Fluids 15, 3079–3089.Google Scholar
Zanoun, E.-S., Nagib, H. & Durst, F. 2009 Refined C f relation for turbulent channels and consequences for high Re experiments. Fluid Dyn. Res. 41, 1–12.Google Scholar