Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T18:47:05.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Regeneration of turbulent fluctuations in low-Froude-number flow over a sphere at a Reynolds number of 3700

Published online by Cambridge University Press:  08 September 2016

Anikesh Pal ,
Sutanu Sarkar ,
Antonio Posa  and
Elias Balaras
Anikesh Pal
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, CA 92093, USA
Sutanu Sarkar*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, CA 92093, USA
Antonio Posa
Affiliation:
Department of Mechanical and Aerospace Engineering, The George Washington University, DC 20052, USA
Elias Balaras
Affiliation:
Department of Mechanical and Aerospace Engineering, The George Washington University, DC 20052, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

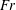Direct numerical simulations (DNS) are performed to study the behaviour of flow past a sphere in the regime of high stratification (low Froude number $Fr$). In contrast to previous results at lower Reynolds numbers, which suggest monotone suppression of turbulence with increasing stratification in flow past a sphere, it is found that, below a critical 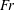$Fr$, increasing the stratification induces unsteady vortical motion and turbulent fluctuations in the near wake. The near wake is quantified by computing the energy spectra, the turbulence energy equation, the partition of energy into horizontal and vertical components, and the buoyancy Reynolds number. These diagnostics show that the stabilizing effect of buoyancy changes flow over the sphere to flow around the sphere. This qualitative change in the flow leads to a new regime of unsteady vortex shedding in the horizontal planes and intensified horizontal shear which result in turbulence regeneration.

JFM classification

Turbulent Flows: Stratified turbulence Turbulent Flows: Turbulent Flows Wakes/Jets: Wakes/Jets
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 804 , 10 October 2016 , R2
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arobone, E. & Sarkar, S. 2010 The statistical evolution of a stratified mixing layer with horizontal shear invoking feature extraction. Phys. Fluids 22, 1–15.Google Scholar
Balaras, E. 2004 Modeling complex boundaries using an external force field on fixed Cartesian grids in large-eddy simulations. Comput. Fluids 33 (3), 375–404.Google Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J. M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.Google Scholar
Brucker, K. A. & Sarkar, S. 2010 A comparative study of self-propelled and towed wakes in a stratified fluid. J. Fluid Mech. 652, 373–404.Google Scholar
Chomaz, J. M., Bonneton, P. & Hopfinger, E. J. 1993 The structure of the near wake of a sphere moving horizontally in a stratified fluid. J. Fluid Mech. 254, 1–21.CrossRefGoogle Scholar
Constantinescu, G. S. & Squires, K. D. 2003 LES and DES investigations of turbulent flow over a sphere at Re = 10 000. FTC 70 (1–4), 267–298.Google Scholar
Diamessis, P. J., Spedding, G. R. & Domaradzki, J. A. 2011 Similarity scaling and vorticity structure in high Reynolds number stably stratified turbulent wakes. J. Fluid Mech. 671, 52–95.Google Scholar
Hanazaki, H. 1988 A numerical study of three-dimensional stratified flow past a sphere. J. Fluid Mech. 192, 393–419.Google Scholar
Kim, H. J. & Durbin, P. A. 1988 Observations of the frequencies in a sphere wake and of drag increase by acoustic excitation. Phys. Fluids 31 (11), 3260–3265.Google Scholar
Lin, J. T. & Pao, Y. H. 1979 Wakes in stratified fluids. Annu. Rev. Fluid Mech. 11, 317–338.Google Scholar
Lin, Q., Lindberg, W. R., Boyer, D. L. & Fernando, H. J. S. 1992 Stratified flow past a sphere. J. Fluid Mech. 240, 315–354.Google Scholar
Lindborg, E. 2006 The energy cascade in a strongly stratified fluid. J. Fluid Mech. 550, 207–242.Google Scholar
Orr, T. S, Domaradzki, J. A., Spedding, G. R. & Constantinescu, G. S. 2015 Numerical simulations of the near wake of a sphere moving in a steady, horizontal motion through a linearly stratified fluid at Re = 1000. Phys. Fluids 27 (3), 035113.Google Scholar
Parnaudeau, P., Carlier, J., Heitz, D. & Lamballais, E. 2008 Experimental and numerical studies of the flow over a circular cylinder at Reynolds number 3900. Phys. Fluids 20 (8), 085101.Google Scholar
Riley, J. J. & deBruynKops, S. M. 2003 Dynamics of turbulence strongly influenced by buoyancy. Phys. Fluids 15 (7), 2047–2059.Google Scholar
Rodriguez, I., Borell, R., Lehmkuhl, O., Perez Segarra, C. D. & Oliva, A. 2011 Direct numerical simulation of the flow over a sphere at Re = 3700. J. Fluid Mech. 679, 263–287.Google Scholar
Sakamoto, H. & Haniu, H. 1990 A study on vortex shedding from spheres in a uniform flow. Trans. ASME J. Fluids Engng 112 (4), 386–392.CrossRefGoogle Scholar
Schlichting, H. 1979 Boundary Layer Theory, 7th edn. McGraw-Hill.Google Scholar
Seidl, V., Muzaferija, S. & Perić, M. 1997 Parallel DNS with local grid refinement. Appl. Sci. Res. 59 (4), 379–394.CrossRefGoogle Scholar
Spedding, G. R. 2014 Wake signature detection. Annu. Rev. Fluid Mech. 46, 273–302.Google Scholar
Tomboulides, A. G. & Orszag, S. A. 2000 Numerical investigation of transitional and weak turbulent flow past a sphere. J. Fluid Mech. 416, 45–73.Google Scholar
Yang, J. & Balaras, E. 2006 An embedded-boundary formulation for large-eddy simulation of turbulent flows interacting with moving boundaries. J. Comput. Phys. 215 (1), 12–40.Google Scholar
Yun, G., Kim, D. & Choi, H. 2006 Vortical structures behind a sphere at subcritical Reynolds numbers. Phys. Fluids 18 (1), 105102.Google Scholar